Question Number 114808 by mnjuly1970 last updated on 21/Sep/20
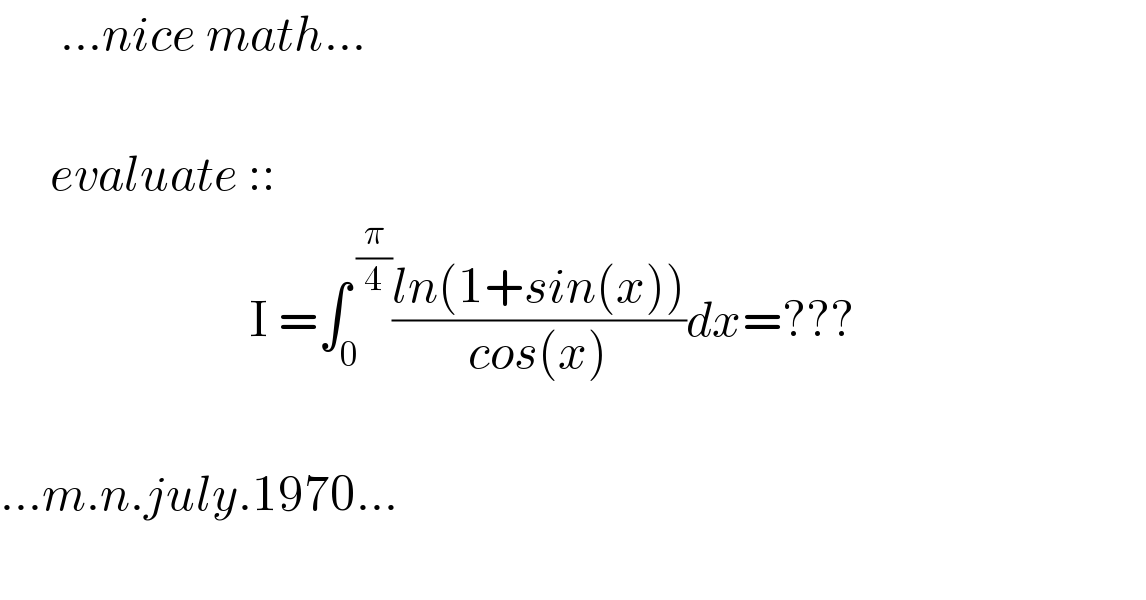
$$\:\:\:\:\:\:…{nice}\:{math}… \\ $$$$ \\ $$$$\:\:\:\:\:{evaluate}\::: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \frac{{ln}\left(\mathrm{1}+{sin}\left({x}\right)\right)}{{cos}\left({x}\right)}{dx}=???\: \\ $$$$ \\ $$$$…{m}.{n}.{july}.\mathrm{1970}… \\ $$$$\: \\ $$
Answered by mathdave last updated on 22/Sep/20
![solution let I=∫_0 ^(π/4) ((ln(1+sinx))/(cosx))dx=∫_0 ^(π/4) ((ln(1+sinx))/(1−sin^2 x))cosxdx put y=sinx I=∫_0 ^(1/( (√2))) ((ln(1+y))/(1−y^2 ))dy=(1/2)(∫_0 ^(1/( (√2))) ((ln(1+y))/(1−y))dy+∫_0 ^(1/( (√2))) ((ln(1+y))/(1+y))dy)=(1/2)(A+B) put y=1−2x in A let A=∫_((1/2)−((√2)/4)) ^(1/( (√2))) ((ln(2−2x))/x)dx=∫_((1/2)−((√2)/4)) ^(1/2) (((ln(1−x))/x)+((ln2)/x))dx A=∫_((1/2)−((√2)/4)) ^(1/2) ((ln(1−x))/x)dx+ln2∫_((1/2)−((√2)/4)) ^(1/2) (1/x)dx A=[−Li_2 (x)]_((1/2)−((√2)/4)) ^(1/2) +ln2[lnx]_((1/2)−((√2)/4)) ^(1/2) A=−Li_2 ((1/2))+Li_2 ((1/2)−((√2)/4))+ln2[ln((1/2))−ln((1/2)−((√2)/4))] A=−ln^2 (2)−Li_2 ((1/2))+Li_2 ((1/2)−((√2)/4))−ln2ln(2−(√2))+2ln^2 (2) A=(3/2)ln^2 (2)−(π^2 /(12))+Li_2 ((1/2)−((√2)/4))−ln2ln(2−(√2)).....(1) and B=∫_0 ^(1/( (√2))) ((ln(1+y))/(1+y))dy using IBP B=ln^2 (1+y)∣_0 ^(1/( (√2))) −∫_0 ^(1/( (√2))) ((ln(1+y))/(1+y))dy B=(1/2)ln^2 (1+(1/( (√2))))=(1/2)ln^2 (((2+(√2))/2))=(1/2)[ln(((2+(√2))/2))]^2 B=(1/2)[ln(2+(√2))−ln2]^2 B=(1/2)ln^2 (2+(√2))+(1/2)ln^2 (2)−ln2ln(2+(√2))....(2) but I=(1/2)(A+B) I=(1/2)((3/2)ln^2 (2)−(π^2 /(12))+Li_2 ((1/2)−((√2)/4))−ln2ln(2−(√2))+(1/2)ln^2 (2+(√2))−ln2ln(2+(√2))+(1/2)ln^2 (2)) I=(1/2)(2ln^2 (2)−(π^2 /(12))+Li_2 ((1/2)−((√2)/4))−ln2[ln(2−(√2))+ln(2+(√2))]+(1/2)ln^2 (2+(√2))) I=(1/2)(2ln^2 (2)−(π^2 /(12))+Li_2 ((1/2)−((√2)/4))−ln^2 (2)+(1/2)ln^2 (2+(√2))) I=(1/2)Li_2 ((1/2)−((√2)/4))−(π^2 /(24))+(1/4)ln^2 (2+(√2))+(1/2)ln^2 (2) ∵∫_0 ^(π/4) ((ln(1+sinx))/(cosx))dx=(1/2)Li_2 ((1/2)−((√2)/4))−(π^2 /(24))+(1/4)ln^2 (2+(√2))+(1/2)ln^2 (2) by mathdave(22/09/2020)](https://www.tinkutara.com/question/Q114929.png)
$${solution} \\ $$$${let} \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{sin}{x}\right)}{\mathrm{cos}{x}}{dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{sin}{x}\right)}{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} {x}}\mathrm{cos}{xdx} \\ $$$${put}\:{y}=\mathrm{sin}{x} \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \frac{\mathrm{ln}\left(\mathrm{1}+{y}\right)}{\mathrm{1}−{y}^{\mathrm{2}} }{dy}=\frac{\mathrm{1}}{\mathrm{2}}\left(\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \frac{\mathrm{ln}\left(\mathrm{1}+{y}\right)}{\mathrm{1}−{y}}{dy}+\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \frac{\mathrm{ln}\left(\mathrm{1}+{y}\right)}{\mathrm{1}+{y}}{dy}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({A}+{B}\right) \\ $$$${put}\:{y}=\mathrm{1}−\mathrm{2}{x}\:{in}\:\:{A} \\ $$$${let} \\ $$$${A}=\int_{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \frac{\mathrm{ln}\left(\mathrm{2}−\mathrm{2}{x}\right)}{{x}}{dx}=\int_{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\frac{\mathrm{ln}\left(\mathrm{1}−{x}\right)}{{x}}+\frac{\mathrm{ln2}}{{x}}\right){dx} \\ $$$${A}=\int_{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{\mathrm{ln}\left(\mathrm{1}−{x}\right)}{{x}}{dx}+\mathrm{ln2}\int_{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{\mathrm{1}}{{x}}{dx} \\ $$$${A}=\left[−{Li}_{\mathrm{2}} \left({x}\right)\right]_{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} +\mathrm{ln2}\left[\mathrm{ln}{x}\right]_{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$${A}=−{Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)+{Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\right)+\mathrm{ln2}\left[\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\right)\right] \\ $$$${A}=−\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)−{Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)+{Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\right)−\mathrm{ln2ln}\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)+\mathrm{2ln}^{\mathrm{2}} \left(\mathrm{2}\right) \\ $$$${A}=\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}+{Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\right)−\mathrm{ln2ln}\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)…..\left(\mathrm{1}\right)\:{and} \\ $$$${B}=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \frac{\mathrm{ln}\left(\mathrm{1}+{y}\right)}{\mathrm{1}+{y}}{dy}\:\:\:{using}\:{IBP} \\ $$$${B}=\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+{y}\right)\mid_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} −\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \frac{\mathrm{ln}\left(\mathrm{1}+{y}\right)}{\mathrm{1}+{y}}{dy} \\ $$$${B}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{ln}\left(\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{2}}\right)\right]^{\mathrm{2}} \\ $$$${B}=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{ln}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)−\mathrm{ln2}\right]^{\mathrm{2}} \\ $$$${B}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}+\sqrt{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\mathrm{ln2ln}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)….\left(\mathrm{2}\right) \\ $$$${but}\:{I}=\frac{\mathrm{1}}{\mathrm{2}}\left({A}+{B}\right) \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}+{Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\right)−\mathrm{ln2ln}\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}+\sqrt{\mathrm{2}}\right)−\mathrm{ln2ln}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)\right) \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}+{Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\right)−\mathrm{ln2}\left[\mathrm{ln}\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)+\mathrm{ln}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)\right]+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}+\sqrt{\mathrm{2}}\right)\right) \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}+{Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\right)−\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}+\sqrt{\mathrm{2}}\right)\right) \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}{Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{24}}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}+\sqrt{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right) \\ $$$$\because\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{sin}{x}\right)}{\mathrm{cos}{x}}{dx}=\frac{\mathrm{1}}{\mathrm{2}}{Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{24}}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}+\sqrt{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right) \\ $$$${by}\:{mathdave}\left(\mathrm{22}/\mathrm{09}/\mathrm{2020}\right) \\ $$
Commented by mnjuly1970 last updated on 22/Sep/20
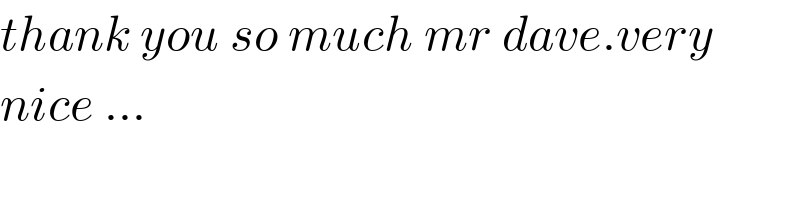
$${thank}\:{you}\:{so}\:{much}\:{mr}\:{dave}.{very} \\ $$$${nice}\:… \\ $$
Commented by Tawa11 last updated on 06/Sep/21

$$\mathrm{great}\:\mathrm{sir} \\ $$
