Question Number 115705 by mnjuly1970 last updated on 27/Sep/20
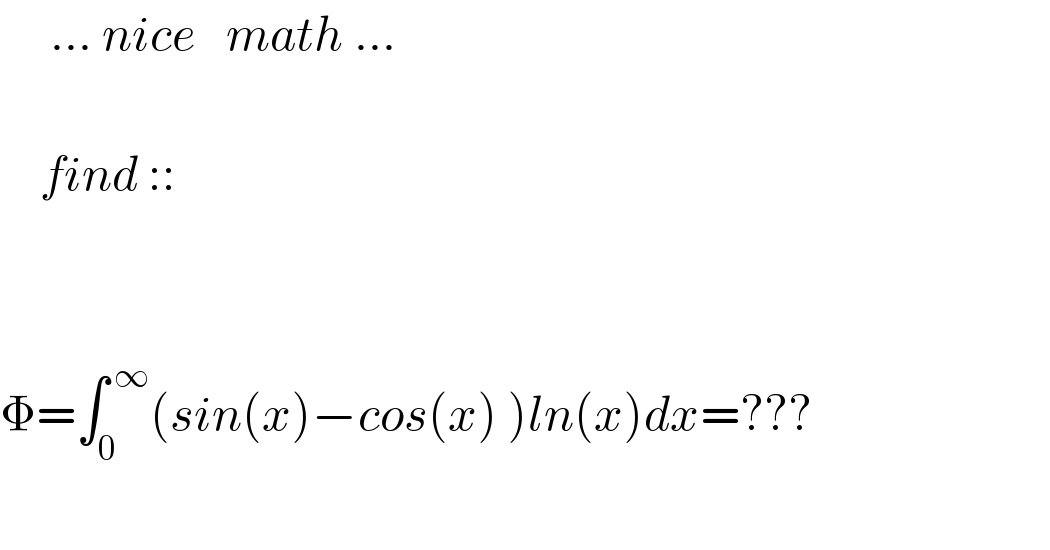
$$\:\:\:\:\:…\:{nice}\:\:\:{math}\:… \\ $$$$ \\ $$$$\:\:\:\:{find}\::: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\Phi=\int_{\mathrm{0}} ^{\:\infty} \left({sin}\left({x}\right)−{cos}\left({x}\right)\:\right){ln}\left({x}\right){dx}=??? \\ $$$$ \\ $$
Answered by Ar Brandon last updated on 28/Sep/20
![Φ=∫_0 ^∞ (sinx−cosx)lnxdx =−[(cosx+sinx)lnx]_0 ^∞ +∫_0 ^∞ [((sinx)/x)+((cosx)/x)]dx =−[(cosx+sinx)lnx]_0 ^∞ +(π/2)+∫_0 ^∞ ((cosx)/x)dx ...](https://www.tinkutara.com/question/Q115720.png)
$$\Phi=\int_{\mathrm{0}} ^{\infty} \left(\mathrm{sin}{x}−\mathrm{cos}{x}\right)\mathrm{ln}{x}\mathrm{d}{x} \\ $$$$\:\:\:\:=−\left[\left(\mathrm{cos}{x}+\mathrm{sin}{x}\right)\mathrm{ln}{x}\right]_{\mathrm{0}} ^{\infty} +\int_{\mathrm{0}} ^{\infty} \left[\frac{\mathrm{sin}{x}}{{x}}+\frac{\mathrm{cos}{x}}{{x}}\right]\mathrm{d}{x} \\ $$$$\:\:\:\:=−\left[\left(\mathrm{cos}{x}+\mathrm{sin}{x}\right)\mathrm{ln}{x}\right]_{\mathrm{0}} ^{\infty} +\frac{\pi}{\mathrm{2}}+\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{cos}{x}}{{x}}\mathrm{d}{x} \\ $$$$… \\ $$
Commented by Olaf last updated on 28/Sep/20
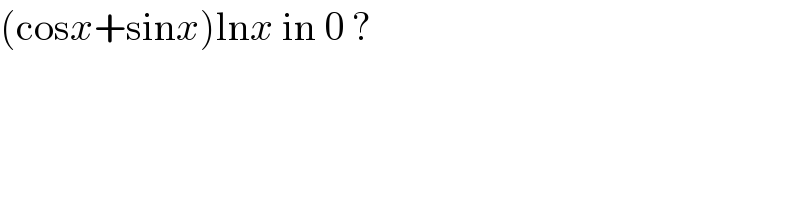
$$\left(\mathrm{cos}{x}+\mathrm{sin}{x}\right)\mathrm{ln}{x}\:\mathrm{in}\:\mathrm{0}\:? \\ $$
Commented by mnjuly1970 last updated on 28/Sep/20
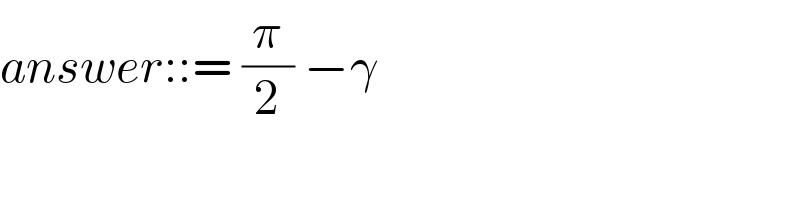
$${answer}::=\:\frac{\pi}{\mathrm{2}}\:−\gamma\: \\ $$
Commented by Ar Brandon last updated on 28/Sep/20
I haven't yet studied that Sir. This is also because I haven't found any Ebook on this. Do you any suggestions for me, please ?��
Commented by mnjuly1970 last updated on 28/Sep/20
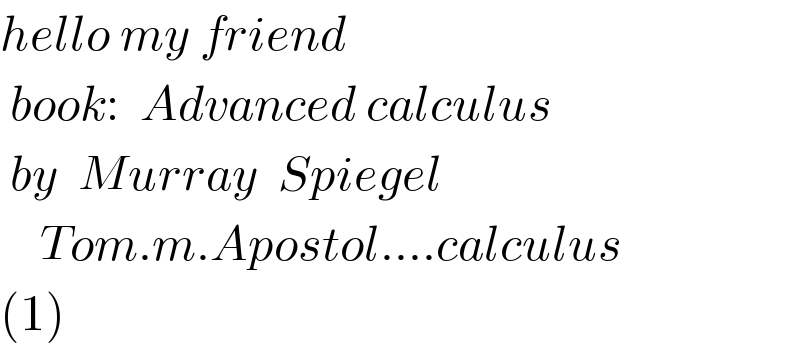
$${hello}\:{my}\:{friend} \\ $$$$\:{book}:\:\:{Advanced}\:{calculus}\: \\ $$$$\:{by}\:\:{Murray}\:\:{Spiegel} \\ $$$$\:\:\:\:{Tom}.{m}.{Apostol}….{calculus} \\ $$$$\left(\mathrm{1}\right) \\ $$
Commented by Ar Brandon last updated on 28/Sep/20
Thanks very much Sir.
