Question Number 115302 by mnjuly1970 last updated on 24/Sep/20
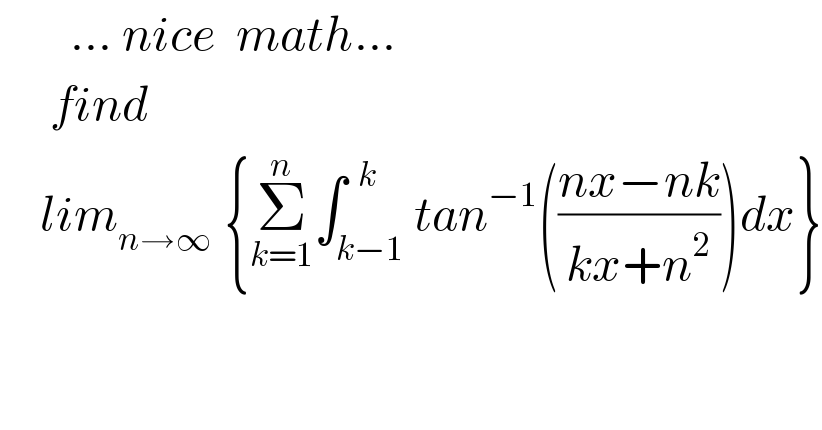
$$\:\:\:\:\:\:\:…\:{nice}\:\:{math}… \\ $$$$\:\:\:\:\:{find} \\ $$$$\:\:\:\:{lim}_{{n}\rightarrow\infty\:\:} \left\{\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\int_{{k}−\mathrm{1}} ^{\:\:{k}} {tan}^{−\mathrm{1}} \left(\frac{{nx}−{nk}}{{kx}+{n}^{\mathrm{2}} }\right){dx}\right\} \\ $$$$\: \\ $$
Answered by Olaf last updated on 24/Sep/20
![arctana−arctanb = arctan(((a−b)/(1+ab))) Let a = (x/n) and b = (k/n) arctan(x/n)−arctan(k/n) = arctan((((x/n)−(k/n))/(1+((xk)/n^2 )))) arctan(x/n)−arctan(k/n) = arctan(((nx−nk)/(kx+n^2 ))) I_k (x) = ∫_(k−1) ^k arctan(((nx−nk)/(kx+n^2 )))dx I_k (x) = ∫_(k−1) ^k [arctan((x/n))−arctan((k/n))]dx I_k (x) = [xarctan((x/n))]_(k−1) ^k ... −∫_(k−1) ^k x((1/n)/(1+((x/n))^2 ))dx−arctan(k/n) I_k (x) = karctan(k/n)−(k−1)arctan(((k−1)/n))... −[(1/2)ln(1+((x/n))^2 )]_(k−1) ^k −arctan(k/n) I_k (x) = karctan(k/n)−(k−1)arctan(((k−1)/n))... −(1/2)ln((1+((k/n))^2 )/(1+(((k−1)/n))^2 ))−arctan(k/n) Σ_(k=1) ^n I_k (x) = narctan(1)−(1/2)ln2−Σ_(k=1) ^n arctan((k/n)) Σ_(k=1) ^n I_k (x) = (π/4)n−(1/2)ln2−Σ_(k=1) ^n arctan((k/n)) to be continued...](https://www.tinkutara.com/question/Q115307.png)
$$\mathrm{arctan}{a}−\mathrm{arctan}{b}\:=\:\mathrm{arctan}\left(\frac{{a}−{b}}{\mathrm{1}+{ab}}\right) \\ $$$$\mathrm{Let}\:{a}\:=\:\frac{{x}}{{n}}\:\mathrm{and}\:{b}\:=\:\frac{{k}}{{n}} \\ $$$$\mathrm{arctan}\frac{{x}}{{n}}−\mathrm{arctan}\frac{{k}}{{n}}\:=\:\mathrm{arctan}\left(\frac{\frac{{x}}{{n}}−\frac{{k}}{{n}}}{\mathrm{1}+\frac{{xk}}{{n}^{\mathrm{2}} }}\right) \\ $$$$\mathrm{arctan}\frac{{x}}{{n}}−\mathrm{arctan}\frac{{k}}{{n}}\:=\:\mathrm{arctan}\left(\frac{{nx}−{nk}}{{kx}+{n}^{\mathrm{2}} }\right) \\ $$$$\mathrm{I}_{{k}} \left({x}\right)\:=\:\int_{{k}−\mathrm{1}} ^{{k}} \mathrm{arctan}\left(\frac{{nx}−{nk}}{{kx}+{n}^{\mathrm{2}} }\right){dx} \\ $$$$\mathrm{I}_{{k}} \left({x}\right)\:=\:\int_{{k}−\mathrm{1}} ^{{k}} \left[\mathrm{arct}{an}\left(\frac{{x}}{{n}}\right)−\mathrm{arctan}\left(\frac{{k}}{{n}}\right)\right]{dx} \\ $$$$\mathrm{I}_{{k}} \left({x}\right)\:=\:\left[{x}\mathrm{arct}{an}\left(\frac{{x}}{{n}}\right)\right]_{{k}−\mathrm{1}} ^{{k}} … \\ $$$$−\int_{{k}−\mathrm{1}} ^{{k}} {x}\frac{\frac{\mathrm{1}}{{n}}}{\mathrm{1}+\left(\frac{{x}}{{n}}\right)^{\mathrm{2}} }{dx}−\mathrm{arctan}\frac{{k}}{{n}} \\ $$$$\mathrm{I}_{{k}} \left({x}\right)\:=\:{k}\mathrm{arct}{an}\frac{{k}}{{n}}−\left({k}−\mathrm{1}\right)\mathrm{arctan}\left(\frac{{k}−\mathrm{1}}{{n}}\right)… \\ $$$$−\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\left(\frac{{x}}{{n}}\right)^{\mathrm{2}} \right)\right]_{{k}−\mathrm{1}} ^{{k}} −\mathrm{arctan}\frac{{k}}{{n}} \\ $$$$\mathrm{I}_{{k}} \left({x}\right)\:=\:{k}\mathrm{arctan}\frac{{k}}{{n}}−\left({k}−\mathrm{1}\right)\mathrm{arctan}\left(\frac{{k}−\mathrm{1}}{{n}}\right)… \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\frac{\mathrm{1}+\left(\frac{{k}}{{n}}\right)^{\mathrm{2}} }{\mathrm{1}+\left(\frac{{k}−\mathrm{1}}{{n}}\right)^{\mathrm{2}} }−\mathrm{arctan}\frac{{k}}{{n}} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{I}_{{k}} \left({x}\right)\:=\:{n}\mathrm{arctan}\left(\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln2}−\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{arctan}\left(\frac{{k}}{{n}}\right) \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{I}_{{k}} \left({x}\right)\:=\:\frac{\pi}{\mathrm{4}}{n}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln2}−\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{arctan}\left(\frac{{k}}{{n}}\right) \\ $$$${to}\:{be}\:{continued}… \\ $$$$ \\ $$
