Question Number 115000 by mnjuly1970 last updated on 22/Sep/20
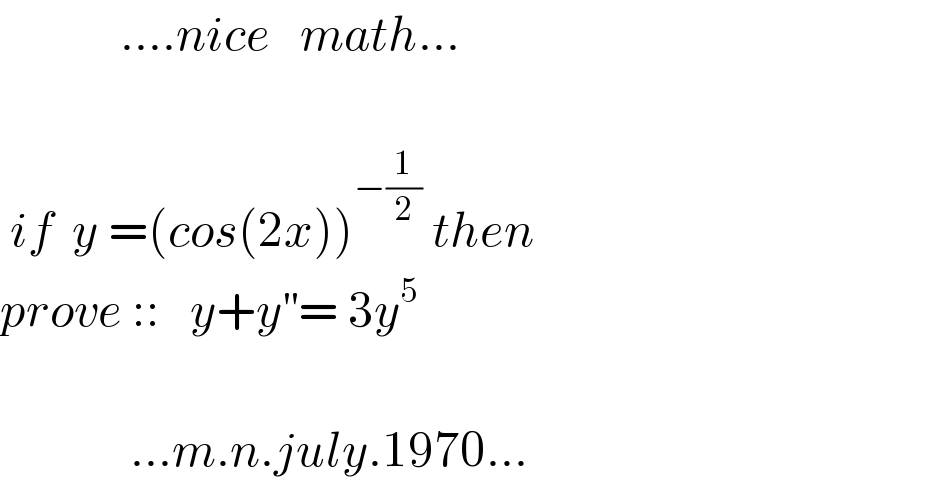
$$\:\:\:\:\:\:\:\:\:\:\:\:….{nice}\:\:\:{math}… \\ $$$$ \\ $$$$\:{if}\:\:{y}\:=\left({cos}\left(\mathrm{2}{x}\right)\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:{then} \\ $$$${prove}\:::\:\:\:{y}+{y}^{''} =\:\mathrm{3}{y}^{\mathrm{5}} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:…{m}.{n}.{july}.\mathrm{1970}… \\ $$
Answered by Dwaipayan Shikari last updated on 22/Sep/20
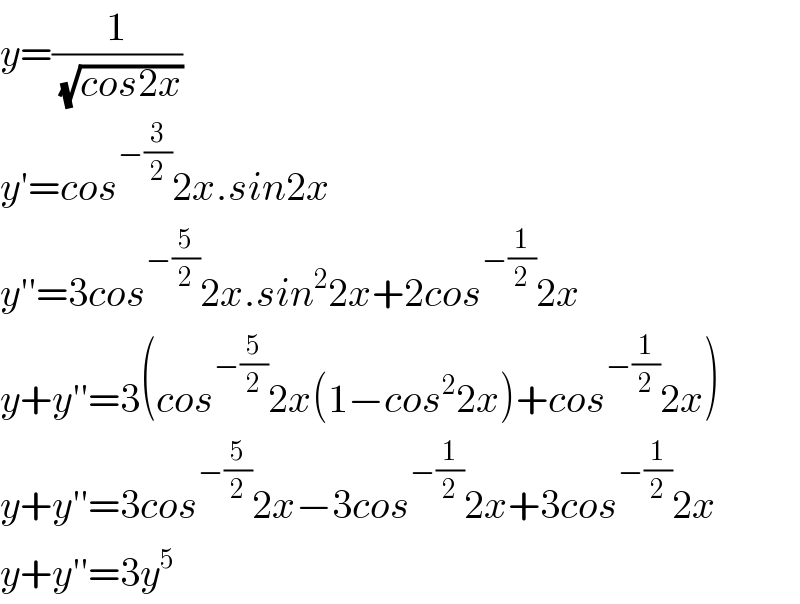
$${y}=\frac{\mathrm{1}}{\:\sqrt{{cos}\mathrm{2}{x}}} \\ $$$${y}'={cos}^{−\frac{\mathrm{3}}{\mathrm{2}}} \mathrm{2}{x}.{sin}\mathrm{2}{x} \\ $$$${y}''=\mathrm{3}{cos}^{−\frac{\mathrm{5}}{\mathrm{2}}} \mathrm{2}{x}.{sin}^{\mathrm{2}} \mathrm{2}{x}+\mathrm{2}{cos}^{−\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{2}{x} \\ $$$${y}+{y}''=\mathrm{3}\left({cos}^{−\frac{\mathrm{5}}{\mathrm{2}}} \mathrm{2}{x}\left(\mathrm{1}−{cos}^{\mathrm{2}} \mathrm{2}{x}\right)+{cos}^{−\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{2}{x}\right) \\ $$$${y}+{y}''=\mathrm{3}{cos}^{−\frac{\mathrm{5}}{\mathrm{2}}} \mathrm{2}{x}−\mathrm{3}{cos}^{−\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{2}{x}+\mathrm{3}{cos}^{−\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{2}{x} \\ $$$${y}+{y}''=\mathrm{3}{y}^{\mathrm{5}} \\ $$
Commented by mnjuly1970 last updated on 22/Sep/20
$${very}\:{nice}\:{very}\:{nice}\:…{thank} \\ $$$${you}\:{sir}… \\ $$
Commented by Canovas last updated on 29/Sep/20

$${Correct} \\ $$
Answered by $@y@m last updated on 23/Sep/20
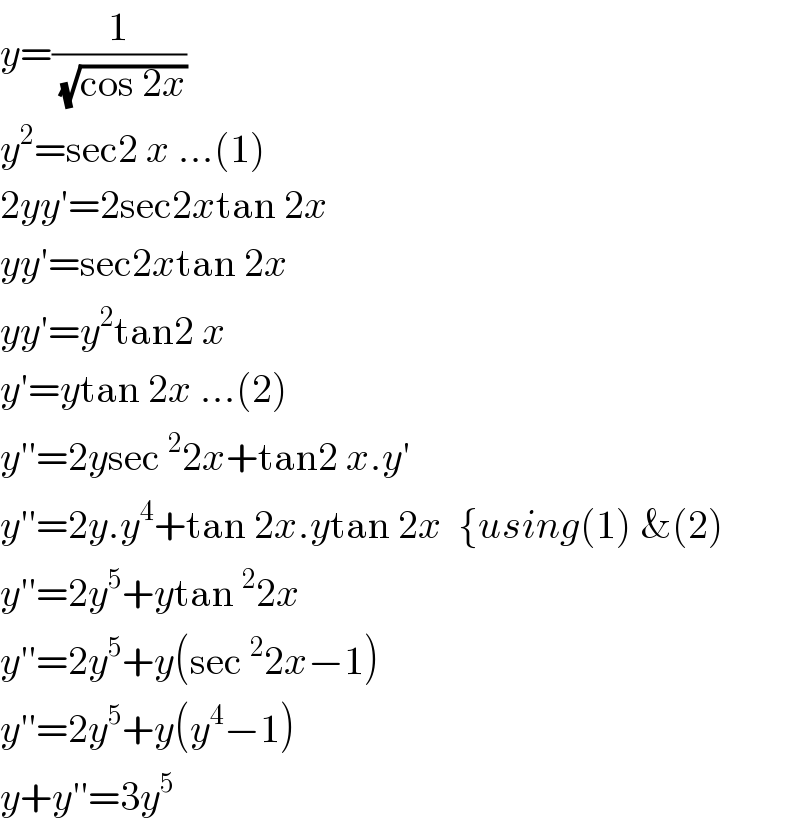
$${y}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{cos}\:\mathrm{2}{x}}}\:\:\: \\ $$$${y}^{\mathrm{2}} =\mathrm{sec2}\:{x}\:…\left(\mathrm{1}\right) \\ $$$$\mathrm{2}{yy}'=\mathrm{2sec2}{x}\mathrm{tan}\:\mathrm{2}{x} \\ $$$${yy}'=\mathrm{sec2}{x}\mathrm{tan}\:\mathrm{2}{x} \\ $$$${yy}'={y}^{\mathrm{2}} \mathrm{tan2}\:{x} \\ $$$${y}'={y}\mathrm{tan}\:\mathrm{2}{x}\:…\left(\mathrm{2}\right) \\ $$$${y}''=\mathrm{2}{y}\mathrm{sec}\:^{\mathrm{2}} \mathrm{2}{x}+\mathrm{tan2}\:{x}.{y}' \\ $$$${y}''=\mathrm{2}{y}.{y}^{\mathrm{4}} +\mathrm{tan}\:\mathrm{2}{x}.{y}\mathrm{tan}\:\mathrm{2}{x}\:\:\left\{{using}\left(\mathrm{1}\right)\:\&\left(\mathrm{2}\right)\right. \\ $$$${y}''=\mathrm{2}{y}^{\mathrm{5}} +{y}\mathrm{tan}\:^{\mathrm{2}} \mathrm{2}{x} \\ $$$${y}''=\mathrm{2}{y}^{\mathrm{5}} +{y}\left(\mathrm{sec}\:^{\mathrm{2}} \mathrm{2}{x}−\mathrm{1}\right) \\ $$$${y}''=\mathrm{2}{y}^{\mathrm{5}} +{y}\left({y}^{\mathrm{4}} −\mathrm{1}\right) \\ $$$${y}+{y}''=\mathrm{3}{y}^{\mathrm{5}} \\ $$
Commented by mnjuly1970 last updated on 23/Sep/20
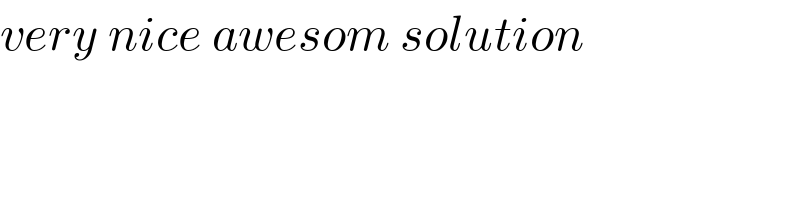
$${very}\:{nice}\:{awesom}\:{solution} \\ $$$$ \\ $$
