Question Number 115222 by mnjuly1970 last updated on 24/Sep/20
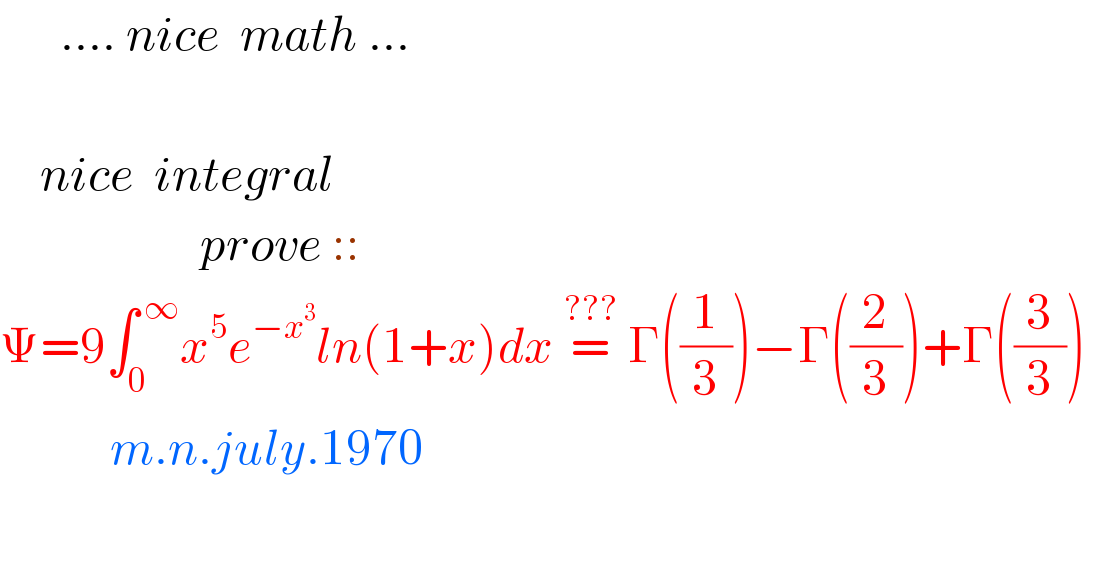
$$\:\:\:\:\:\:….\:{nice}\:\:{math}\:… \\ $$$$ \\ $$$$\:\:\:\:{nice}\:\:{integral}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{prove}\::: \\ $$$$\Psi=\mathrm{9}\int_{\mathrm{0}} ^{\:\infty} {x}^{\mathrm{5}} {e}^{−{x}^{\mathrm{3}} } {ln}\left(\mathrm{1}+{x}\right){dx}\:\overset{???} {=}\:\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)−\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right)+\Gamma\left(\frac{\mathrm{3}}{\mathrm{3}}\right)\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{m}.{n}.{july}.\mathrm{1970} \\ $$$$\:\: \\ $$
Answered by mathdave last updated on 24/Sep/20
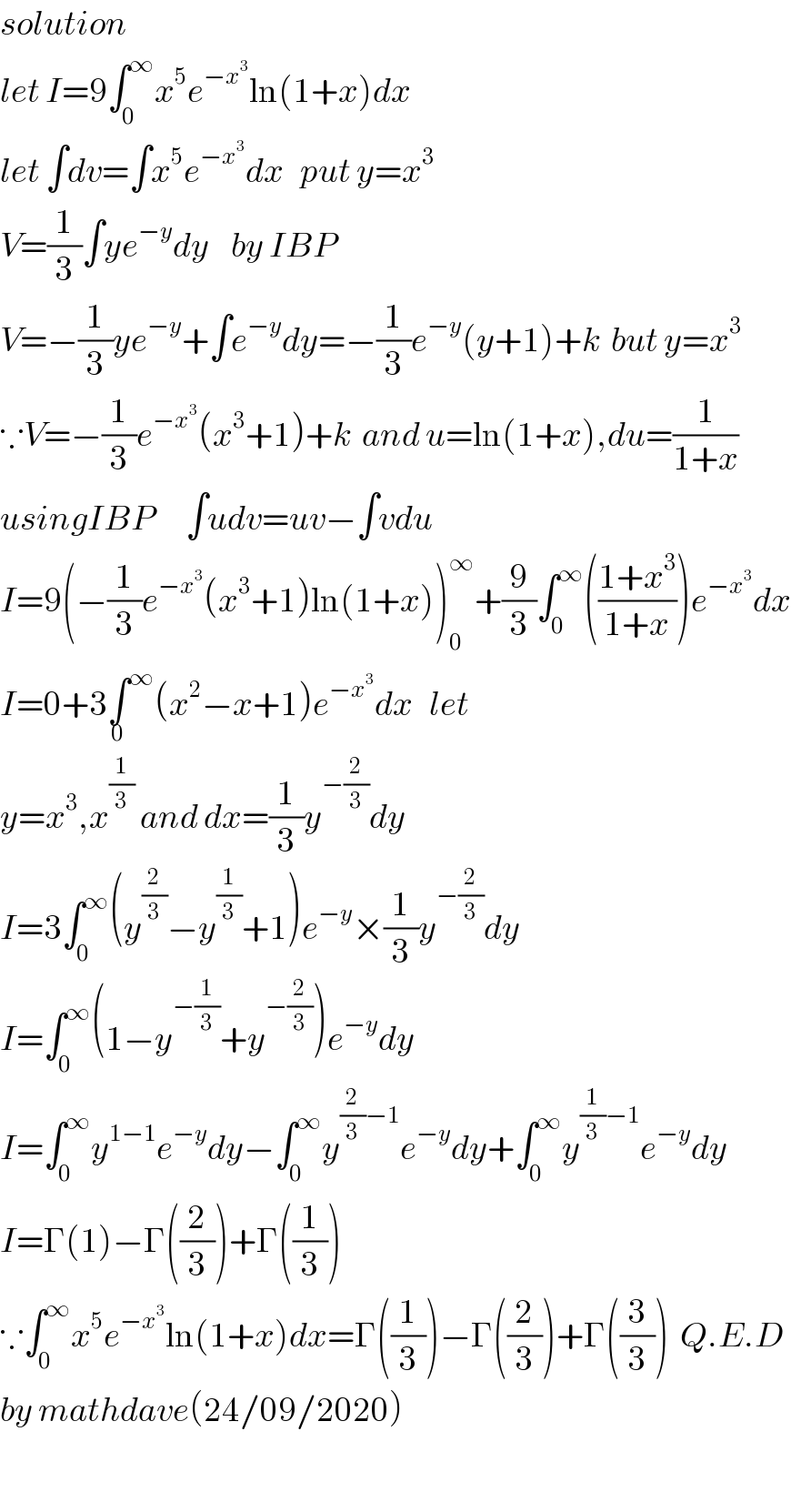
$${solution}\: \\ $$$${let}\:{I}=\mathrm{9}\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{5}} {e}^{−{x}^{\mathrm{3}} } \mathrm{ln}\left(\mathrm{1}+{x}\right){dx} \\ $$$${let}\:\int{dv}=\int{x}^{\mathrm{5}} {e}^{−{x}^{\mathrm{3}} } {dx}\:\:\:{put}\:{y}={x}^{\mathrm{3}} \\ $$$${V}=\frac{\mathrm{1}}{\mathrm{3}}\int{ye}^{−{y}} {dy}\:\:\:\:{by}\:{IBP} \\ $$$${V}=−\frac{\mathrm{1}}{\mathrm{3}}{ye}^{−{y}} +\int{e}^{−{y}} {dy}=−\frac{\mathrm{1}}{\mathrm{3}}{e}^{−{y}} \left({y}+\mathrm{1}\right)+{k}\:\:{but}\:{y}={x}^{\mathrm{3}} \\ $$$$\because{V}=−\frac{\mathrm{1}}{\mathrm{3}}{e}^{−{x}^{\mathrm{3}} } \left({x}^{\mathrm{3}} +\mathrm{1}\right)+{k}\:\:{and}\:{u}=\mathrm{ln}\left(\mathrm{1}+{x}\right),{du}=\frac{\mathrm{1}}{\mathrm{1}+{x}} \\ $$$${usingIBP}\:\:\:\:\:\:\int{udv}={uv}−\int{vdu} \\ $$$${I}=\mathrm{9}\left(−\frac{\mathrm{1}}{\mathrm{3}}{e}^{−{x}^{\mathrm{3}} } \left({x}^{\mathrm{3}} +\mathrm{1}\right)\mathrm{ln}\left(\mathrm{1}+{x}\right)\right)_{\mathrm{0}} ^{\infty} +\frac{\mathrm{9}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}+{x}^{\mathrm{3}} }{\mathrm{1}+{x}}\right){e}^{−{x}^{\mathrm{3}} } {dx} \\ $$$${I}=\mathrm{0}+\mathrm{3}\underset{\mathrm{0}} {\int}^{\infty} \left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right){e}^{−{x}^{\mathrm{3}} } {dx}\:\:\:{let} \\ $$$${y}={x}^{\mathrm{3}} ,{x}^{\frac{\mathrm{1}}{\mathrm{3}}} \:{and}\:{dx}=\frac{\mathrm{1}}{\mathrm{3}}{y}^{−\frac{\mathrm{2}}{\mathrm{3}}} {dy} \\ $$$${I}=\mathrm{3}\int_{\mathrm{0}} ^{\infty} \left({y}^{\frac{\mathrm{2}}{\mathrm{3}}} −{y}^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{1}\right){e}^{−{y}} ×\frac{\mathrm{1}}{\mathrm{3}}{y}^{−\frac{\mathrm{2}}{\mathrm{3}}} {dy} \\ $$$${I}=\int_{\mathrm{0}} ^{\infty} \left(\mathrm{1}−{y}^{−\frac{\mathrm{1}}{\mathrm{3}}} +{y}^{−\frac{\mathrm{2}}{\mathrm{3}}} \right){e}^{−{y}} {dy} \\ $$$${I}=\int_{\mathrm{0}} ^{\infty} {y}^{\mathrm{1}−\mathrm{1}} {e}^{−{y}} {dy}−\int_{\mathrm{0}} ^{\infty} {y}^{\frac{\mathrm{2}}{\mathrm{3}}−\mathrm{1}} {e}^{−{y}} {dy}+\int_{\mathrm{0}} ^{\infty} {y}^{\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}} {e}^{−{y}} {dy} \\ $$$${I}=\Gamma\left(\mathrm{1}\right)−\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right)+\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$\because\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{5}} {e}^{−{x}^{\mathrm{3}} } \mathrm{ln}\left(\mathrm{1}+{x}\right){dx}=\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)−\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right)+\Gamma\left(\frac{\mathrm{3}}{\mathrm{3}}\right)\:\:{Q}.{E}.{D} \\ $$$${by}\:{mathdave}\left(\mathrm{24}/\mathrm{09}/\mathrm{2020}\right) \\ $$$$\: \\ $$
Commented by mnjuly1970 last updated on 24/Sep/20

$${thank}\:{you} \\ $$
Commented by Tawa11 last updated on 06/Sep/21

$$\mathrm{great}\:\mathrm{sir} \\ $$
