Menu Close

Nice-Mathematics-calculation-0-1-tanh-1-x-x-dx-pi-2-4-x-t-2-0-1-tanh-1-t-t-

Tinku Tara 0 Comments
Pin




Question Number 157251 by mnjuly1970 last updated on 21/Oct/21
# Nice Mathematics # ...calculation ... Ω :=∫_0 ^( 1) (( tanh^( −1) ((√( x)) ))/x) dx =^? (( π^( 2) )/4) −−−−−−−−−−−−− Ω :=^((√x) = t) 2∫_0 ^( 1) (( tanh^( −1) (t ))/t) dt :=^({tanh^( −1) (t )= (1/2) ln( ((1+t)/(1−t)) ) }) ∫_0 ^( 1) ((ln( 1+t )− ln(1−t ))/t) dt : = −Li_( 2) (−1 ) + Li_( 2) (1 ) :=^( {Li_( 2) (z )= Σ_(n=1) ^∞ (( z^( n) )/n^( 2) ) }) η (2) + ζ (2) := (π^( 2) /(12)) + (π^( 2) /6) = (( π^( 2) )/( 4)) ■ m.n
$$ \\ $$$$\:\:\:\:\:#\:\mathrm{Nice}\:\mathrm{Mathematics}\:# \\ $$$$\:\:\:\:\:\:\:…{calculation}\:… \\ $$$$\:\:\:\:\:\:\:\:\Omega\::=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:{tanh}^{\:−\mathrm{1}} \:\left(\sqrt{\:{x}}\:\right)}{{x}}\:{dx}\:\overset{?} {=}\:\frac{\:\pi^{\:\mathrm{2}} }{\mathrm{4}} \\ $$$$\:\:\:−−−−−−−−−−−−− \\ $$$$\:\:\:\:\Omega\::\overset{\sqrt{{x}}\:=\:{t}} {=}\:\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:{tanh}^{\:−\mathrm{1}} \:\left({t}\:\right)}{{t}}\:{dt} \\ $$$$\:\:\:\:\:\:\:\:\::\overset{\left\{{tanh}^{\:−\mathrm{1}} \:\left({t}\:\right)=\:\frac{\mathrm{1}}{\mathrm{2}}\:{ln}\left(\:\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}\:\right)\:\right\}} {=}\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}\left(\:\mathrm{1}+{t}\:\right)−\:{ln}\left(\mathrm{1}−{t}\:\right)}{{t}}\:{dt} \\ $$$$\:\:\:\::\:\:=\:\:−\mathrm{Li}_{\:\mathrm{2}} \:\left(−\mathrm{1}\:\right)\:+\:\mathrm{Li}_{\:\mathrm{2}} \:\left(\mathrm{1}\:\right) \\ $$$$\:\:\:\:\::\overset{\:\left\{\mathrm{Li}_{\:\mathrm{2}} \:\left({z}\:\right)=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\:{z}^{\:{n}} }{{n}^{\:\mathrm{2}} }\:\right\}} {=}\:\:\eta\:\left(\mathrm{2}\right)\:+\:\zeta\:\left(\mathrm{2}\right)\: \\ $$$$\:\:\:\:\::=\:\:\frac{\pi^{\:\mathrm{2}} }{\mathrm{12}}\:+\:\frac{\pi^{\:\mathrm{2}} }{\mathrm{6}}\:\:=\:\frac{\:\pi^{\:\mathrm{2}} }{\:\mathrm{4}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\blacksquare\:{m}.{n}\:\:\:\:\:\: \\ $$$$ \\ $$
Answered by qaz last updated on 21/Oct/21
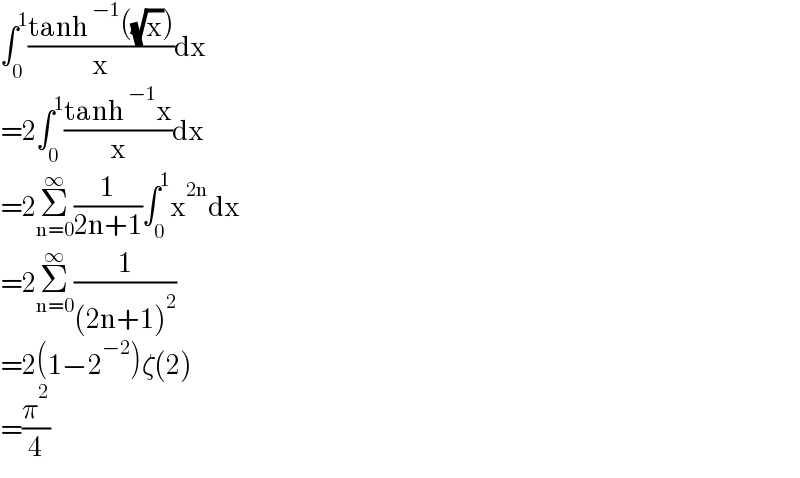
∫_0 ^1 ((tanh^(−1) ((√x)))/x)dx =2∫_0 ^1 ((tanh^(−1) x)/x)dx =2Σ_(n=0) ^∞ (1/(2n+1))∫_0 ^1 x^(2n) dx =2Σ_(n=0) ^∞ (1/((2n+1)^2 )) =2(1−2^(−2) )ζ(2) =(π^2 /4)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{tanh}\:^{−\mathrm{1}} \left(\sqrt{\mathrm{x}}\right)}{\mathrm{x}}\mathrm{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{tanh}\:^{−\mathrm{1}} \mathrm{x}}{\mathrm{x}}\mathrm{dx} \\ $$$$=\mathrm{2}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{2n}} \mathrm{dx} \\ $$$$=\mathrm{2}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{2}\left(\mathrm{1}−\mathrm{2}^{−\mathrm{2}} \right)\zeta\left(\mathrm{2}\right) \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$
Commented by mnjuly1970 last updated on 21/Oct/21
thanks alot sir qaz
$$\:{thanks}\:{alot}\:{sir}\:{qaz} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *