Question Number 123550 by mnjuly1970 last updated on 26/Nov/20
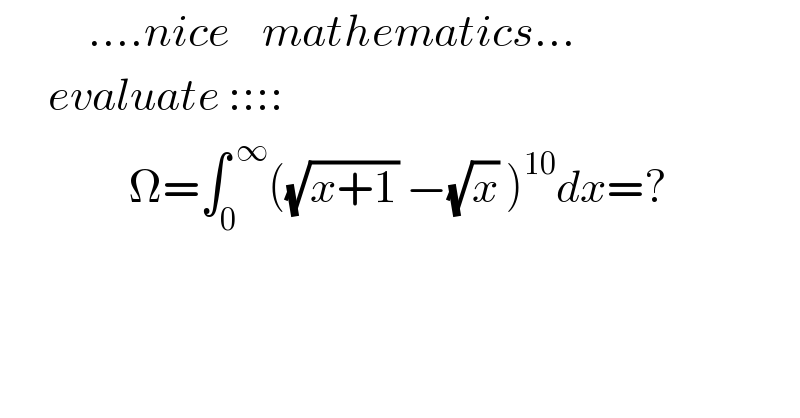
$$\:\:\:\:\:\:\:\:\:\:\:….{nice}\:\:\:\:{mathematics}… \\ $$$$\:\:\:\:\:\:{evaluate}\::::: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\infty} \left(\sqrt{{x}+\mathrm{1}}\:−\sqrt{{x}}\:\right)^{\mathrm{10}} {dx}=? \\ $$
Answered by Olaf last updated on 26/Nov/20
![Let x = sinh^2 u dx = 2sinhucoshudu = sinh(2u)du Ω = ∫_0 ^∞ ((√(1+sinh^2 u))−(√(sinh^2 u)))^(10) sinh(2u)du Ω = ∫_0 ^∞ (coshu−sinhu)^(10) sinh(2u)du Ω = ∫_0 ^∞ (e^(−u) )^(10) ((e^(2u) −e^(−2u) )/2)du Ω = ∫_0 ^∞ ((e^(−8u) −e^(−12u) )/2)du Ω = [((−(1/8)e^(−8u) +(1/(12))e^(−12u) )/2)]_0 ^∞ Ω = −(1/2)(−(1/8)+(1/(12))) Ω = (1/(48))](https://www.tinkutara.com/question/Q123554.png)
$$\mathrm{Let}\:{x}\:=\:\mathrm{sinh}^{\mathrm{2}} {u} \\ $$$${dx}\:=\:\mathrm{2sinh}{u}\mathrm{cosh}{udu}\:=\:\mathrm{sinh}\left(\mathrm{2}{u}\right){du} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\infty} \left(\sqrt{\mathrm{1}+\mathrm{sinh}^{\mathrm{2}} {u}}−\sqrt{\mathrm{sinh}^{\mathrm{2}} {u}}\right)^{\mathrm{10}} \mathrm{sinh}\left(\mathrm{2}{u}\right){du} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\infty} \left(\mathrm{cosh}{u}−\mathrm{sinh}{u}\right)^{\mathrm{10}} \mathrm{sinh}\left(\mathrm{2}{u}\right){du} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\infty} \left({e}^{−{u}} \right)^{\mathrm{10}} \frac{{e}^{\mathrm{2}{u}} −{e}^{−\mathrm{2}{u}} }{\mathrm{2}}{du} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−\mathrm{8}{u}} −{e}^{−\mathrm{12}{u}} }{\mathrm{2}}{du} \\ $$$$\Omega\:=\:\left[\frac{−\frac{\mathrm{1}}{\mathrm{8}}{e}^{−\mathrm{8}{u}} +\frac{\mathrm{1}}{\mathrm{12}}{e}^{−\mathrm{12}{u}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\infty} \\ $$$$\Omega\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{12}}\right) \\ $$$$\Omega\:=\:\frac{\mathrm{1}}{\mathrm{48}}\: \\ $$
Commented by mnjuly1970 last updated on 26/Nov/20
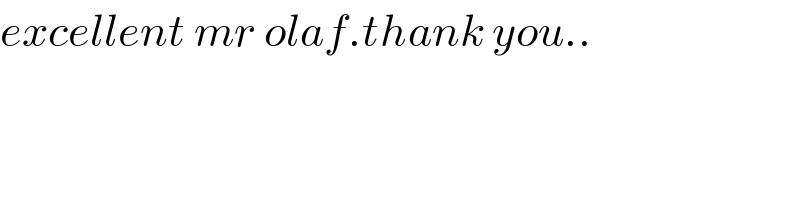
$${excellent}\:{mr}\:{olaf}.{thank}\:{you}.. \\ $$
Answered by MJS_new last updated on 26/Nov/20
![∫((√(x+1))−(√x))^(10) dx= [t=((√(x+1))−(√x))^(10) → dx=−(((√x)(√(x+1)))/(5((√(x+1))−(√x))^(10) ))dt] =(1/(20))∫((t^(2/5) −1)/t^(1/5) )dt=(t^(6/5) /(24))−(t^(4/5) /(16)) borders for x: [0; ∞) ⇒ borders for t: [1; 0] ⇒ answer is (1/(48))](https://www.tinkutara.com/question/Q123566.png)
$$\int\left(\sqrt{{x}+\mathrm{1}}−\sqrt{{x}}\right)^{\mathrm{10}} {dx}= \\ $$$$\:\:\:\:\:\left[{t}=\left(\sqrt{{x}+\mathrm{1}}−\sqrt{{x}}\right)^{\mathrm{10}} \:\rightarrow\:{dx}=−\frac{\sqrt{{x}}\sqrt{{x}+\mathrm{1}}}{\mathrm{5}\left(\sqrt{{x}+\mathrm{1}}−\sqrt{{x}}\right)^{\mathrm{10}} }{dt}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{20}}\int\frac{{t}^{\mathrm{2}/\mathrm{5}} −\mathrm{1}}{{t}^{\mathrm{1}/\mathrm{5}} }{dt}=\frac{{t}^{\mathrm{6}/\mathrm{5}} }{\mathrm{24}}−\frac{{t}^{\mathrm{4}/\mathrm{5}} }{\mathrm{16}} \\ $$$$\mathrm{borders}\:\mathrm{for}\:{x}:\:\left[\mathrm{0};\:\infty\right)\:\Rightarrow\:\mathrm{borders}\:\mathrm{for}\:{t}:\:\left[\mathrm{1};\:\mathrm{0}\right] \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{1}}{\mathrm{48}} \\ $$
Commented by MJS_new last updated on 26/Nov/20
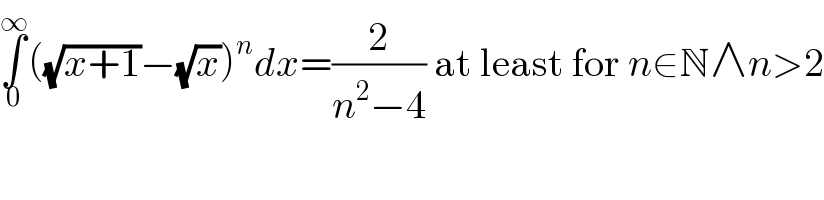
$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\left(\sqrt{{x}+\mathrm{1}}−\sqrt{{x}}\right)^{{n}} {dx}=\frac{\mathrm{2}}{{n}^{\mathrm{2}} −\mathrm{4}}\:\mathrm{at}\:\mathrm{least}\:\mathrm{for}\:{n}\in\mathbb{N}\wedge{n}>\mathrm{2} \\ $$
Commented by MJS_new last updated on 26/Nov/20
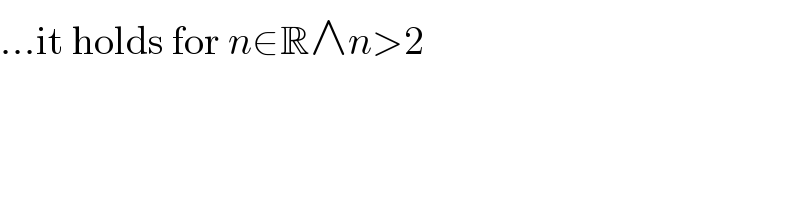
$$…\mathrm{it}\:\mathrm{holds}\:\mathrm{for}\:{n}\in\mathbb{R}\wedge{n}>\mathrm{2} \\ $$
Commented by mnjuly1970 last updated on 26/Nov/20
$${grateful}\:{mr}\:{MJS}..\: \\ $$
Commented by mnjuly1970 last updated on 26/Nov/20

$$ \\ $$
Answered by mathmax by abdo last updated on 26/Nov/20
![let I_n =∫_0 ^∞ ((√(x+1))−(√x))^n dx changement x=sh^2 t give I_n =∫_0 ^∞ (ch(t)−sh(t))^n 2sh(t)cht dt =∫_0 ^∞ (((e^t +e^(−t) )/2)−((e^t −e^(−t) )/2))^n sh(2t)dt =∫_0 ^∞ e^(−nt) ×((e^(2t) −e^(−2t) )/2) dt =(1/2)∫_0 ^∞ (e^(−(n−2)t) −e^(−(n+2)t) )dt =(1/2)[−(1/(n−2))e^(−(n−2)t) +(1/(n+2))e^(−(n+2)t) ]_0 ^∞ =(1/2){(1/(n−2))−(1/(n+2))}=(1/2)×((n+2−n+2)/(n^2 −4))=(2/(n^2 −4)) n=10 ⇒ ∫_0 ^∞ ((√(x+1))−(√x))^(10) dx =(2/(100−4))=(2/(96))=(1/(48))](https://www.tinkutara.com/question/Q123624.png)
$$\mathrm{let}\:\mathrm{I}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\infty} \left(\sqrt{\mathrm{x}+\mathrm{1}}−\sqrt{\mathrm{x}}\right)^{\mathrm{n}} \:\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{x}=\mathrm{sh}^{\mathrm{2}} \mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{I}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\infty} \:\:\left(\mathrm{ch}\left(\mathrm{t}\right)−\mathrm{sh}\left(\mathrm{t}\right)\right)^{\mathrm{n}} \mathrm{2sh}\left(\mathrm{t}\right)\mathrm{cht}\:\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{e}^{\mathrm{t}} \:+\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}−\frac{\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}\right)^{\mathrm{n}} \:\mathrm{sh}\left(\mathrm{2t}\right)\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{nt}} \:×\frac{\mathrm{e}^{\mathrm{2t}} −\mathrm{e}^{−\mathrm{2t}} }{\mathrm{2}}\:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\left(\mathrm{e}^{−\left(\mathrm{n}−\mathrm{2}\right)\mathrm{t}} −\mathrm{e}^{−\left(\mathrm{n}+\mathrm{2}\right)\mathrm{t}} \right)\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[−\frac{\mathrm{1}}{\mathrm{n}−\mathrm{2}}\mathrm{e}^{−\left(\mathrm{n}−\mathrm{2}\right)\mathrm{t}} +\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}\mathrm{e}^{−\left(\mathrm{n}+\mathrm{2}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{1}}{\mathrm{n}−\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}\right\}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{n}+\mathrm{2}−\mathrm{n}+\mathrm{2}}{\mathrm{n}^{\mathrm{2}} −\mathrm{4}}=\frac{\mathrm{2}}{\mathrm{n}^{\mathrm{2}} −\mathrm{4}} \\ $$$$\mathrm{n}=\mathrm{10}\:\Rightarrow\:\int_{\mathrm{0}} ^{\infty} \left(\sqrt{\mathrm{x}+\mathrm{1}}−\sqrt{\mathrm{x}}\right)^{\mathrm{10}} \mathrm{dx}\:=\frac{\mathrm{2}}{\mathrm{100}−\mathrm{4}}=\frac{\mathrm{2}}{\mathrm{96}}=\frac{\mathrm{1}}{\mathrm{48}} \\ $$
Commented by mnjuly1970 last updated on 27/Nov/20
$${thanks}\:{a}\:{lot}\:{sir}\:{max} \\ $$
