Question Number 114996 by mnjuly1970 last updated on 22/Sep/20
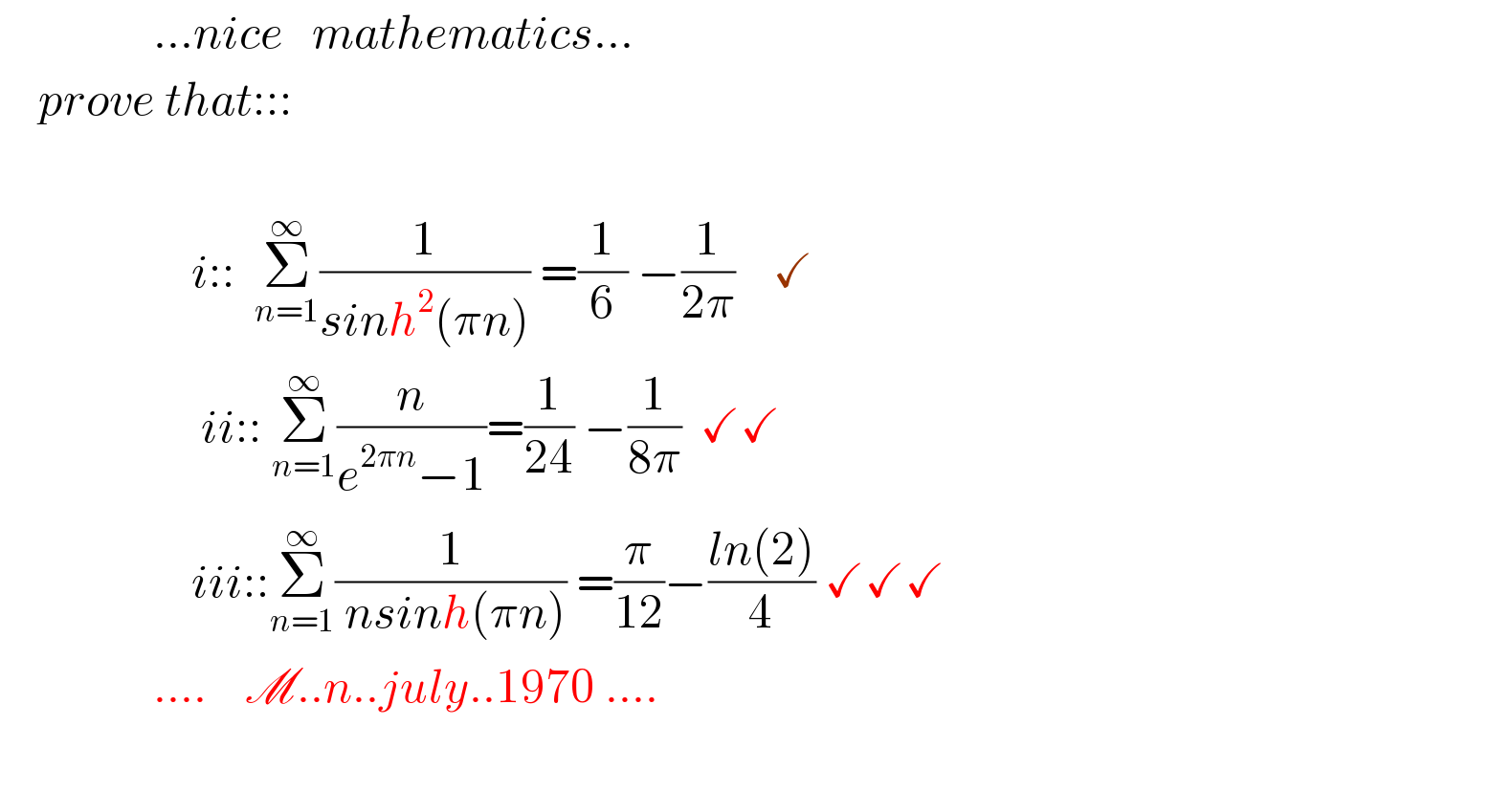
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…{nice}\:\:\:{mathematics}…\: \\ $$$$\:\:\:\:{prove}\:{that}::: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{i}::\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{sinh}^{\mathrm{2}} \left(\pi{n}\right)}\:=\frac{\mathrm{1}}{\mathrm{6}}\:−\frac{\mathrm{1}}{\mathrm{2}\pi}\:\:\:\:\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{ii}::\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}}{{e}^{\mathrm{2}\pi{n}} −\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{24}}\:−\frac{\mathrm{1}}{\mathrm{8}\pi}\:\:\checkmark\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{iii}::\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\:{nsinh}\left(\pi{n}\right)}\:=\frac{\pi}{\mathrm{12}}−\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{4}}\:\checkmark\checkmark\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….\:\:\:\:\mathscr{M}..{n}..{july}..\mathrm{1970}\:…. \\ $$$$ \\ $$
Commented by maths mind last updated on 24/Sep/20
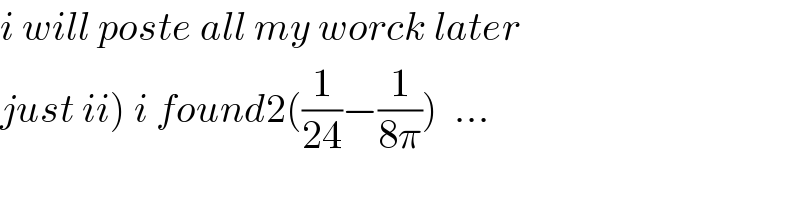
$${i}\:{will}\:{poste}\:{all}\:{my}\:{worck}\:{later}\: \\ $$$$\left.{just}\:{ii}\right)\:{i}\:{found}\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{24}}−\frac{\mathrm{1}}{\mathrm{8}\pi}\right)\:\:… \\ $$
Answered by Olaf last updated on 23/Sep/20
![i:: I_n = ∫_n ^(n+1) (dx/(sinh^2 (πx))) I_n = ∫_n ^(n+1) (coth^2 (πx)−1)dx I_n = [(−(1/π)coth(πx)]_n ^(n+1) = (1/π)[coth(πn)−coth(π(n+1))] I_n = (1/π)[((cosh(πn))/(sinh(πn)))−((cosh(π(n+1)))/(sinh(π(n+1))))] I_n =(1/π) ((sinh(π(n+1))cosh(πn)−cosh(π(n+1)+cosh(πn))/(sinh(πn)sinh(π(n+1)))) I_n = (1/π)[((sinh(π(n+1)−πn])/(sinh(πn)sinh(π(n+1))))] I_n = (1/π)[((sinh(π))/(sinh(πn)sinh(π(n+1))))] (π/(sinh(π)))I_n = (1/(sinh(πn)sinh(π(n+1)))) (π/(sinh(π)))I_(n+1) ≤ (1/(sinh^2 (π(n+1)))) ≤ (π/(sinh(π)))I_n (π/(sinh(π)))Σ_(n=1) ^∞ I_(n+1) ≤ Σ_(n=1) ^∞ (1/(sinh^2 (π(n+1)))) ≤Σ_(n=1) ^∞ (π/(sinh(π)))I_n (π/(sinh(π)))Σ_(n=2) ^∞ I_n ≤ Σ_(n=1) ^∞ (1/(sinh^2 (πn)))−(1/(sinh^2 (π))) ≤Σ_(n=1) ^∞ (π/(sinh(π)))I_n (π/(sinh(π)))[−(1/π)coth(πx)]_2 ^∞ ≤ Σ_(n=1) ^∞ (1/(sinh^2 (πn)))−(1/(sinh^2 (π))) ≤ (π/(sinh(π)))[−(1/π)coth(πx)]_1 ^∞ (1/(sinh(π)))[coth(2π)−1] ≤ Σ_(n=1) ^∞ (1/(sinh^2 (πn)))−(1/(sinh^2 (π))) ≤ (1/(sinh(π)))[coth(π)−1] (1/(sinh(π)))[coth(2π)−1+(1/(sinh(π)))] ≤ Σ_(n=1) ^∞ (1/(sinh^2 (πn))) ≤ (1/(sinh(π)))[coth(π)−1+(1/(sinh(π)))]_1 ^∞ ((coth(2π)sinh(π)−sinh(π)+1)/(sinh^2 (π))) ≤ Σ_(n=1) ^∞ (1/(sinh^2 (πn))) ≤ [((cosh(π)−sinh(π)+1)/(sinh^2 (π)))] I tried but may be it is not the good way.](https://www.tinkutara.com/question/Q115160.png)
$${i}:: \\ $$$$\mathrm{I}_{{n}} \:=\:\int_{{n}} ^{{n}+\mathrm{1}} \frac{{dx}}{\mathrm{sinh}^{\mathrm{2}} \left(\pi{x}\right)} \\ $$$$\mathrm{I}_{{n}} \:=\:\int_{{n}} ^{{n}+\mathrm{1}} \left(\mathrm{coth}^{\mathrm{2}} \left(\pi{x}\right)−\mathrm{1}\right){dx} \\ $$$$\mathrm{I}_{{n}} \:=\:\left[\left(−\frac{\mathrm{1}}{\pi}\mathrm{coth}\left(\pi{x}\right)\right]_{{n}} ^{{n}+\mathrm{1}} =\:\frac{\mathrm{1}}{\pi}\left[\mathrm{coth}\left(\pi{n}\right)−\mathrm{coth}\left(\pi\left({n}+\mathrm{1}\right)\right)\right]\right. \\ $$$$\mathrm{I}_{{n}} \:\:=\:\frac{\mathrm{1}}{\pi}\left[\frac{\mathrm{cosh}\left(\pi{n}\right)}{\mathrm{sinh}\left(\pi{n}\right)}−\frac{\mathrm{cosh}\left(\pi\left({n}+\mathrm{1}\right)\right)}{\mathrm{sinh}\left(\pi\left({n}+\mathrm{1}\right)\right)}\right] \\ $$$$\mathrm{I}_{{n}} \:\:=\frac{\mathrm{1}}{\pi}\:\frac{\mathrm{sinh}\left(\pi\left({n}+\mathrm{1}\right)\right)\mathrm{cosh}\left(\pi{n}\right)−\mathrm{cosh}\left(\pi\left({n}+\mathrm{1}\right)+\mathrm{cosh}\left(\pi{n}\right)\right.}{\mathrm{sinh}\left(\pi{n}\right)\mathrm{sinh}\left(\pi\left({n}+\mathrm{1}\right)\right)} \\ $$$$\mathrm{I}_{{n}} \:\:=\:\frac{\mathrm{1}}{\pi}\left[\frac{\mathrm{sinh}\left(\pi\left({n}+\mathrm{1}\right)−\pi{n}\right]}{\mathrm{sinh}\left(\pi{n}\right)\mathrm{sinh}\left(\pi\left({n}+\mathrm{1}\right)\right)}\right] \\ $$$$\mathrm{I}_{{n}} \:\:=\:\frac{\mathrm{1}}{\pi}\left[\frac{\mathrm{sinh}\left(\pi\right)}{\mathrm{sinh}\left(\pi{n}\right)\mathrm{sinh}\left(\pi\left({n}+\mathrm{1}\right)\right)}\right] \\ $$$$\frac{\pi}{\mathrm{sinh}\left(\pi\right)}\mathrm{I}_{{n}} \:=\:\frac{\mathrm{1}}{\mathrm{sinh}\left(\pi{n}\right)\mathrm{sinh}\left(\pi\left({n}+\mathrm{1}\right)\right)} \\ $$$$\frac{\pi}{\mathrm{sinh}\left(\pi\right)}\mathrm{I}_{{n}+\mathrm{1}} \:\leqslant\:\frac{\mathrm{1}}{\mathrm{sinh}^{\mathrm{2}} \left(\pi\left({n}+\mathrm{1}\right)\right)}\:\leqslant\:\frac{\pi}{\mathrm{sinh}\left(\pi\right)}\mathrm{I}_{{n}} \\ $$$$\frac{\pi}{\mathrm{sinh}\left(\pi\right)}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{I}_{{n}+\mathrm{1}} \:\leqslant\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{sinh}^{\mathrm{2}} \left(\pi\left({n}+\mathrm{1}\right)\right)}\:\leqslant\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\pi}{\mathrm{sinh}\left(\pi\right)}\mathrm{I}_{{n}} \\ $$$$\frac{\pi}{\mathrm{sinh}\left(\pi\right)}\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\mathrm{I}_{{n}} \:\leqslant\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{sinh}^{\mathrm{2}} \left(\pi{n}\right)}−\frac{\mathrm{1}}{\mathrm{sinh}^{\mathrm{2}} \left(\pi\right)}\:\leqslant\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\pi}{\mathrm{sinh}\left(\pi\right)}\mathrm{I}_{{n}} \\ $$$$\frac{\pi}{\mathrm{sinh}\left(\pi\right)}\left[−\frac{\mathrm{1}}{\pi}\mathrm{coth}\left(\pi{x}\right)\right]_{\mathrm{2}} ^{\infty} \:\leqslant\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{sinh}^{\mathrm{2}} \left(\pi{n}\right)}−\frac{\mathrm{1}}{\mathrm{sinh}^{\mathrm{2}} \left(\pi\right)}\:\leqslant\:\frac{\pi}{\mathrm{sinh}\left(\pi\right)}\left[−\frac{\mathrm{1}}{\pi}\mathrm{coth}\left(\pi{x}\right)\right]_{\mathrm{1}} ^{\infty} \\ $$$$\frac{\mathrm{1}}{\mathrm{sinh}\left(\pi\right)}\left[\mathrm{coth}\left(\mathrm{2}\pi\right)−\mathrm{1}\right]\:\leqslant\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{sinh}^{\mathrm{2}} \left(\pi{n}\right)}−\frac{\mathrm{1}}{\mathrm{sinh}^{\mathrm{2}} \left(\pi\right)}\:\leqslant\:\frac{\mathrm{1}}{\mathrm{sinh}\left(\pi\right)}\left[\mathrm{coth}\left(\pi\right)−\mathrm{1}\right] \\ $$$$\frac{\mathrm{1}}{\mathrm{sinh}\left(\pi\right)}\left[\mathrm{coth}\left(\mathrm{2}\pi\right)−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{sinh}\left(\pi\right)}\right]\:\leqslant\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{sinh}^{\mathrm{2}} \left(\pi{n}\right)}\:\leqslant\:\frac{\mathrm{1}}{\mathrm{sinh}\left(\pi\right)}\left[\mathrm{coth}\left(\pi\right)−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{sinh}\left(\pi\right)}\right]_{\mathrm{1}} ^{\infty} \\ $$$$\frac{\mathrm{coth}\left(\mathrm{2}\pi\right)\mathrm{sinh}\left(\pi\right)−\mathrm{sinh}\left(\pi\right)+\mathrm{1}}{\mathrm{sinh}^{\mathrm{2}} \left(\pi\right)}\:\:\leqslant\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{sinh}^{\mathrm{2}} \left(\pi{n}\right)}\:\leqslant\:\left[\frac{\mathrm{cosh}\left(\pi\right)−\mathrm{sinh}\left(\pi\right)+\mathrm{1}}{\mathrm{sinh}^{\mathrm{2}} \left(\pi\right)}\right] \\ $$$$\mathrm{I}\:\mathrm{tried}\:\mathrm{but}\:\mathrm{may}\:\mathrm{be}\:\mathrm{it}\:\mathrm{is}\:\mathrm{not}\:\mathrm{the}\:\mathrm{good}\:\mathrm{way}. \\ $$
Answered by maths mind last updated on 24/Sep/20

$$\left.{ii}\right) \\ $$$$\Sigma\frac{{n}}{{e}^{\mathrm{2}\pi{n}} −\mathrm{1}} \\ $$$${let}\:{f}\left({z}\right)=\frac{{z}}{{e}^{\mathrm{2}\pi{z}} −\mathrm{1}}\:\:\:\:{holomorphic}\:{cunction}\:{over}\:{C}−\left\{{iZ}\right\} \\ $$$${it}\:{has}\:{rvable}\:{singularity}\:{at}\:{origine} \\ $$$$\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{{z}}{{e}^{\mathrm{2}\pi{z}} −\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}\pi} \\ $$$${we}\:{can}\:{use} \\ $$$$\underset{{n}\geqslant\mathrm{0}} {\sum}{f}\left({n}\right)=\frac{\mathrm{1}}{\mathrm{2}\pi}+\underset{{n}\geqslant\mathrm{1}} {\sum}{f}\left({n}\right) \\ $$$$\underset{{n}\geqslant\mathrm{0}} {\sum}{f}\left({n}\right)=\int_{\mathrm{0}} ^{\infty} {f}\left({x}\right){dx}+\frac{{f}\left(\mathrm{0}\right)}{\mathrm{2}}+{i}\int_{\mathrm{0}} ^{\infty} \frac{{f}\left({it}\right)−{f}\left(−{it}\right)}{{e}^{\mathrm{2}\pi{t}} −\mathrm{1}}{dt}\:{Abel}\:−{plana}\:{formula} \\ $$$${f}\left({it}\right)−{f}\left(−{it}\right) \\ $$$$=\frac{{it}}{{e}^{\mathrm{2}{i}\pi{t}} −\mathrm{1}}+\frac{{it}}{{e}^{−\mathrm{2}{i}\pi{t}} −\mathrm{1}}\:=−{it}\Rightarrow{i}\int_{\mathrm{0}} ^{\infty} \frac{{f}\left({it}\right)−{f}\left(−{it}\right)}{{e}^{\mathrm{2}\pi{t}} −\mathrm{1}}{dt}=\int_{\mathrm{0}} ^{\infty} \frac{{x}}{{e}^{\mathrm{2}\pi{x}} −\mathrm{1}}{dx} \\ $$$$\underset{{n}\geqslant\mathrm{0}} {\sum}{f}\left({n}\underset{={S}} {\right)}=\frac{\mathrm{1}}{\mathrm{2}\pi}+\underset{{n}\geqslant\mathrm{1}} {\sum}{f}\left({n}\right)=\frac{\mathrm{1}}{\mathrm{2}\pi}+\underset{{n}\geqslant\mathrm{1}} {\sum}{f}\left({n}\right)=\frac{\mathrm{1}}{\mathrm{4}\pi}+\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{{xdx}}{{e}^{\mathrm{2}\pi{x}} −\mathrm{1}} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{{xdx}}{{e}^{\mathrm{2}\pi{x}} −\mathrm{1}},\mathrm{2}\pi{x}={t}\Rightarrow{dx}=\frac{{dt}}{\mathrm{2}\pi}\Rightarrow \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{4}\pi}−\frac{\mathrm{1}}{\mathrm{2}\pi}+\frac{\mathrm{1}}{\mathrm{2}\pi^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \frac{{t}}{{e}^{{t}} −\mathrm{1}}{dt}=−\frac{\mathrm{1}}{\mathrm{4}\pi}+\frac{\mathrm{1}}{\mathrm{2}\pi^{\mathrm{2}} }\zeta\left(\mathrm{2}\right)\Gamma\left(\mathrm{2}\right)=−\frac{\mathrm{1}}{\mathrm{4}\pi}+\frac{\mathrm{1}}{\mathrm{12}}. \\ $$$$\Sigma\frac{{n}}{{e}^{\mathrm{2}\pi{n}} −\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{12}}−\frac{\mathrm{1}}{\mathrm{4}\pi} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
