Menu Close

nice-mathematics-S-n-1-2n-n-16-n-

Tinku Tara 0 Comments
Pin




Question Number 151951 by mnjuly1970 last updated on 24/Aug/21
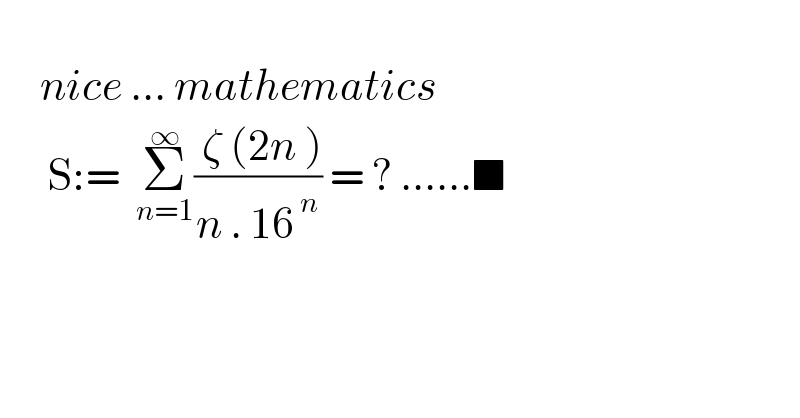
nice ... mathematics S:= Σ_(n=1) ^∞ (( ζ (2n ))/(n . 16^( n) )) = ? ......■
$$ \\ $$$$\:\:\:\:\:{nice}\:…\:{mathematics} \\ $$$$\:\:\:\:\:\:\mathrm{S}:=\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\:\zeta\:\left(\mathrm{2}{n}\:\right)}{{n}\:.\:\mathrm{16}^{\:{n}} }\:=\:?\:……\blacksquare \\ $$$$ \\ $$
Commented by Tawa11 last updated on 24/Aug/21
great
$$\mathrm{great} \\ $$
Answered by qaz last updated on 24/Aug/21
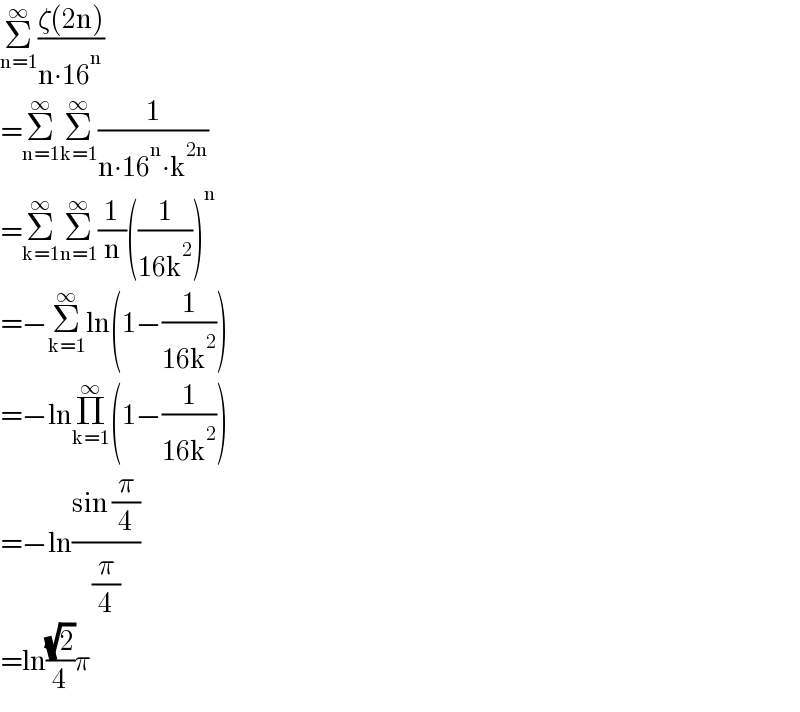
Σ_(n=1) ^∞ ((ζ(2n))/(n∙16^n )) =Σ_(n=1) ^∞ Σ_(k=1) ^∞ (1/(n∙16^n ∙k^(2n) )) =Σ_(k=1) ^∞ Σ_(n=1) ^∞ (1/n)((1/(16k^2 )))^n =−Σ_(k=1) ^∞ ln(1−(1/(16k^2 ))) =−lnΠ_(k=1) ^∞ (1−(1/(16k^2 ))) =−ln((sin (π/4))/(π/4)) =ln((√2)/4)π
$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\zeta\left(\mathrm{2n}\right)}{\mathrm{n}\centerdot\mathrm{16}^{\mathrm{n}} } \\ $$$$=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}\centerdot\mathrm{16}^{\mathrm{n}} \centerdot\mathrm{k}^{\mathrm{2n}} } \\ $$$$=\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}}\left(\frac{\mathrm{1}}{\mathrm{16k}^{\mathrm{2}} }\right)^{\mathrm{n}} \\ $$$$=−\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{16k}^{\mathrm{2}} }\right) \\ $$$$=−\mathrm{ln}\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{16k}^{\mathrm{2}} }\right) \\ $$$$=−\mathrm{ln}\frac{\mathrm{sin}\:\frac{\pi}{\mathrm{4}}}{\frac{\pi}{\mathrm{4}}} \\ $$$$=\mathrm{ln}\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\pi \\ $$
Commented by mnjuly1970 last updated on 24/Aug/21
thx alot master qaz...
$${thx}\:{alot}\:{master}\:{qaz}… \\ $$
Answered by Olaf_Thorendsen last updated on 24/Aug/21
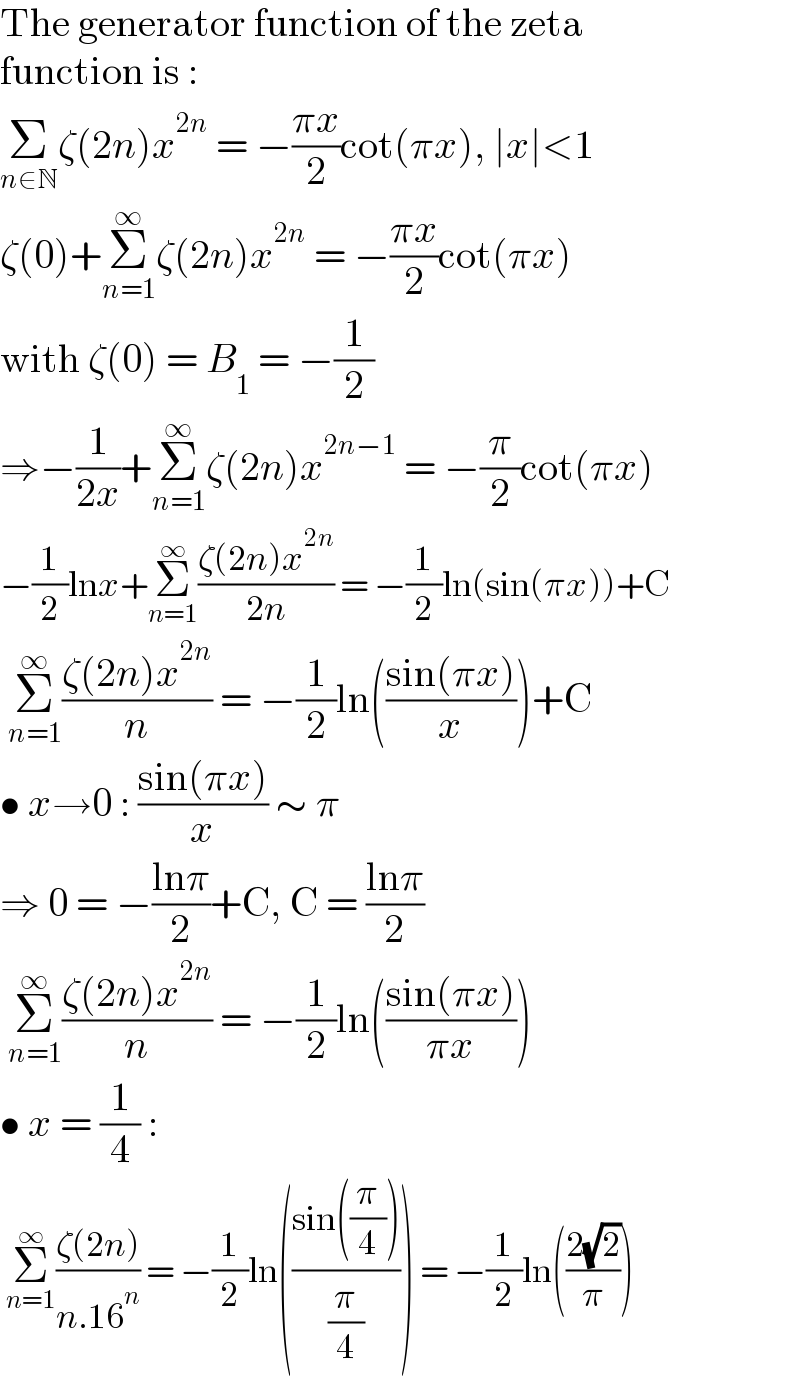
The generator function of the zeta function is : Σ_(n∈N) ζ(2n)x^(2n) = −((πx)/2)cot(πx), ∣x∣<1 ζ(0)+Σ_(n=1) ^∞ ζ(2n)x^(2n) = −((πx)/2)cot(πx) with ζ(0) = B_1 = −(1/2) ⇒−(1/(2x))+Σ_(n=1) ^∞ ζ(2n)x^(2n−1) = −(π/2)cot(πx) −(1/2)lnx+Σ_(n=1) ^∞ ((ζ(2n)x^(2n) )/(2n)) = −(1/2)ln(sin(πx))+C Σ_(n=1) ^∞ ((ζ(2n)x^(2n) )/n) = −(1/2)ln(((sin(πx))/x))+C • x→0 : ((sin(πx))/x) ∼ π ⇒ 0 = −((lnπ)/2)+C, C = ((lnπ)/2) Σ_(n=1) ^∞ ((ζ(2n)x^(2n) )/n) = −(1/2)ln(((sin(πx))/(πx))) • x = (1/4) : Σ_(n=1) ^∞ ((ζ(2n))/(n.16^n )) = −(1/2)ln(((sin((π/4)))/(π/4))) = −(1/2)ln(((2(√2))/π))
$$\mathrm{The}\:\mathrm{generator}\:\mathrm{function}\:\mathrm{of}\:\mathrm{the}\:\mathrm{zeta} \\ $$$$\mathrm{function}\:\mathrm{is}\:: \\ $$$$\underset{{n}\in\mathbb{N}} {\sum}\zeta\left(\mathrm{2}{n}\right){x}^{\mathrm{2}{n}} \:=\:−\frac{\pi{x}}{\mathrm{2}}\mathrm{cot}\left(\pi{x}\right),\:\mid{x}\mid<\mathrm{1} \\ $$$$\zeta\left(\mathrm{0}\right)+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\zeta\left(\mathrm{2}{n}\right){x}^{\mathrm{2}{n}} \:=\:−\frac{\pi{x}}{\mathrm{2}}\mathrm{cot}\left(\pi{x}\right) \\ $$$$\mathrm{with}\:\zeta\left(\mathrm{0}\right)\:=\:{B}_{\mathrm{1}} \:=\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow−\frac{\mathrm{1}}{\mathrm{2}{x}}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\zeta\left(\mathrm{2}{n}\right){x}^{\mathrm{2}{n}−\mathrm{1}} \:=\:−\frac{\pi}{\mathrm{2}}\mathrm{cot}\left(\pi{x}\right) \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}{x}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\zeta\left(\mathrm{2}{n}\right){x}^{\mathrm{2}{n}} }{\mathrm{2}{n}}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{sin}\left(\pi{x}\right)\right)+\mathrm{C} \\ $$$$\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\zeta\left(\mathrm{2}{n}\right){x}^{\mathrm{2}{n}} }{{n}}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{sin}\left(\pi{x}\right)}{{x}}\right)+\mathrm{C} \\ $$$$\bullet\:{x}\rightarrow\mathrm{0}\::\:\frac{\mathrm{sin}\left(\pi{x}\right)}{{x}}\:\sim\:\pi \\ $$$$\Rightarrow\:\mathrm{0}\:=\:−\frac{\mathrm{ln}\pi}{\mathrm{2}}+\mathrm{C},\:\mathrm{C}\:=\:\frac{\mathrm{ln}\pi}{\mathrm{2}} \\ $$$$\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\zeta\left(\mathrm{2}{n}\right){x}^{\mathrm{2}{n}} }{{n}}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{sin}\left(\pi{x}\right)}{\pi{x}}\right) \\ $$$$\bullet\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:: \\ $$$$\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\zeta\left(\mathrm{2}{n}\right)}{{n}.\mathrm{16}^{{n}} }\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}\right)}{\frac{\pi}{\mathrm{4}}}\right)\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\pi}\right) \\ $$
Commented by mnjuly1970 last updated on 24/Aug/21
thank you so much sir olaf..
$${thank}\:{you}\:{so}\:{much}\:{sir}\:{olaf}.. \\ $$
Answered by mnjuly1970 last updated on 24/Aug/21
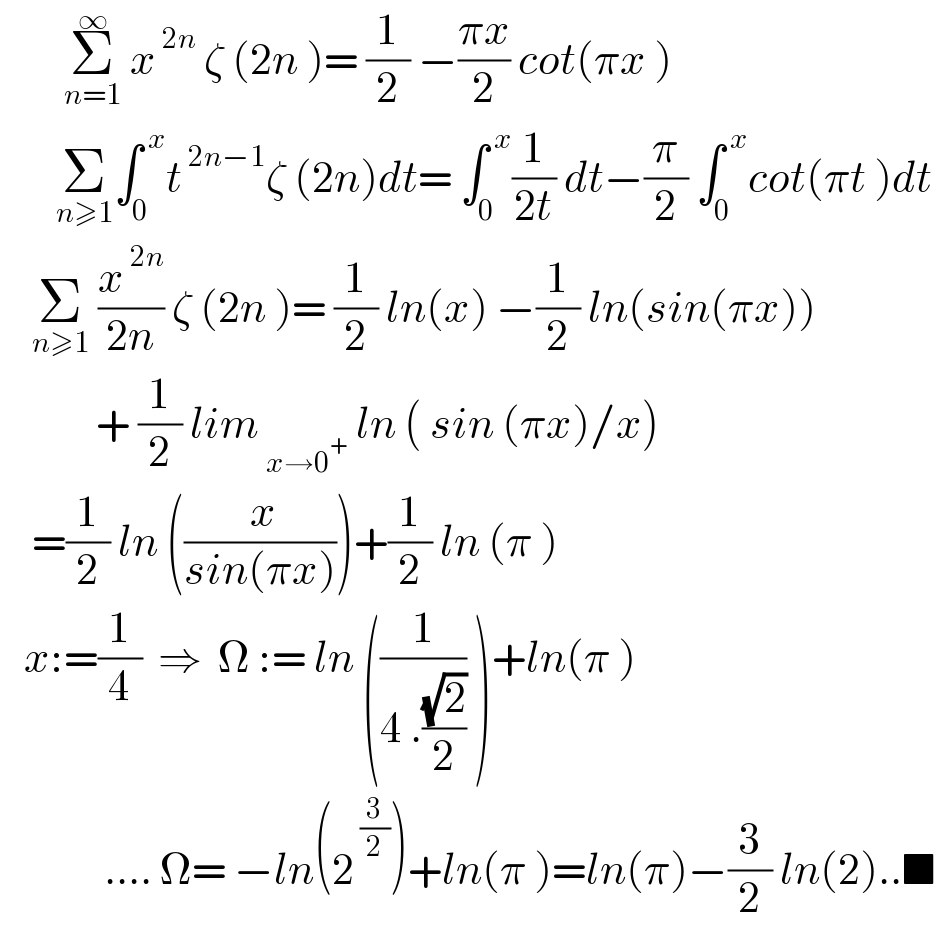
Σ_(n=1) ^∞ x^( 2n) ζ (2n )= (1/2) −((πx)/2) cot(πx ) Σ_(n≥1) ∫_0 ^( x) t^( 2n−1) ζ (2n)dt= ∫_0 ^( x) (1/(2t)) dt−(π/2) ∫_0 ^( x) cot(πt )dt Σ_(n≥1) (x^( 2n) /(2n)) ζ (2n )= (1/2) ln(x) −(1/2) ln(sin(πx)) + (1/2) lim_( x→0^+ ) ln ( sin (πx)/x) =(1/2) ln ((( x)/(sin(πx))))+(1/2) ln (π ) x:=(1/4) ⇒ Ω := ln ((1/(4 .((√2)/2))) )+ln(π ) .... Ω= −ln(2^( (3/2)) )+ln(π )=ln(π)−(3/2) ln(2)..■
$$\:\:\:\:\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:{x}^{\:\mathrm{2}{n}} \:\zeta\:\left(\mathrm{2}{n}\:\right)=\:\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\pi{x}}{\mathrm{2}}\:{cot}\left(\pi{x}\:\right) \\ $$$$\:\:\:\:\:\:\:\underset{{n}\geqslant\mathrm{1}} {\sum}\int_{\mathrm{0}} ^{\:{x}} {t}^{\:\mathrm{2}{n}−\mathrm{1}} \zeta\:\left(\mathrm{2}{n}\right){dt}=\:\int_{\mathrm{0}} ^{\:{x}} \frac{\mathrm{1}}{\mathrm{2}{t}}\:{dt}−\frac{\pi}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\:{x}} {cot}\left(\pi{t}\:\right){dt} \\ $$$$\:\:\:\:\underset{{n}\geqslant\mathrm{1}} {\sum}\:\frac{{x}^{\:\mathrm{2}{n}} }{\mathrm{2}{n}}\:\zeta\:\left(\mathrm{2}{n}\:\right)=\:\frac{\mathrm{1}}{\mathrm{2}}\:{ln}\left({x}\right)\:−\frac{\mathrm{1}}{\mathrm{2}}\:{ln}\left({sin}\left(\pi{x}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:+\:\frac{\mathrm{1}}{\mathrm{2}}\:{lim}_{\:{x}\rightarrow\mathrm{0}^{+} } \:{ln}\:\left(\:{sin}\:\left(\pi{x}\right)/{x}\right) \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\:{ln}\:\left(\frac{\:{x}}{{sin}\left(\pi{x}\right)}\right)+\frac{\mathrm{1}}{\mathrm{2}}\:{ln}\:\left(\pi\:\right) \\ $$$$\:\:\:{x}:=\frac{\mathrm{1}}{\mathrm{4}}\:\:\Rightarrow\:\:\Omega\::=\:{ln}\:\left(\frac{\mathrm{1}}{\mathrm{4}\:.\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\:\right)+{ln}\left(\pi\:\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:….\:\Omega=\:−{ln}\left(\mathrm{2}^{\:\frac{\mathrm{3}}{\mathrm{2}}} \right)+{ln}\left(\pi\:\right)={ln}\left(\pi\right)−\frac{\mathrm{3}}{\mathrm{2}}\:{ln}\left(\mathrm{2}\right)..\blacksquare \\ $$
Answered by mindispower last updated on 24/Aug/21
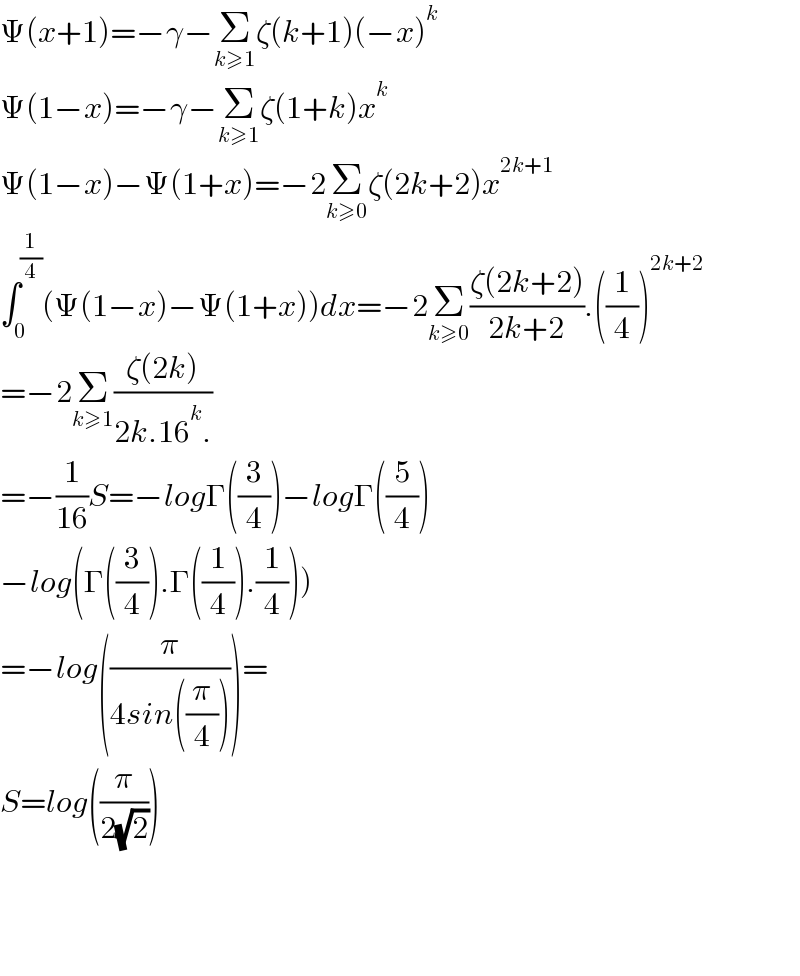
Ψ(x+1)=−γ−Σ_(k≥1) ζ(k+1)(−x)^k Ψ(1−x)=−γ−Σ_(k≥1) ζ(1+k)x^k Ψ(1−x)−Ψ(1+x)=−2Σ_(k≥0) ζ(2k+2)x^(2k+1) ∫_0 ^(1/4) (Ψ(1−x)−Ψ(1+x))dx=−2Σ_(k≥0) ((ζ(2k+2))/(2k+2)).((1/4))^(2k+2) =−2Σ_(k≥1) ((ζ(2k))/(2k.16^k .)) =−(1/(16))S=−logΓ((3/4))−logΓ((5/4)) −log(Γ((3/4)).Γ((1/4)).(1/4))) =−log((π/(4sin((π/4)))))= S=log((π/(2(√2))))
$$\Psi\left({x}+\mathrm{1}\right)=−\gamma−\underset{{k}\geqslant\mathrm{1}} {\sum}\zeta\left({k}+\mathrm{1}\right)\left(−{x}\right)^{{k}} \\ $$$$\Psi\left(\mathrm{1}−{x}\right)=−\gamma−\underset{{k}\geqslant\mathrm{1}} {\sum}\zeta\left(\mathrm{1}+{k}\right){x}^{{k}} \\ $$$$\Psi\left(\mathrm{1}−{x}\right)−\Psi\left(\mathrm{1}+{x}\right)=−\mathrm{2}\underset{{k}\geqslant\mathrm{0}} {\sum}\zeta\left(\mathrm{2}{k}+\mathrm{2}\right){x}^{\mathrm{2}{k}+\mathrm{1}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{4}}} \left(\Psi\left(\mathrm{1}−{x}\right)−\Psi\left(\mathrm{1}+{x}\right)\right){dx}=−\mathrm{2}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\zeta\left(\mathrm{2}{k}+\mathrm{2}\right)}{\mathrm{2}{k}+\mathrm{2}}.\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}{k}+\mathrm{2}} \\ $$$$=−\mathrm{2}\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\zeta\left(\mathrm{2}{k}\right)}{\mathrm{2}{k}.\mathrm{16}^{{k}} .} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{16}}{S}=−{log}\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)−{log}\Gamma\left(\frac{\mathrm{5}}{\mathrm{4}}\right) \\ $$$$\left.−{log}\left(\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right).\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right).\frac{\mathrm{1}}{\mathrm{4}}\right)\right) \\ $$$$=−{log}\left(\frac{\pi}{\mathrm{4}{sin}\left(\frac{\pi}{\mathrm{4}}\right)}\right)= \\ $$$${S}={log}\left(\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 24/Aug/21
sir power , thanks alot...
$${sir}\:{power}\:,\:{thanks}\:{alot}… \\ $$
Commented by mindispower last updated on 28/Aug/21
pleasur sir
$${pleasur}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *