Question Number 118546 by putriamalia last updated on 18/Oct/20
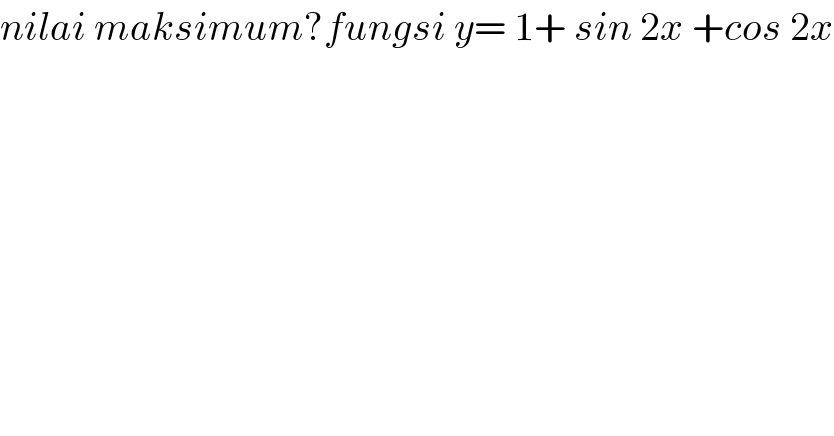
$${nilai}\:{maksimum}?{fungsi}\:{y}=\:\mathrm{1}+\:{sin}\:\mathrm{2}{x}\:+{cos}\:\mathrm{2}{x} \\ $$
Commented by mr W last updated on 18/Oct/20
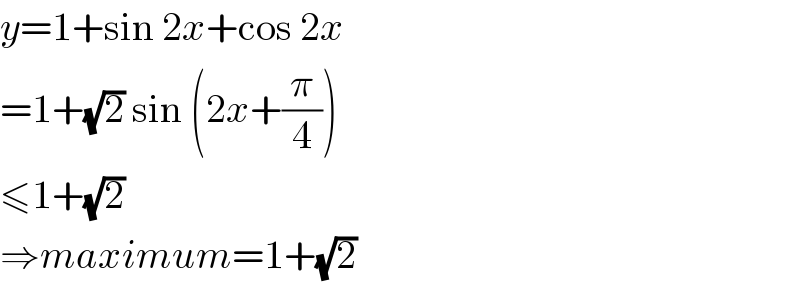
$${y}=\mathrm{1}+\mathrm{sin}\:\mathrm{2}{x}+\mathrm{cos}\:\mathrm{2}{x} \\ $$$$=\mathrm{1}+\sqrt{\mathrm{2}}\:\mathrm{sin}\:\left(\mathrm{2}{x}+\frac{\pi}{\mathrm{4}}\right) \\ $$$$\leqslant\mathrm{1}+\sqrt{\mathrm{2}} \\ $$$$\Rightarrow{maximum}=\mathrm{1}+\sqrt{\mathrm{2}} \\ $$
Commented by benjo_mathlover last updated on 18/Oct/20
$${hello}\:{mr}\:{W},\:{how}\:{are}\:{you}\:{sir}\:? \\ $$
Commented by mr W last updated on 18/Oct/20
$${things}\:{are}\:{ok}.\:{thanks}\:{sir}! \\ $$
Commented by benjo_mathlover last updated on 18/Oct/20
$${do}\:{you}\:{remember}\:{me}? \\ $$
Commented by benjo_mathlover last updated on 18/Oct/20
I am a long time member of this forum, but have been inactive for a while. I forgot my old account password. we've argued about math problems. haha .. at that time sir said my results were just a coincidence
Commented by mr W last updated on 18/Oct/20

$${i}\:{remember}\:{ID}\:{containing}\:{benjo}. \\ $$$${which}\:{ID}\:{were}\:{you}\:{using}? \\ $$
Commented by benjo_mathlover last updated on 18/Oct/20

$${yes}.\:{you}\:{are}\:{right}\: \\ $$
Answered by TANMAY PANACEA last updated on 18/Oct/20
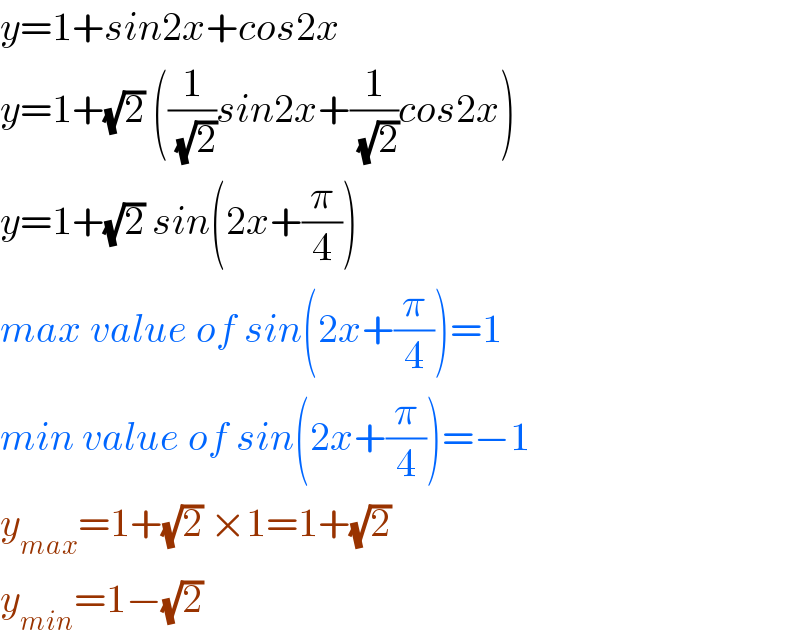
$${y}=\mathrm{1}+{sin}\mathrm{2}{x}+{cos}\mathrm{2}{x} \\ $$$${y}=\mathrm{1}+\sqrt{\mathrm{2}}\:\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{sin}\mathrm{2}{x}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{cos}\mathrm{2}{x}\right) \\ $$$${y}=\mathrm{1}+\sqrt{\mathrm{2}}\:{sin}\left(\mathrm{2}{x}+\frac{\pi}{\mathrm{4}}\right) \\ $$$${max}\:{value}\:{of}\:{sin}\left(\mathrm{2}{x}+\frac{\pi}{\mathrm{4}}\right)=\mathrm{1} \\ $$$${min}\:{value}\:{of}\:{sin}\left(\mathrm{2}{x}+\frac{\pi}{\mathrm{4}}\right)=−\mathrm{1} \\ $$$${y}_{{max}} =\mathrm{1}+\sqrt{\mathrm{2}}\:×\mathrm{1}=\mathrm{1}+\sqrt{\mathrm{2}}\: \\ $$$${y}_{{min}} =\mathrm{1}−\sqrt{\mathrm{2}}\: \\ $$
Answered by mathmax by abdo last updated on 18/Oct/20
![y(x)=1+sin(2x)+cos(2x) ⇒y(x)=1+(√2)cos(2x−(π/4)) ⇒ y^′ (x)=−2(√2)sin(2x−(π/4)) y^′ (x)=0 ⇒2x−(π/4)=kπ ⇒2x=kπ+(π/4) ⇒x=(π/8)+k(π/2) the period of y is π so we search the solution on[0,π] 0≤(π/4)+((kπ)/2)≤π ⇒o≤(1/4)+(k/2)≤1 ⇒−(1/4)≤(k/2)≤(3/4) ⇒ −(1/2)≤k≤(3/2) ⇒k=0 or1 ⇒x=(π/8) or x=((5π)/8) y((π/8))=1+(√2)cos(0) =1+(√2) after dressing the variation we get max f(x) =1+(√2)](https://www.tinkutara.com/question/Q118554.png)
$$\mathrm{y}\left(\mathrm{x}\right)=\mathrm{1}+\mathrm{sin}\left(\mathrm{2x}\right)+\mathrm{cos}\left(\mathrm{2x}\right)\:\Rightarrow\mathrm{y}\left(\mathrm{x}\right)=\mathrm{1}+\sqrt{\mathrm{2}}\mathrm{cos}\left(\mathrm{2x}−\frac{\pi}{\mathrm{4}}\right)\:\Rightarrow \\ $$$$\mathrm{y}^{'} \left(\mathrm{x}\right)=−\mathrm{2}\sqrt{\mathrm{2}}\mathrm{sin}\left(\mathrm{2x}−\frac{\pi}{\mathrm{4}}\right)\:\: \\ $$$$\mathrm{y}^{'} \left(\mathrm{x}\right)=\mathrm{0}\:\Rightarrow\mathrm{2x}−\frac{\pi}{\mathrm{4}}=\mathrm{k}\pi\:\Rightarrow\mathrm{2x}=\mathrm{k}\pi+\frac{\pi}{\mathrm{4}}\:\Rightarrow\mathrm{x}=\frac{\pi}{\mathrm{8}}+\mathrm{k}\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{the}\:\mathrm{period}\:\mathrm{of}\:\mathrm{y}\:\mathrm{is}\:\pi\:\:\:\:\mathrm{so}\:\:\:\:\mathrm{we}\:\mathrm{search}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{on}\left[\mathrm{0},\pi\right] \\ $$$$\mathrm{0}\leqslant\frac{\pi}{\mathrm{4}}+\frac{\mathrm{k}\pi}{\mathrm{2}}\leqslant\pi\:\Rightarrow\mathrm{o}\leqslant\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{k}}{\mathrm{2}}\leqslant\mathrm{1}\:\Rightarrow−\frac{\mathrm{1}}{\mathrm{4}}\leqslant\frac{\mathrm{k}}{\mathrm{2}}\leqslant\frac{\mathrm{3}}{\mathrm{4}}\:\Rightarrow \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\leqslant\mathrm{k}\leqslant\frac{\mathrm{3}}{\mathrm{2}}\:\Rightarrow\mathrm{k}=\mathrm{0}\:\mathrm{or1}\:\Rightarrow\mathrm{x}=\frac{\pi}{\mathrm{8}}\:\mathrm{or}\:\mathrm{x}=\frac{\mathrm{5}\pi}{\mathrm{8}} \\ $$$$\mathrm{y}\left(\frac{\pi}{\mathrm{8}}\right)=\mathrm{1}+\sqrt{\mathrm{2}}\mathrm{cos}\left(\mathrm{0}\right)\:=\mathrm{1}+\sqrt{\mathrm{2}}\:\:\mathrm{after}\:\mathrm{dressing}\:\mathrm{the}\:\mathrm{variation}\:\mathrm{we} \\ $$$$\mathrm{get}\:\mathrm{max}\:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{1}+\sqrt{\mathrm{2}} \\ $$
Answered by 1549442205PVT last updated on 18/Oct/20
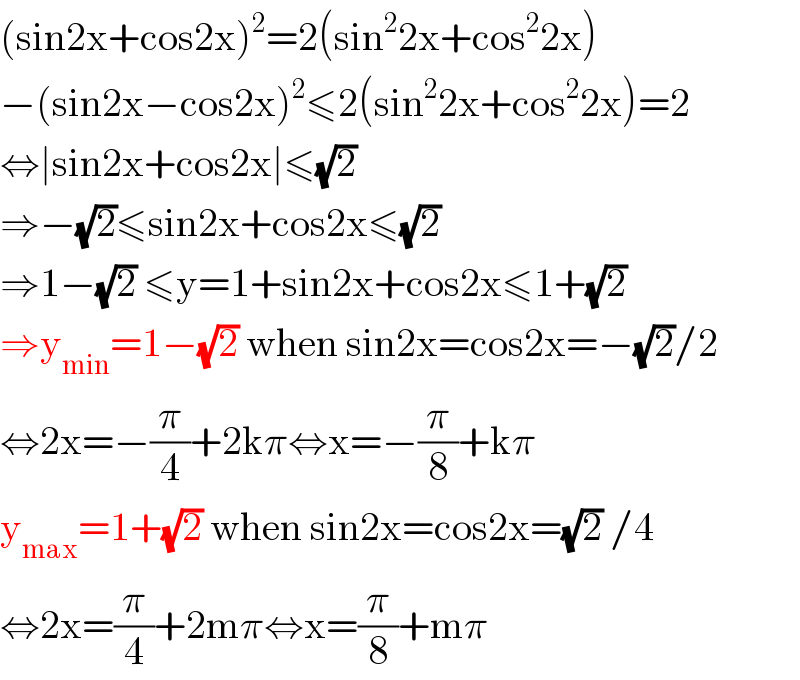
$$\left(\mathrm{sin2x}+\mathrm{cos2x}\right)^{\mathrm{2}} =\mathrm{2}\left(\mathrm{sin}^{\mathrm{2}} \mathrm{2x}+\mathrm{cos}^{\mathrm{2}} \mathrm{2x}\right) \\ $$$$−\left(\mathrm{sin2x}−\mathrm{cos2x}\right)^{\mathrm{2}} \leqslant\mathrm{2}\left(\mathrm{sin}^{\mathrm{2}} \mathrm{2x}+\mathrm{cos}^{\mathrm{2}} \mathrm{2x}\right)=\mathrm{2} \\ $$$$\Leftrightarrow\mid\mathrm{sin2x}+\mathrm{cos2x}\mid\leqslant\sqrt{\mathrm{2}}\: \\ $$$$\Rightarrow−\sqrt{\mathrm{2}}\leqslant\mathrm{sin2x}+\mathrm{cos2x}\leqslant\sqrt{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{1}−\sqrt{\mathrm{2}}\:\leqslant\mathrm{y}=\mathrm{1}+\mathrm{sin2x}+\mathrm{cos2x}\leqslant\mathrm{1}+\sqrt{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{y}_{\mathrm{min}} =\mathrm{1}−\sqrt{\mathrm{2}}\:\mathrm{when}\:\mathrm{sin2x}=\mathrm{cos2x}=−\sqrt{\mathrm{2}}/\mathrm{2} \\ $$$$\Leftrightarrow\mathrm{2x}=−\frac{\pi}{\mathrm{4}}+\mathrm{2k}\pi\Leftrightarrow\mathrm{x}=−\frac{\pi}{\mathrm{8}}+\mathrm{k}\pi \\ $$$$\mathrm{y}_{\mathrm{max}} =\mathrm{1}+\sqrt{\mathrm{2}}\:\mathrm{when}\:\mathrm{sin2x}=\mathrm{cos2x}=\sqrt{\mathrm{2}}\:/\mathrm{4} \\ $$$$\Leftrightarrow\mathrm{2x}=\frac{\pi}{\mathrm{4}}+\mathrm{2m}\pi\Leftrightarrow\mathrm{x}=\frac{\pi}{\mathrm{8}}+\mathrm{m}\pi \\ $$
