Question Number 123878 by liberty last updated on 29/Nov/20

$${Nine}\:{chairs}\:{in}\:{a}\:{row}\:{are}\:{to}\:{be}\:{occupied}\:{by} \\ $$$${six}\:{students}\:{and}\:{Prof}\:{George}\:,\:{Prof}\:{Pieter}, \\ $$$${and}\:{Prof}\:{John}.\:{These}\:{three}\:{professors}\:{arrive} \\ $$$${before}\:{the}\:{six}\:{students}\:{and}\:{decide}\:{to}\:{choose} \\ $$$${their}\:{chairs}\:{so}\:{that}\:{each}\:{professor}\:{will}\:{be}\:{between} \\ $$$${two}\:{students}.\:{In}\:{how}\:{many}\:{ways}\:{can}\:{Professor}\:{George} \\ $$$$,\:{Pieter}\:{and}\:{John}\:{choose}\:{their}\:{chairs}\:?\: \\ $$
Answered by john_santu last updated on 29/Nov/20
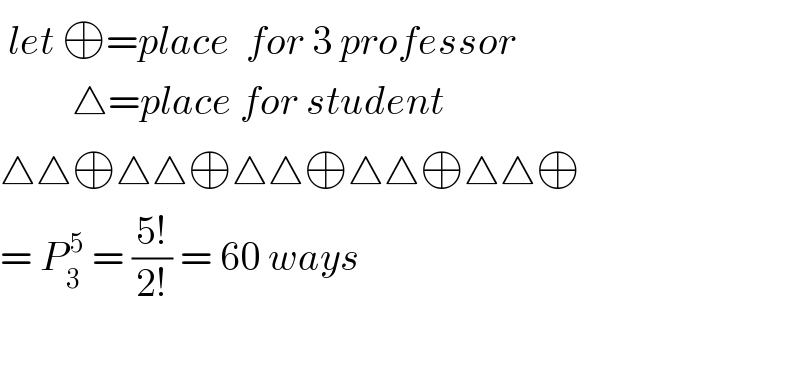
$$\:{let}\:\oplus={place}\:\:{for}\:\mathrm{3}\:{professor} \\ $$$$\:\:\:\:\:\:\:\:\:\bigtriangleup={place}\:{for}\:{student} \\ $$$$\bigtriangleup\bigtriangleup\oplus\bigtriangleup\bigtriangleup\oplus\bigtriangleup\bigtriangleup\oplus\bigtriangleup\bigtriangleup\oplus\bigtriangleup\bigtriangleup\oplus \\ $$$$=\:{P}_{\mathrm{3}} ^{\:\mathrm{5}} \:=\:\frac{\mathrm{5}!}{\mathrm{2}!}\:=\:\mathrm{60}\:{ways} \\ $$$$ \\ $$
