Question Number 36814 by MJS last updated on 06/Jun/18
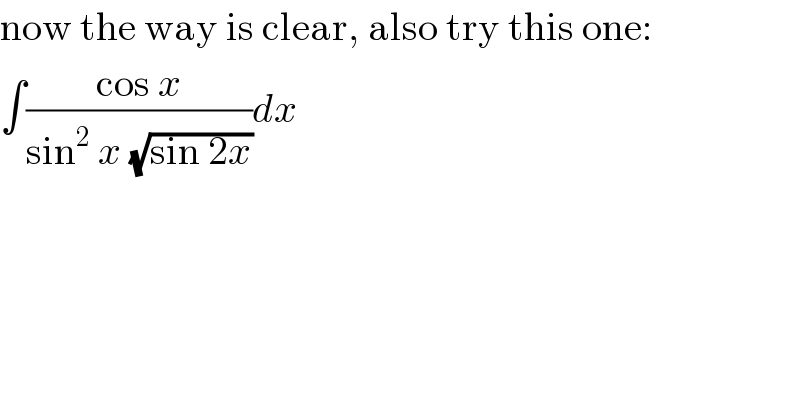
$$\mathrm{now}\:\mathrm{the}\:\mathrm{way}\:\mathrm{is}\:\mathrm{clear},\:\mathrm{also}\:\mathrm{try}\:\mathrm{this}\:\mathrm{one}: \\ $$$$\int\frac{\mathrm{cos}\:{x}}{\mathrm{sin}^{\mathrm{2}} \:{x}\:\sqrt{\mathrm{sin}\:\mathrm{2}{x}}}{dx} \\ $$
Answered by math1967 last updated on 06/Jun/18
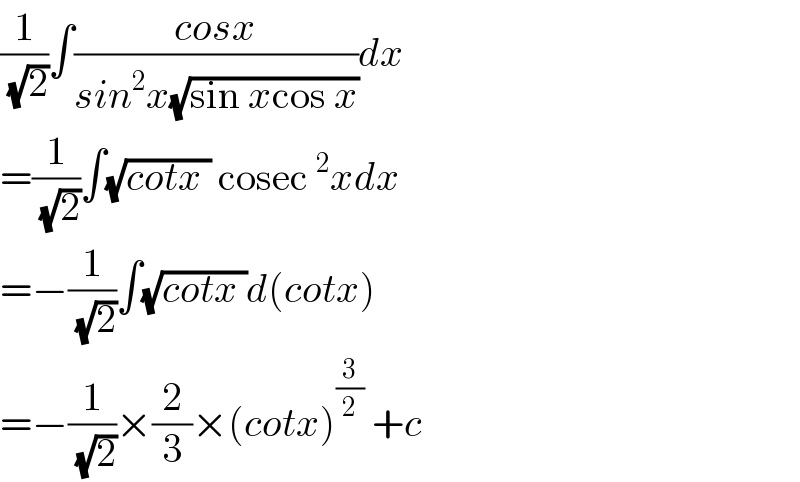
$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{{cosx}}{{sin}^{\mathrm{2}} {x}\sqrt{\mathrm{sin}\:{x}\mathrm{cos}\:{x}}}{dx} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\sqrt{{cotx}\:}\:\mathrm{cosec}\:^{\mathrm{2}} {xdx} \\ $$$$=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\sqrt{{cotx}\:}{d}\left({cotx}\right) \\ $$$$=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}×\frac{\mathrm{2}}{\mathrm{3}}×\left({cotx}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:+{c} \\ $$
