Menu Close

Number-of-distributions-of-12-different-things-be-taken-to-3different-boxes-so-as-1-5-things-in-1st-box-exactly-2-5-things-in-any-one-box-

Tinku Tara 0 Comments
Pin




Question Number 179738 by SLVR last updated on 01/Nov/22
Number of distributions of 12 different things be taken to 3different boxes so as 1)5 things in 1st box exactly 2)5 things in any one box?
$${Number}\:{of}\:{distributions}\:{of} \\ $$$$\mathrm{12}\:{different}\:{things}\:{be}\:{taken}\:{to} \\ $$$$\mathrm{3}{different}\:{boxes}\:{so}\:{as} \\ $$$$\left.\mathrm{1}\right)\mathrm{5}\:{things}\:{in}\:\mathrm{1}{st}\:{box}\:{exactly} \\ $$$$\left.\mathrm{2}\right)\mathrm{5}\:{things}\:{in}\:{any}\:{one}\:{box}? \\ $$
Answered by SLVR last updated on 01/Nov/22
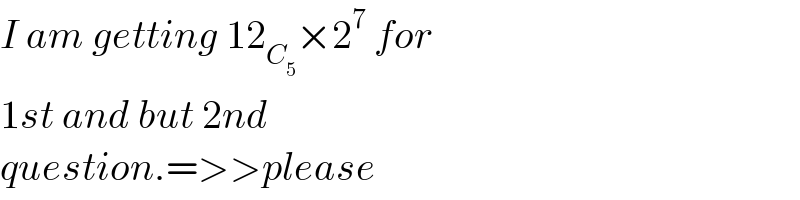
I am getting 12_C_5 ×2^7 for 1st and but 2nd question.=>>please
$${I}\:{am}\:{getting}\:\mathrm{12}_{{C}_{\mathrm{5}} } ×\mathrm{2}^{\mathrm{7}} \:{for} \\ $$$$\mathrm{1}{st}\:{and}\:{but}\:\mathrm{2}{nd} \\ $$$${question}.=>>{please} \\ $$
Answered by mr W last updated on 03/Nov/22
1) 5 things for the 1st box: C_5 ^(12) 7 things into two boxes: 2^7 ⇒C_5 ^(12) ×2^7 =101376 2) not clear, what you mean. at least or at most or exactly 5 things in one of the three boxes?
$$\left.\mathrm{1}\right) \\ $$$$\mathrm{5}\:{things}\:{for}\:{the}\:\mathrm{1}{st}\:{box}:\:{C}_{\mathrm{5}} ^{\mathrm{12}} \\ $$$$\mathrm{7}\:{things}\:{into}\:{two}\:{boxes}:\:\mathrm{2}^{\mathrm{7}} \\ $$$$\Rightarrow{C}_{\mathrm{5}} ^{\mathrm{12}} ×\mathrm{2}^{\mathrm{7}} =\mathrm{101376} \\ $$$$\left.\mathrm{2}\right) \\ $$$${not}\:{clear},\:\:{what}\:{you}\:{mean}. \\ $$$${at}\:{least}\:{or}\:{at}\:{most}\:{or}\:{exactly}\:\mathrm{5}\:{things} \\ $$$${in}\:{one}\:{of}\:{the}\:{three}\:{boxes}? \\ $$
Commented by SLVR last updated on 02/Nov/22
sir..so kind of you.. here in 2nd i need 5 exactly but what if a)if at least one in 2nd box? b)if at most 7 in 2nd box please sir Prof.Mr.W
$${sir}..{so}\:{kind}\:{of}\:{you}.. \\ $$$${here}\:{in}\:\mathrm{2}{nd}\:{i}\:{need}\:\mathrm{5}\:{exactly} \\ $$$$\left.{but}\:{what}\:{if}\:\:\:\:{a}\right){if}\:{at}\:{least}\:{one} \\ $$$${in}\:\mathrm{2}{nd}\:{box}? \\ $$$$\left.{b}\right){if}\:\:{at}\:{most}\:\mathrm{7}\:{in}\:\mathrm{2}{nd}\:{box} \\ $$$${please}\:{sir}\:{Prof}.{Mr}.{W} \\ $$
Commented by mr W last updated on 03/Nov/22
2a) say in one and only one box there are exactly 5 balls. to divide 12 balls into three boxes there are following possibilities: 5+0+7 ✓ ⇒((12!)/(5!7!))×3! 5+1+6 ✓ ⇒((12!)/(5!6!))×3! 5+2+5 × 5+3+4 ✓ ⇒((12!)/(5!3!4!))×3! ⇒answer is ((12!3!)/(5!))×((1/(7!))+(1/(6!))+(1/(3!4!)))=204 336
$$\left.\mathrm{2}{a}\right) \\ $$$${say}\:{in}\:{one}\:{and}\:{only}\:{one}\:{box}\:{there}\:{are} \\ $$$${exactly}\:\mathrm{5}\:{balls}. \\ $$$${to}\:{divide}\:\mathrm{12}\:{balls}\:{into}\:{three}\:{boxes} \\ $$$${there}\:{are}\:{following}\:{possibilities}: \\ $$$$\mathrm{5}+\mathrm{0}+\mathrm{7}\:\checkmark\:\Rightarrow\frac{\mathrm{12}!}{\mathrm{5}!\mathrm{7}!}×\mathrm{3}! \\ $$$$\mathrm{5}+\mathrm{1}+\mathrm{6}\:\checkmark\:\Rightarrow\frac{\mathrm{12}!}{\mathrm{5}!\mathrm{6}!}×\mathrm{3}! \\ $$$$\mathrm{5}+\mathrm{2}+\mathrm{5}\:× \\ $$$$\mathrm{5}+\mathrm{3}+\mathrm{4}\:\checkmark\:\Rightarrow\frac{\mathrm{12}!}{\mathrm{5}!\mathrm{3}!\mathrm{4}!}×\mathrm{3}! \\ $$$$\Rightarrow{answer}\:{is}\: \\ $$$$\:\:\:\:\frac{\mathrm{12}!\mathrm{3}!}{\mathrm{5}!}×\left(\frac{\mathrm{1}}{\mathrm{7}!}+\frac{\mathrm{1}}{\mathrm{6}!}+\frac{\mathrm{1}}{\mathrm{3}!\mathrm{4}!}\right)=\mathrm{204}\:\mathrm{336} \\ $$
Commented by mr W last updated on 03/Nov/22
2b) say in one box at least 5 balls: 12+0+0⇒1×((3!)/(2!))=3 11+1+0 ⇒((12!)/(11!))×3!=72 10+2+0 ⇒((12!)/(10!2!))×3!=396 10+1+1 ⇒((12!)/(10!2!))×3!=396 9+3+0 ⇒((12!)/(9!3!))×3!=1 320 9+2+1 ⇒((12!)/(9!2!))×3!=3 960 8+4+0 ⇒((12!)/(8!4!))×3!=2 970 8+3+1 ⇒((12!)/(8!3!))×3!=11 880 8+2+2 ⇒((12!)/(8!(2!)^2 2!))×3!=8 910 7+5+0 ⇒((12!)/(7!5!))×3!=4 752 7+4+1 ⇒((12!)/(7!4!))×3!=23 760 7+3+2 ⇒((12!)/(7!3!2!))×3!=47 520 6+6+0 ⇒((12!)/((6!)^2 2!))×3!=2 772 6+5+1 ⇒((12!)/(6!5!))×3!=33 264 6+4+2 ⇒((12!)/(6!4!2!))×3!=83 160 6+3+3 ⇒((12!)/(6!(3!)^2 2!))×3!=55 440 5+5+2 ⇒((12!)/((5!)^2 2!2!))×3!=49896 5+4+3 ⇒((12!)/(5!4!3!))×3!=166 320 totally: 496 791
$$\left.\mathrm{2}{b}\right) \\ $$$${say}\:{in}\:{one}\:{box}\:{at}\:{least}\:\mathrm{5}\:{balls}: \\ $$$$\mathrm{12}+\mathrm{0}+\mathrm{0}\Rightarrow\mathrm{1}×\frac{\mathrm{3}!}{\mathrm{2}!}=\mathrm{3} \\ $$$$\mathrm{11}+\mathrm{1}+\mathrm{0}\:\Rightarrow\frac{\mathrm{12}!}{\mathrm{11}!}×\mathrm{3}!=\mathrm{72} \\ $$$$\mathrm{10}+\mathrm{2}+\mathrm{0}\:\Rightarrow\frac{\mathrm{12}!}{\mathrm{10}!\mathrm{2}!}×\mathrm{3}!=\mathrm{396} \\ $$$$\mathrm{10}+\mathrm{1}+\mathrm{1}\:\Rightarrow\frac{\mathrm{12}!}{\mathrm{10}!\mathrm{2}!}×\mathrm{3}!=\mathrm{396} \\ $$$$\mathrm{9}+\mathrm{3}+\mathrm{0}\:\Rightarrow\frac{\mathrm{12}!}{\mathrm{9}!\mathrm{3}!}×\mathrm{3}!=\mathrm{1}\:\mathrm{320} \\ $$$$\mathrm{9}+\mathrm{2}+\mathrm{1}\:\Rightarrow\frac{\mathrm{12}!}{\mathrm{9}!\mathrm{2}!}×\mathrm{3}!=\mathrm{3}\:\mathrm{960} \\ $$$$\mathrm{8}+\mathrm{4}+\mathrm{0}\:\Rightarrow\frac{\mathrm{12}!}{\mathrm{8}!\mathrm{4}!}×\mathrm{3}!=\mathrm{2}\:\mathrm{970} \\ $$$$\mathrm{8}+\mathrm{3}+\mathrm{1}\:\Rightarrow\frac{\mathrm{12}!}{\mathrm{8}!\mathrm{3}!}×\mathrm{3}!=\mathrm{11}\:\mathrm{880} \\ $$$$\mathrm{8}+\mathrm{2}+\mathrm{2}\:\:\Rightarrow\frac{\mathrm{12}!}{\mathrm{8}!\left(\mathrm{2}!\right)^{\mathrm{2}} \mathrm{2}!}×\mathrm{3}!=\mathrm{8}\:\mathrm{910} \\ $$$$\mathrm{7}+\mathrm{5}+\mathrm{0}\:\Rightarrow\frac{\mathrm{12}!}{\mathrm{7}!\mathrm{5}!}×\mathrm{3}!=\mathrm{4}\:\mathrm{752} \\ $$$$\mathrm{7}+\mathrm{4}+\mathrm{1}\:\Rightarrow\frac{\mathrm{12}!}{\mathrm{7}!\mathrm{4}!}×\mathrm{3}!=\mathrm{23}\:\mathrm{760} \\ $$$$\mathrm{7}+\mathrm{3}+\mathrm{2}\:\Rightarrow\frac{\mathrm{12}!}{\mathrm{7}!\mathrm{3}!\mathrm{2}!}×\mathrm{3}!=\mathrm{47}\:\mathrm{520} \\ $$$$\mathrm{6}+\mathrm{6}+\mathrm{0}\:\Rightarrow\frac{\mathrm{12}!}{\left(\mathrm{6}!\right)^{\mathrm{2}} \mathrm{2}!}×\mathrm{3}!=\mathrm{2}\:\mathrm{772} \\ $$$$\mathrm{6}+\mathrm{5}+\mathrm{1}\:\Rightarrow\frac{\mathrm{12}!}{\mathrm{6}!\mathrm{5}!}×\mathrm{3}!=\mathrm{33}\:\mathrm{264} \\ $$$$\mathrm{6}+\mathrm{4}+\mathrm{2}\:\Rightarrow\frac{\mathrm{12}!}{\mathrm{6}!\mathrm{4}!\mathrm{2}!}×\mathrm{3}!=\mathrm{83}\:\mathrm{160} \\ $$$$\mathrm{6}+\mathrm{3}+\mathrm{3}\:\Rightarrow\frac{\mathrm{12}!}{\mathrm{6}!\left(\mathrm{3}!\right)^{\mathrm{2}} \mathrm{2}!}×\mathrm{3}!=\mathrm{55}\:\mathrm{440} \\ $$$$\mathrm{5}+\mathrm{5}+\mathrm{2}\:\Rightarrow\frac{\mathrm{12}!}{\left(\mathrm{5}!\right)^{\mathrm{2}} \mathrm{2}!\mathrm{2}!}×\mathrm{3}!=\mathrm{49896} \\ $$$$\mathrm{5}+\mathrm{4}+\mathrm{3}\:\Rightarrow\frac{\mathrm{12}!}{\mathrm{5}!\mathrm{4}!\mathrm{3}!}×\mathrm{3}!=\mathrm{166}\:\mathrm{320} \\ $$$${totally}:\:\:\mathrm{496}\:\mathrm{791} \\ $$
Commented by SLVR last updated on 02/Nov/22
Now...i got the clarity..so kind of sir..thanks a lot
$${Now}…{i}\:{got}\:{the}\:{clarity}..{so} \\ $$$${kind}\:{of}\:{sir}..{thanks}\:{a}\:{lot} \\ $$
Commented by mr W last updated on 03/Nov/22
generating functions are powerful tools for solving such questions. we don′t need to enumerate the concrete combinations as i did above. examples: 1) coef. of term x^(12) in 12!×(x^5 /(5!))×(e^x )^2 which is 101 376.
$${generating}\:{functions}\:{are}\:{powerful} \\ $$$${tools}\:{for}\:{solving}\:{such}\:{questions}. \\ $$$${we}\:{don}'{t}\:{need}\:{to}\:{enumerate}\:{the} \\ $$$${concrete}\:{combinations}\:{as}\:{i}\:{did}\:{above}. \\ $$$${examples}: \\ $$$$\left.\mathrm{1}\right) \\ $$$${coef}.\:{of}\:{term}\:{x}^{\mathrm{12}} \:{in} \\ $$$$\mathrm{12}!×\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}×\left({e}^{{x}} \right)^{\mathrm{2}} \\ $$$${which}\:{is}\:\mathrm{101}\:\mathrm{376}. \\ $$
Commented by mr W last updated on 03/Nov/22
Commented by mr W last updated on 03/Nov/22
2a) coef. of term x^(12) in 3×12!×(x^5 /(5!))×(e^x −(x^5 /(5!)))^2 which is 204 336.
$$\left.\mathrm{2}{a}\right) \\ $$$${coef}.\:{of}\:{term}\:{x}^{\mathrm{12}} \:{in} \\ $$$$\mathrm{3}×\mathrm{12}!×\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}×\left({e}^{{x}} −\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}\right)^{\mathrm{2}} \\ $$$${which}\:{is}\:\mathrm{204}\:\mathrm{336}. \\ $$
Commented by mr W last updated on 03/Nov/22
Commented by mr W last updated on 03/Nov/22
2b) without restriction: 3^(12) =531 441 ways all boxes have less than 5 balls, i.e. each has 4 balls: ((12!)/((4!)^3 ))=34650 ways one box has at least 5 balls: ⇒531 441−34 650=496 791 or using generating functions:
$$\left.\mathrm{2}{b}\right) \\ $$$${without}\:{restriction}:\:\mathrm{3}^{\mathrm{12}} =\mathrm{531}\:\mathrm{441}\:{ways} \\ $$$${all}\:{boxes}\:{have}\:{less}\:{than}\:\mathrm{5}\:{balls},\:{i}.{e}. \\ $$$${each}\:{has}\:\mathrm{4}\:{balls}:\:\frac{\mathrm{12}!}{\left(\mathrm{4}!\right)^{\mathrm{3}} }=\mathrm{34650}\:{ways} \\ $$$${one}\:{box}\:{has}\:{at}\:{least}\:\mathrm{5}\:{balls}: \\ $$$$\Rightarrow\mathrm{531}\:\mathrm{441}−\mathrm{34}\:\mathrm{650}=\mathrm{496}\:\mathrm{791} \\ $$$$ \\ $$$${or}\:{using}\:{generating}\:{functions}: \\ $$
Commented by mr W last updated on 03/Nov/22
Commented by mr W last updated on 03/Nov/22

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *