Question Number 15094 by Tinkutara last updated on 07/Jun/17
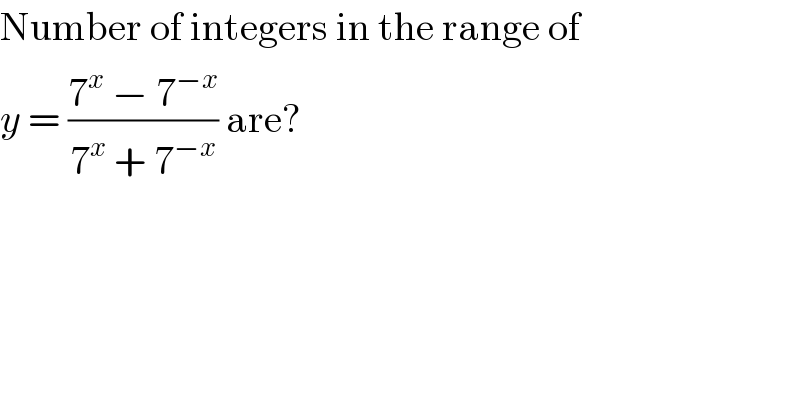
$$\mathrm{Number}\:\mathrm{of}\:\mathrm{integers}\:\mathrm{in}\:\mathrm{the}\:\mathrm{range}\:\mathrm{of} \\ $$$${y}\:=\:\frac{\mathrm{7}^{{x}} \:−\:\mathrm{7}^{−{x}} }{\mathrm{7}^{{x}} \:+\:\mathrm{7}^{−{x}} }\:\mathrm{are}? \\ $$
Answered by mrW1 last updated on 07/Jun/17
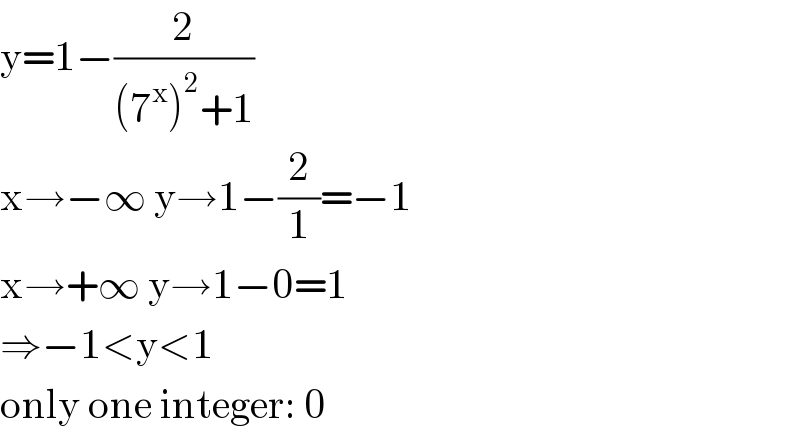
$$\mathrm{y}=\mathrm{1}−\frac{\mathrm{2}}{\left(\mathrm{7}^{\mathrm{x}} \right)^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{x}\rightarrow−\infty\:\mathrm{y}\rightarrow\mathrm{1}−\frac{\mathrm{2}}{\mathrm{1}}=−\mathrm{1} \\ $$$$\mathrm{x}\rightarrow+\infty\:\mathrm{y}\rightarrow\mathrm{1}−\mathrm{0}=\mathrm{1} \\ $$$$\Rightarrow−\mathrm{1}<\mathrm{y}<\mathrm{1} \\ $$$$\mathrm{only}\:\mathrm{one}\:\mathrm{integer}:\:\mathrm{0} \\ $$
Commented by Tinkutara last updated on 07/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
