Question Number 169863 by SANOGO last updated on 11/May/22
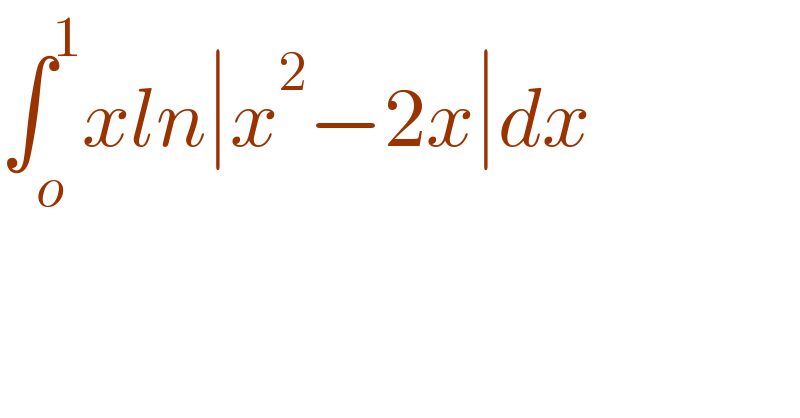
$$\int_{{o}} ^{\mathrm{1}} {xln}\mid{x}^{\mathrm{2}} −\mathrm{2}{x}\mid{dx} \\ $$
Answered by Mathspace last updated on 11/May/22
![x^2 −2x=x(x−2)<0 sur [01] ⇒ ∫_0 ^1 xln∣x^2 −2x∣dx= =∫_0 ^1 xln(2x−x^2 )dx =[(x^2 /2)ln(2x−x^2 )]_0 ^1 −∫_0 ^1 (x^2 /2)×((2−2x)/(2x−x^2 ))dx =o−∫_0 ^1 ((x^2 (1−x))/(2x−x^2 ))dx =−∫_0 ^1 ((x(1−x))/(2−x))dx =−∫_0 ^1 ((x−x^2 )/(2−x))dx=−∫_0 ^1 ((x^2 −x)/(x−2))dx =−∫_0 ^1 ((x^2 −4+4)/(x−2))dx =−∫_0 ^1 (x+2)dx−4∫_0 ^1 (dx/(x−2)) =−[ (x^2 /2)+2x]_0 ^1 −4[ln∣x−2∣]_0 ^1 =−((1/2)+2)−4(−ln(2)) =−(5/2)+4ln(2)](https://www.tinkutara.com/question/Q169866.png)
$${x}^{\mathrm{2}} −\mathrm{2}{x}={x}\left({x}−\mathrm{2}\right)<\mathrm{0}\:{sur}\:\left[\mathrm{01}\right]\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {xln}\mid{x}^{\mathrm{2}} −\mathrm{2}{x}\mid{dx}= \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {xln}\left(\mathrm{2}{x}−{x}^{\mathrm{2}} \right){dx} \\ $$$$=\left[\frac{{x}^{\mathrm{2}} }{\mathrm{2}}{ln}\left(\mathrm{2}{x}−{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} }{\mathrm{2}}×\frac{\mathrm{2}−\mathrm{2}{x}}{\mathrm{2}{x}−{x}^{\mathrm{2}} }{dx} \\ $$$$={o}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)}{\mathrm{2}{x}−{x}^{\mathrm{2}} }{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}\left(\mathrm{1}−{x}\right)}{\mathrm{2}−{x}}{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}−{x}^{\mathrm{2}} }{\mathrm{2}−{x}}{dx}=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} −{x}}{{x}−\mathrm{2}}{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} −\mathrm{4}+\mathrm{4}}{{x}−\mathrm{2}}{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \left({x}+\mathrm{2}\right){dx}−\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{{x}−\mathrm{2}} \\ $$$$=−\left[\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2}{x}\right]_{\mathrm{0}} ^{\mathrm{1}} −\mathrm{4}\left[{ln}\mid{x}−\mathrm{2}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=−\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{2}\right)−\mathrm{4}\left(−{ln}\left(\mathrm{2}\right)\right) \\ $$$$=−\frac{\mathrm{5}}{\mathrm{2}}+\mathrm{4}{ln}\left(\mathrm{2}\right) \\ $$
