Question Number 109086 by bobhans last updated on 21/Aug/20
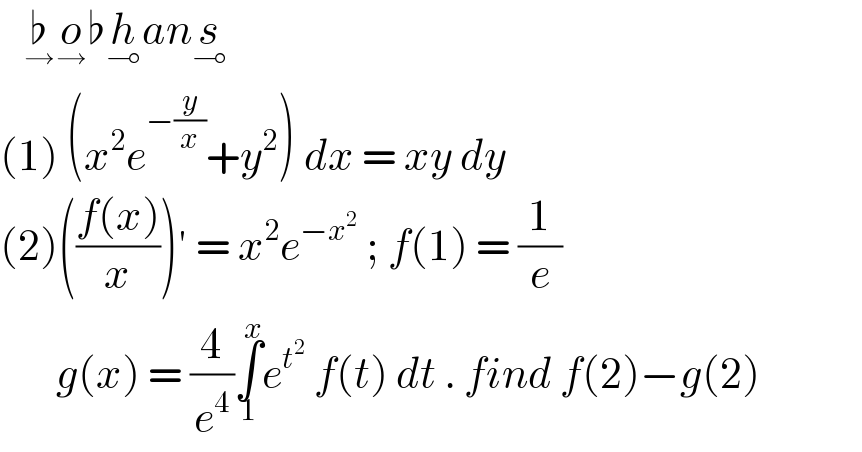
$$\:\:\:\underset{\rightarrow} {\flat}\underset{\rightarrow} {{o}}\flat\underset{\multimap} {{h}an}\underset{\multimap} {{s}} \\ $$$$\left(\mathrm{1}\right)\:\left({x}^{\mathrm{2}} {e}^{−\frac{{y}}{{x}}} +{y}^{\mathrm{2}} \right)\:{dx}\:=\:{xy}\:{dy}\: \\ $$$$\left(\mathrm{2}\right)\left(\frac{{f}\left({x}\right)}{{x}}\right)'\:=\:{x}^{\mathrm{2}} {e}^{−{x}^{\mathrm{2}} } \:;\:{f}\left(\mathrm{1}\right)\:=\:\frac{\mathrm{1}}{{e}}\: \\ $$$$\:\:\:\:\:\:\:{g}\left({x}\right)\:=\:\frac{\mathrm{4}}{{e}^{\mathrm{4}} }\underset{\mathrm{1}} {\overset{{x}} {\int}}{e}^{{t}^{\mathrm{2}} } \:{f}\left({t}\right)\:{dt}\:.\:{find}\:{f}\left(\mathrm{2}\right)−{g}\left(\mathrm{2}\right) \\ $$
Answered by bemath last updated on 21/Aug/20
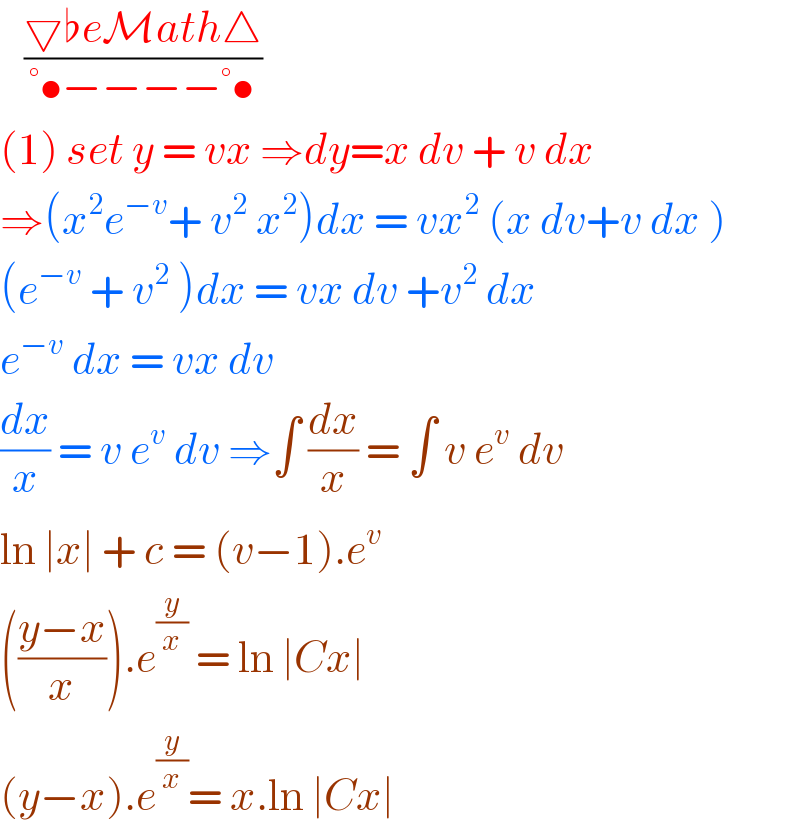
$$\:\:\:\frac{\bigtriangledown\flat{e}\mathcal{M}{ath}\bigtriangleup}{°\bullet−−−−°\bullet} \\ $$$$\left(\mathrm{1}\right)\:{set}\:{y}\:=\:{vx}\:\Rightarrow{dy}={x}\:{dv}\:+\:{v}\:{dx} \\ $$$$\Rightarrow\left({x}^{\mathrm{2}} {e}^{−{v}} +\:{v}^{\mathrm{2}} \:{x}^{\mathrm{2}} \right){dx}\:=\:{vx}^{\mathrm{2}} \:\left({x}\:{dv}+{v}\:{dx}\:\right) \\ $$$$\left({e}^{−{v}} \:+\:{v}^{\mathrm{2}} \:\right){dx}\:=\:{vx}\:{dv}\:+{v}^{\mathrm{2}} \:{dx} \\ $$$${e}^{−{v}} \:{dx}\:=\:{vx}\:{dv}\: \\ $$$$\frac{{dx}}{{x}}\:=\:{v}\:{e}^{{v}} \:{dv}\:\Rightarrow\int\:\frac{{dx}}{{x}}\:=\:\int\:{v}\:{e}^{{v}} \:{dv}\: \\ $$$$\mathrm{ln}\:\mid{x}\mid\:+\:{c}\:=\:\left({v}−\mathrm{1}\right).{e}^{{v}} \\ $$$$\left(\frac{{y}−{x}}{{x}}\right).{e}^{\frac{{y}}{{x}}} \:=\:\mathrm{ln}\:\mid{Cx}\mid\: \\ $$$$\left({y}−{x}\right).{e}^{\frac{{y}}{{x}}} =\:{x}.\mathrm{ln}\:\mid{Cx}\mid\: \\ $$
