Menu Close

o-hans-x-3-x-2-y-9-y-3-y-2-x-25-find-x-and-y-

Tinku Tara 0 Comments
Pin




Question Number 109237 by bobhans last updated on 22/Aug/20
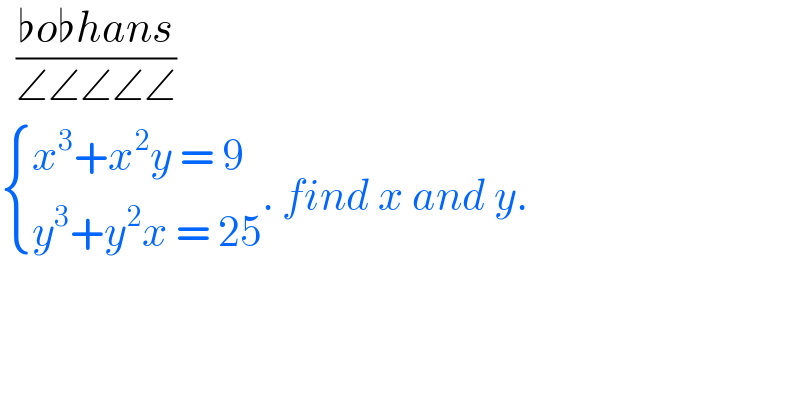
((♭o♭hans)/(∠∠∠∠∠)) { ((x^3 +x^2 y = 9)),((y^3 +y^2 x = 25)) :}. find x and y.
$$\:\:\frac{\flat{o}\flat{hans}}{\angle\angle\angle\angle\angle} \\ $$$$\begin{cases}{{x}^{\mathrm{3}} +{x}^{\mathrm{2}} {y}\:=\:\mathrm{9}}\\{{y}^{\mathrm{3}} +{y}^{\mathrm{2}} {x}\:=\:\mathrm{25}}\end{cases}.\:{find}\:{x}\:{and}\:{y}. \\ $$
Answered by bemath last updated on 22/Aug/20
((∠♭emath∼)/(−−−−−−)) { ((x^2 (x+y)=9)),((y^2 (x+y) = 25)) :} → { ((x(√(x+y)) = 3)),((y(√(x+y)) = 5)) :} ⇒(x+y)(√(x+y)) = 8 ⇒((√(x+y)))^3 = 8 (√(x+y)) = 2 so we get { ((4x^2 = 9)),((4y^2 = 25)) :} since the original equation x^2 (x+y)=9 > 0 it must be → { ((x>0)),((y>0)) :} the solution is {(3/2), (5/2)}
$$\:\:\:\frac{\angle\flat{emath}\sim}{−−−−−−} \\ $$$$\begin{cases}{{x}^{\mathrm{2}} \left({x}+{y}\right)=\mathrm{9}}\\{{y}^{\mathrm{2}} \left({x}+{y}\right)\:=\:\mathrm{25}}\end{cases}\:\rightarrow\begin{cases}{{x}\sqrt{{x}+{y}}\:=\:\mathrm{3}}\\{{y}\sqrt{{x}+{y}}\:=\:\mathrm{5}}\end{cases} \\ $$$$\Rightarrow\left({x}+{y}\right)\sqrt{{x}+{y}}\:=\:\mathrm{8}\:\Rightarrow\left(\sqrt{{x}+{y}}\right)^{\mathrm{3}} \:=\:\mathrm{8} \\ $$$$\sqrt{{x}+{y}}\:=\:\mathrm{2}\:{so}\:{we}\:{get}\:\begin{cases}{\mathrm{4}{x}^{\mathrm{2}} \:=\:\mathrm{9}}\\{\mathrm{4}{y}^{\mathrm{2}} \:=\:\mathrm{25}}\end{cases} \\ $$$${since}\:{the}\:{original}\:{equation}\: \\ $$$${x}^{\mathrm{2}} \left({x}+{y}\right)=\mathrm{9}\:>\:\mathrm{0}\:{it}\:{must}\:{be}\:\rightarrow\begin{cases}{{x}>\mathrm{0}}\\{{y}>\mathrm{0}}\end{cases} \\ $$$${the}\:{solution}\:{is}\:\left\{\frac{\mathrm{3}}{\mathrm{2}},\:\frac{\mathrm{5}}{\mathrm{2}}\right\} \\ $$
Commented by bobhans last updated on 22/Aug/20
ccollll....max
$${ccollll}….{max} \\ $$
Commented by Rasheed.Sindhi last updated on 22/Aug/20
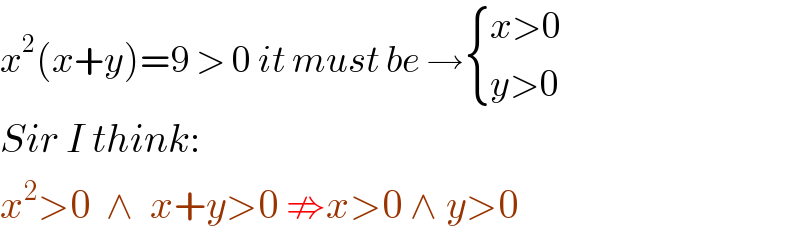
x^2 (x+y)=9 > 0 it must be → { ((x>0)),((y>0)) :} Sir I think: x^2 >0 ∧ x+y>0 ⇏x>0 ∧ y>0
$${x}^{\mathrm{2}} \left({x}+{y}\right)=\mathrm{9}\:>\:\mathrm{0}\:{it}\:{must}\:{be}\:\rightarrow\begin{cases}{{x}>\mathrm{0}}\\{{y}>\mathrm{0}}\end{cases} \\ $$$${Sir}\:{I}\:{think}: \\ $$$${x}^{\mathrm{2}} >\mathrm{0}\:\:\wedge\:\:{x}+{y}>\mathrm{0}\:\nRightarrow{x}>\mathrm{0}\:\wedge\:{y}>\mathrm{0} \\ $$
Commented by bemath last updated on 22/Aug/20
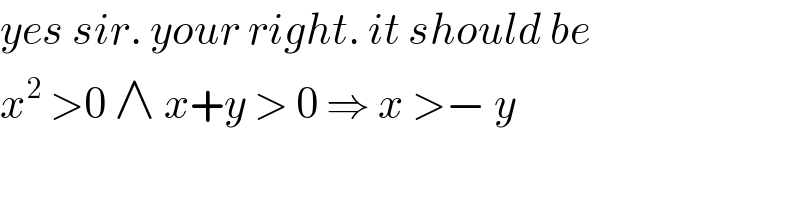
yes sir. your right. it should be x^2 >0 ∧ x+y > 0 ⇒ x >− y
$${yes}\:{sir}.\:{your}\:{right}.\:{it}\:{should}\:{be} \\ $$$${x}^{\mathrm{2}} \:>\mathrm{0}\:\wedge\:{x}+{y}\:>\:\mathrm{0}\:\Rightarrow\:{x}\:>−\:{y}\: \\ $$
Commented by Rasheed.Sindhi last updated on 22/Aug/20
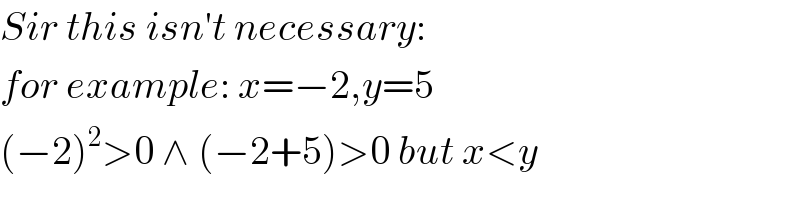
Sir this isn′t necessary: for example: x=−2,y=5 (−2)^2 >0 ∧ (−2+5)>0 but x<y
$${Sir}\:{this}\:{isn}'{t}\:{necessary}: \\ $$$${for}\:{example}:\:{x}=−\mathrm{2},{y}=\mathrm{5} \\ $$$$\left(−\mathrm{2}\right)^{\mathrm{2}} >\mathrm{0}\:\wedge\:\left(−\mathrm{2}+\mathrm{5}\right)>\mathrm{0}\:{but}\:{x}<{y} \\ $$
Commented by bemath last updated on 22/Aug/20
hahaha..typo sir
$${hahaha}..{typo}\:{sir} \\ $$$$ \\ $$
Commented by Rasheed.Sindhi last updated on 22/Aug/20
♥∣⟨ $!┌
$$\heartsuit\mid\langle\:\:\$!\ulcorner \\ $$
Commented by Aziztisffola last updated on 22/Aug/20
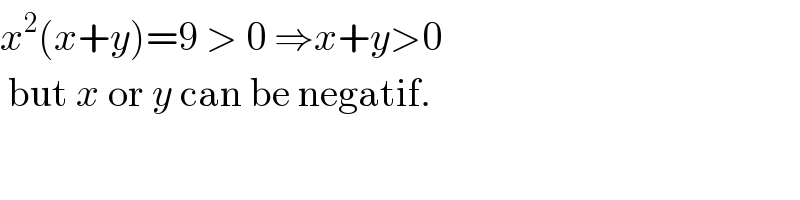
x^2 (x+y)=9 > 0 ⇒x+y>0 but x or y can be negatif.
$${x}^{\mathrm{2}} \left({x}+{y}\right)=\mathrm{9}\:>\:\mathrm{0}\:\Rightarrow{x}+{y}>\mathrm{0} \\ $$$$\:\mathrm{but}\:{x}\:\mathrm{or}\:{y}\:\mathrm{can}\:\mathrm{be}\:\mathrm{negatif}. \\ $$
Answered by Rasheed.Sindhi last updated on 22/Aug/20
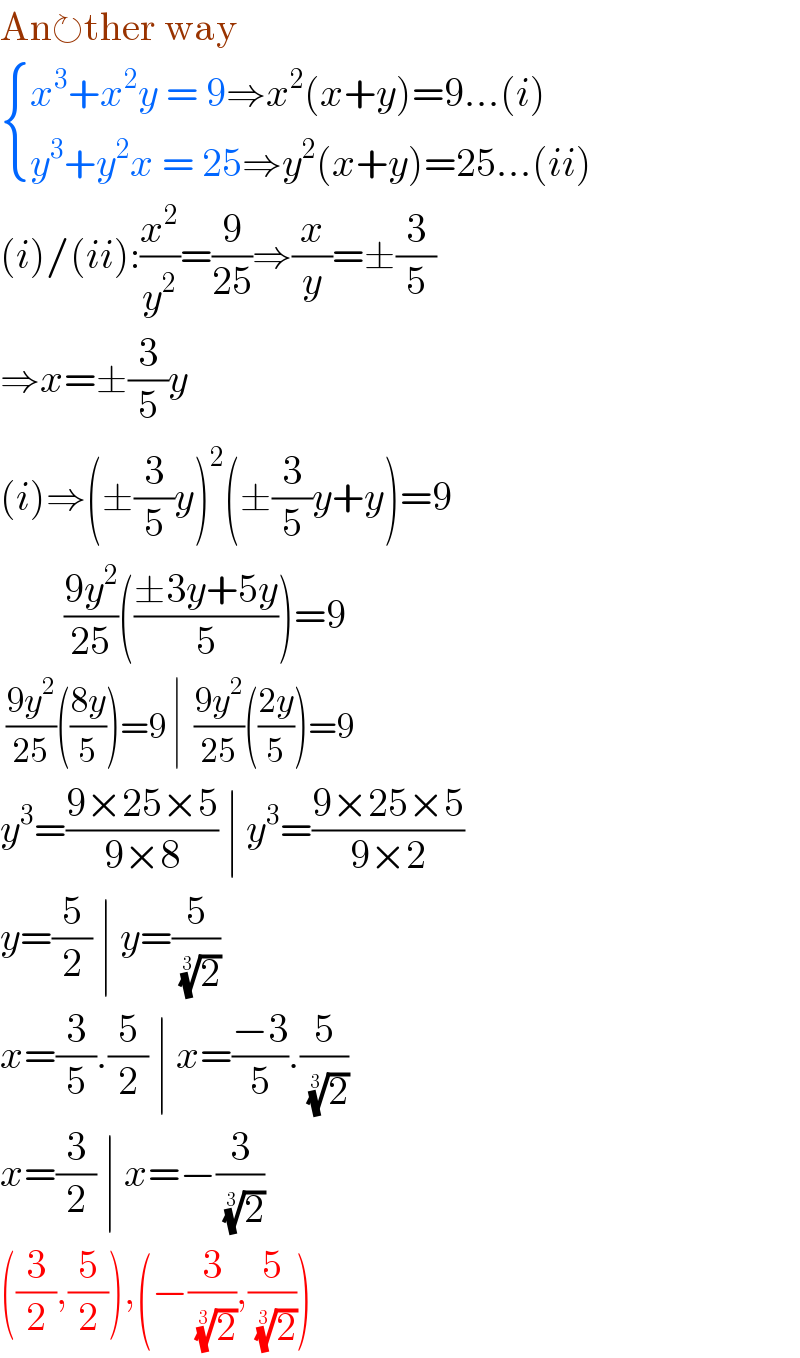
An↻ther way { ((x^3 +x^2 y = 9⇒x^2 (x+y)=9...(i))),((y^3 +y^2 x = 25⇒y^2 (x+y)=25...(ii))) :} (i)/(ii):(x^2 /y^2 )=(9/(25))⇒(x/y)=±(3/5) ⇒x=±(3/5)y (i)⇒(±(3/5)y)^2 (±(3/5)y+y)=9 ((9y^2 )/(25))(((±3y+5y)/5))=9 ((9y^2 )/(25))(((8y)/5))=9 ∣ ((9y^2 )/(25))(((2y)/5))=9 y^3 =((9×25×5)/(9×8)) ∣ y^3 =((9×25×5)/(9×2)) y=(5/2) ∣ y=(5/( (2)^(1/3) )) x=(3/5).(5/2) ∣ x=((−3)/5).(5/( (2)^(1/3) )) x=(3/2) ∣ x=−(3/( (2)^(1/3) )) ((3/2),(5/2)),(−(3/( (2)^(1/3) )),(5/( (2)^(1/3) )))
$$\mathrm{An}\circlearrowright\mathrm{ther}\:\mathrm{way} \\ $$$$\begin{cases}{{x}^{\mathrm{3}} +{x}^{\mathrm{2}} {y}\:=\:\mathrm{9}\Rightarrow{x}^{\mathrm{2}} \left({x}+{y}\right)=\mathrm{9}…\left({i}\right)}\\{{y}^{\mathrm{3}} +{y}^{\mathrm{2}} {x}\:=\:\mathrm{25}\Rightarrow{y}^{\mathrm{2}} \left({x}+{y}\right)=\mathrm{25}…\left({ii}\right)}\end{cases} \\ $$$$\left({i}\right)/\left({ii}\right):\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} }=\frac{\mathrm{9}}{\mathrm{25}}\Rightarrow\frac{{x}}{{y}}=\pm\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\Rightarrow{x}=\pm\frac{\mathrm{3}}{\mathrm{5}}{y} \\ $$$$\left({i}\right)\Rightarrow\left(\pm\frac{\mathrm{3}}{\mathrm{5}}{y}\right)^{\mathrm{2}} \left(\pm\frac{\mathrm{3}}{\mathrm{5}}{y}+{y}\right)=\mathrm{9} \\ $$$$\:\:\:\:\:\:\:\:\frac{\mathrm{9}{y}^{\mathrm{2}} }{\mathrm{25}}\left(\frac{\pm\mathrm{3}{y}+\mathrm{5}{y}}{\mathrm{5}}\right)=\mathrm{9} \\ $$$$\:\frac{\mathrm{9}{y}^{\mathrm{2}} }{\mathrm{25}}\left(\frac{\mathrm{8}{y}}{\mathrm{5}}\right)=\mathrm{9}\:\mid\:\:\frac{\mathrm{9}{y}^{\mathrm{2}} }{\mathrm{25}}\left(\frac{\mathrm{2}{y}}{\mathrm{5}}\right)=\mathrm{9} \\ $$$${y}^{\mathrm{3}} =\frac{\mathrm{9}×\mathrm{25}×\mathrm{5}}{\mathrm{9}×\mathrm{8}}\:\mid\:{y}^{\mathrm{3}} =\frac{\mathrm{9}×\mathrm{25}×\mathrm{5}}{\mathrm{9}×\mathrm{2}} \\ $$$${y}=\frac{\mathrm{5}}{\mathrm{2}}\:\mid\:{y}=\frac{\mathrm{5}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}} \\ $$$${x}=\frac{\mathrm{3}}{\mathrm{5}}.\frac{\mathrm{5}}{\mathrm{2}}\:\mid\:{x}=\frac{−\mathrm{3}}{\mathrm{5}}.\frac{\mathrm{5}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}} \\ $$$${x}=\frac{\mathrm{3}}{\mathrm{2}}\:\mid\:{x}=−\frac{\mathrm{3}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}} \\ $$$$\left(\frac{\mathrm{3}}{\mathrm{2}},\frac{\mathrm{5}}{\mathrm{2}}\right),\left(−\frac{\mathrm{3}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}},\frac{\mathrm{5}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}}\right) \\ $$
Answered by Rasheed.Sindhi last updated on 22/Aug/20
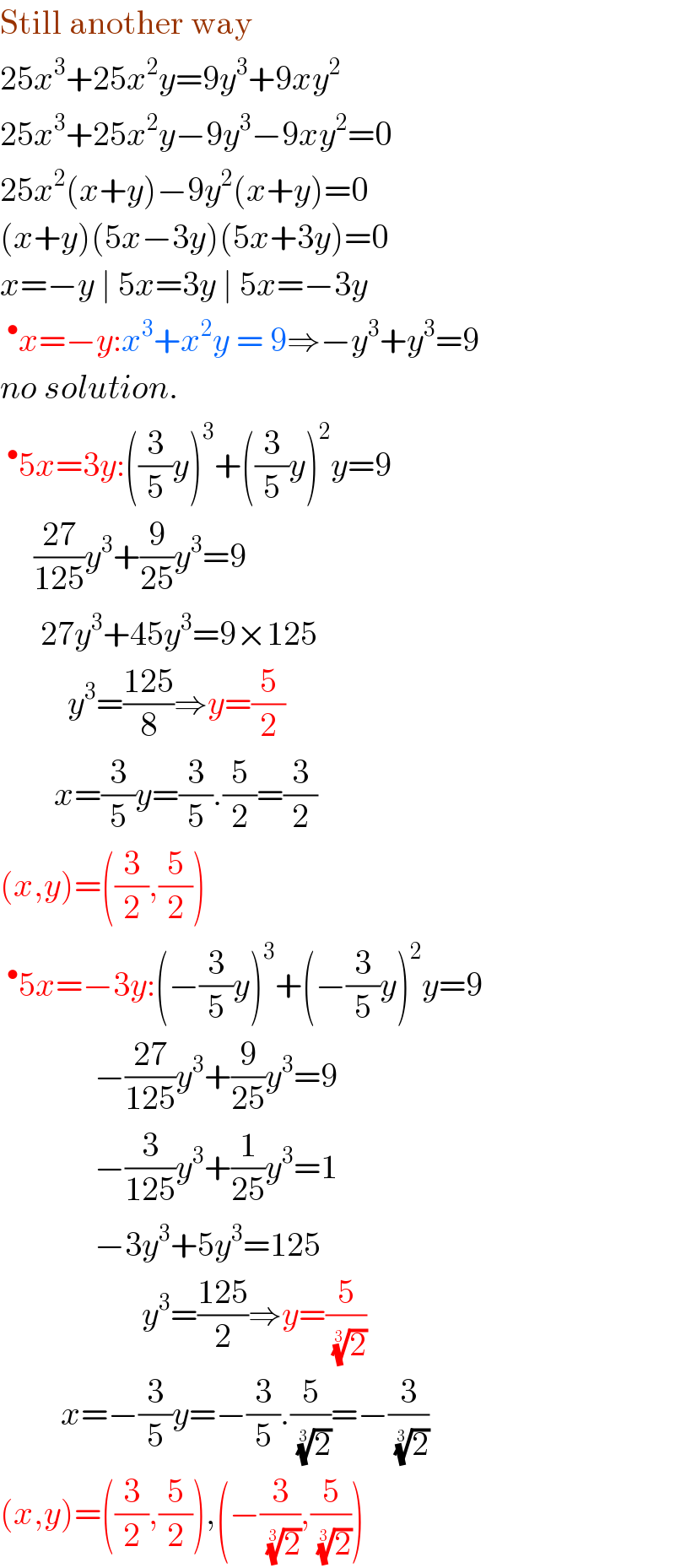
Still another way 25x^3 +25x^2 y=9y^3 +9xy^2 25x^3 +25x^2 y−9y^3 −9xy^2 =0 25x^2 (x+y)−9y^2 (x+y)=0 (x+y)(5x−3y)(5x+3y)=0 x=−y ∣ 5x=3y ∣ 5x=−3y ^• x=−y:x^3 +x^2 y = 9⇒−y^3 +y^3 =9 no solution. ^• 5x=3y:((3/5)y)^3 +((3/5)y)^2 y=9 ((27)/(125))y^3 +(9/(25))y^3 =9 27y^3 +45y^3 =9×125 y^3 =((125)/8)⇒y=(5/2) x=(3/5)y=(3/5).(5/2)=(3/2) (x,y)=((3/2),(5/2)) ^• 5x=−3y:(−(3/5)y)^3 +(−(3/5)y)^2 y=9 −((27)/(125))y^3 +(9/(25))y^3 =9 −(3/(125))y^3 +(1/(25))y^3 =1 −3y^3 +5y^3 =125 y^3 =((125)/2)⇒y=(5/( (2)^(1/3) )) x=−(3/5)y=−(3/5).(5/( (2)^(1/3) ))=−(3/( (2)^(1/3) )) (x,y)=((3/2),(5/2)),(−(3/( (2)^(1/3) )),(5/( (2)^(1/3) )))
$$\mathrm{Still}\:\mathrm{another}\:\mathrm{way} \\ $$$$\mathrm{25}{x}^{\mathrm{3}} +\mathrm{25}{x}^{\mathrm{2}} {y}=\mathrm{9}{y}^{\mathrm{3}} +\mathrm{9}{xy}^{\mathrm{2}} \\ $$$$\mathrm{25}{x}^{\mathrm{3}} +\mathrm{25}{x}^{\mathrm{2}} {y}−\mathrm{9}{y}^{\mathrm{3}} −\mathrm{9}{xy}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{25}{x}^{\mathrm{2}} \left({x}+{y}\right)−\mathrm{9}{y}^{\mathrm{2}} \left({x}+{y}\right)=\mathrm{0} \\ $$$$\left({x}+{y}\right)\left(\mathrm{5}{x}−\mathrm{3}{y}\right)\left(\mathrm{5}{x}+\mathrm{3}{y}\right)=\mathrm{0} \\ $$$${x}=−{y}\:\mid\:\mathrm{5}{x}=\mathrm{3}{y}\:\mid\:\mathrm{5}{x}=−\mathrm{3}{y} \\ $$$$\:^{\bullet} {x}=−{y}:{x}^{\mathrm{3}} +{x}^{\mathrm{2}} {y}\:=\:\mathrm{9}\Rightarrow−{y}^{\mathrm{3}} +{y}^{\mathrm{3}} =\mathrm{9} \\ $$$${no}\:{solution}. \\ $$$$\:^{\bullet} \mathrm{5}{x}=\mathrm{3}{y}:\left(\frac{\mathrm{3}}{\mathrm{5}}{y}\right)^{\mathrm{3}} +\left(\frac{\mathrm{3}}{\mathrm{5}}{y}\right)^{\mathrm{2}} {y}=\mathrm{9} \\ $$$$\:\:\:\:\:\frac{\mathrm{27}}{\mathrm{125}}{y}^{\mathrm{3}} +\frac{\mathrm{9}}{\mathrm{25}}{y}^{\mathrm{3}} =\mathrm{9} \\ $$$$\:\:\:\:\:\:\mathrm{27}{y}^{\mathrm{3}} +\mathrm{45}{y}^{\mathrm{3}} =\mathrm{9}×\mathrm{125} \\ $$$$\:\:\:\:\:\:\:\:\:\:{y}^{\mathrm{3}} =\frac{\mathrm{125}}{\mathrm{8}}\Rightarrow{y}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:{x}=\frac{\mathrm{3}}{\mathrm{5}}{y}=\frac{\mathrm{3}}{\mathrm{5}}.\frac{\mathrm{5}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\left({x},{y}\right)=\left(\frac{\mathrm{3}}{\mathrm{2}},\frac{\mathrm{5}}{\mathrm{2}}\right) \\ $$$$\:^{\bullet} \mathrm{5}{x}=−\mathrm{3}{y}:\left(−\frac{\mathrm{3}}{\mathrm{5}}{y}\right)^{\mathrm{3}} +\left(−\frac{\mathrm{3}}{\mathrm{5}}{y}\right)^{\mathrm{2}} {y}=\mathrm{9} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{27}}{\mathrm{125}}{y}^{\mathrm{3}} +\frac{\mathrm{9}}{\mathrm{25}}{y}^{\mathrm{3}} =\mathrm{9} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{3}}{\mathrm{125}}{y}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{25}}{y}^{\mathrm{3}} =\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{3}{y}^{\mathrm{3}} +\mathrm{5}{y}^{\mathrm{3}} =\mathrm{125} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{y}^{\mathrm{3}} =\frac{\mathrm{125}}{\mathrm{2}}\Rightarrow{y}=\frac{\mathrm{5}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\:\:{x}=−\frac{\mathrm{3}}{\mathrm{5}}{y}=−\frac{\mathrm{3}}{\mathrm{5}}.\frac{\mathrm{5}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}}=−\frac{\mathrm{3}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}} \\ $$$$\left({x},{y}\right)=\left(\frac{\mathrm{3}}{\mathrm{2}},\frac{\mathrm{5}}{\mathrm{2}}\right),\left(−\frac{\mathrm{3}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}},\frac{\mathrm{5}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}}\right) \\ $$
Answered by Her_Majesty last updated on 22/Aug/20
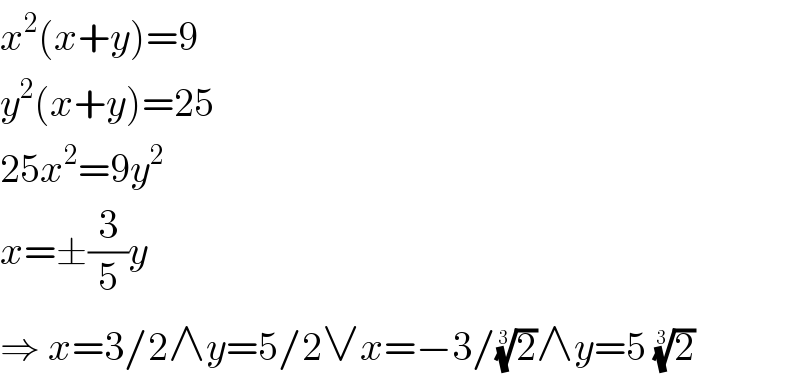
x^2 (x+y)=9 y^2 (x+y)=25 25x^2 =9y^2 x=±(3/5)y ⇒ x=3/2∧y=5/2∨x=−3/(2)^(1/3) ∧y=5 (2)^(1/3)
$${x}^{\mathrm{2}} \left({x}+{y}\right)=\mathrm{9} \\ $$$${y}^{\mathrm{2}} \left({x}+{y}\right)=\mathrm{25} \\ $$$$\mathrm{25}{x}^{\mathrm{2}} =\mathrm{9}{y}^{\mathrm{2}} \\ $$$${x}=\pm\frac{\mathrm{3}}{\mathrm{5}}{y} \\ $$$$\Rightarrow\:{x}=\mathrm{3}/\mathrm{2}\wedge{y}=\mathrm{5}/\mathrm{2}\vee{x}=−\mathrm{3}/\sqrt[{\mathrm{3}}]{\mathrm{2}}\wedge{y}=\mathrm{5}\:\sqrt[{\mathrm{3}}]{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *