Question Number 124252 by bramlexs22 last updated on 02/Dec/20
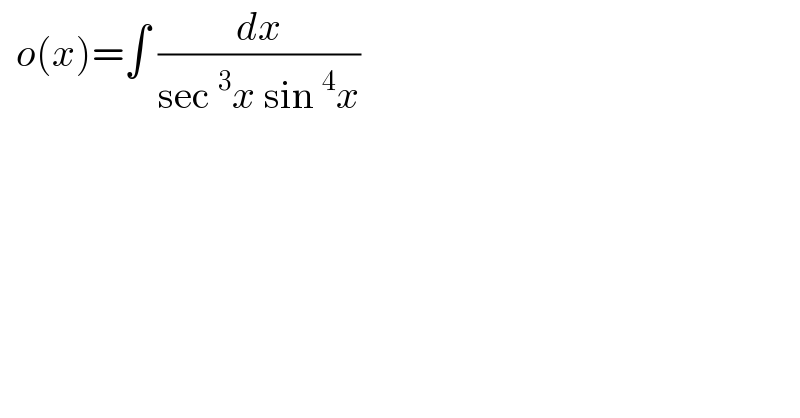
$$\:\:{o}\left({x}\right)=\int\:\frac{{dx}}{\mathrm{sec}\:^{\mathrm{3}} {x}\:\mathrm{sin}\:^{\mathrm{4}} {x}}\: \\ $$
Answered by Dwaipayan Shikari last updated on 02/Dec/20
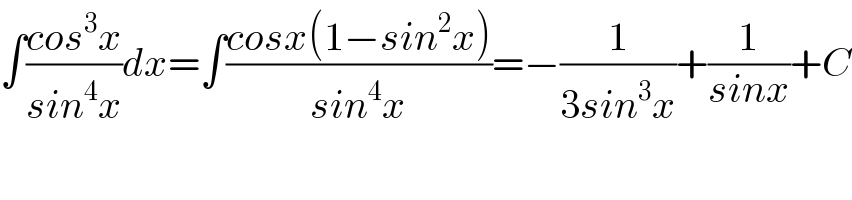
$$\int\frac{{cos}^{\mathrm{3}} {x}}{{sin}^{\mathrm{4}} {x}}{dx}=\int\frac{{cosx}\left(\mathrm{1}−{sin}^{\mathrm{2}} {x}\right)}{{sin}^{\mathrm{4}} {x}}=−\frac{\mathrm{1}}{\mathrm{3}{sin}^{\mathrm{3}} {x}}+\frac{\mathrm{1}}{{sinx}}+{C} \\ $$
