ODE-The-rate-at-which-the-ice-melt-is-proportional-to-the-amount-of-ice-present-at-the-instant-Find-the-amount-of-ice-left-after-2-hours-if-half-the-quantity-melt-in-30-minute-

Question Number 15800 by tawa tawa last updated on 14/Jun/17

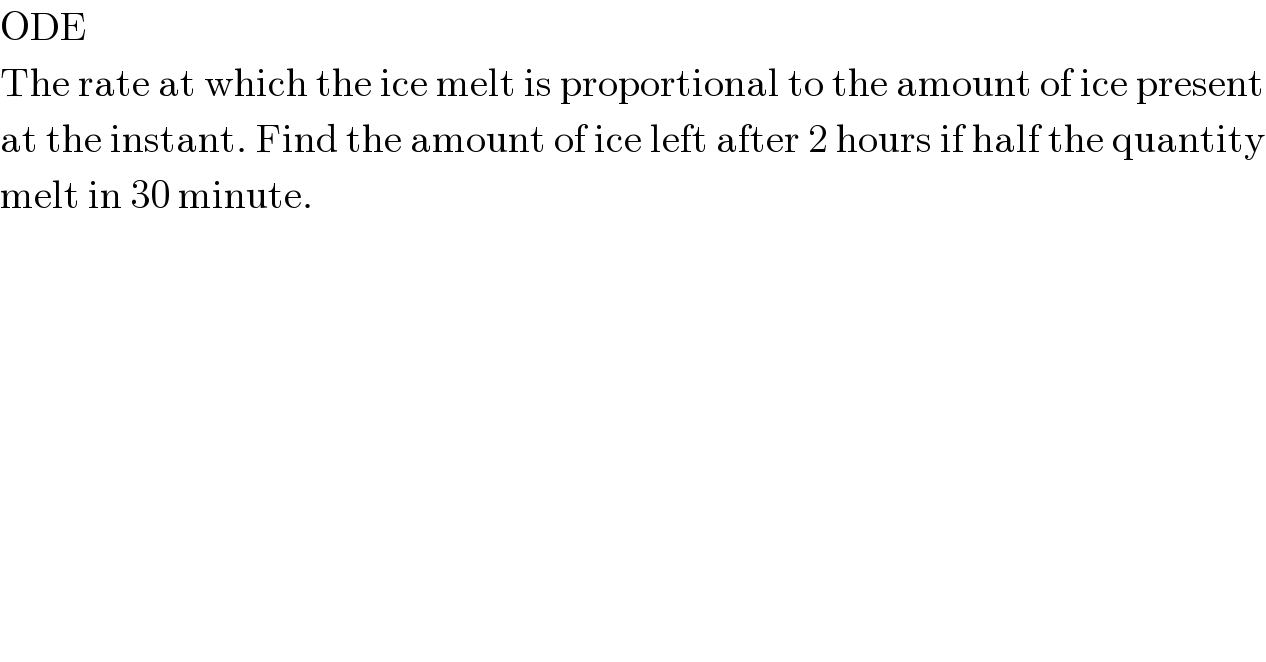
ODE

The rate at which the ice melt is proportional to the amount of ice present

at the instant . Find the amount of ice left after 2 hours if half the quantity

melt in 30 minute .

Answered by mrW1 last updated on 14/Jun/17

the ice melt in 0.5 hour by half of its amount, i . e

t = 0 . 5 h : \frac{1}{2} ice left

t = 1 h : \frac{1}{2} \times \frac{1}{2} ice left

t = 1 . 5 h : \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} ice left

t = 2 h : \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} ice left

\Rightarrow after 2 hours the amount of ice is \frac{1}{16}

general solution :

M = amout of ice

\frac{dM}{dt} = - kM with k = some constant

\frac{dM}{M} = - kdt

\ln M = - kt + C

M = e^{- kt + C} = M_{0} e^{- kt} with M_{0} = amout at t = 0

let m = \frac{M}{M_{0}}

\Rightarrow m = e^{- kt}

at t = t_{1} = 0 . 5 h : m_{1} = e^{- 0 . 5 k} = \frac{1}{2}

\Rightarrow e^{- 0 . 5 k} = \frac{1}{2}

at t = t_{2} = 2 h : m_{2} = e^{- 2 k} = {(e^{- 0 . 5 k})}^{4} = {(\frac{1}{2})}^{4} = \frac{1}{16}

further examples :

after t = 10 minutes

\frac{t}{t_{1}} = \frac{1}{3}

m = e^{- kt} = {(e^{- {kt}_{1}})}^{\frac{t}{t_{1}}} = {(\frac{1}{2})}^{\frac{1}{3}} = 0.79 (79 %)

after t = 45 minutes

\frac{t}{t_{1}} = 1.5

m = {(\frac{1}{2})}^{1.5} = 0.35 (35 %)

Commented by tawa tawa last updated on 14/Jun/17

God bless you sir . i really appreciate .