Question Number 29359 by NECx last updated on 08/Feb/18

$${On}\:{a}\:{two}\:{lane}\:{road},{car}\:{A}\:{is} \\ $$$${travelling}\:{with}\:{a}\:{speed}\:{of}\:\mathrm{36}{km}/{h}. \\ $$$${Two}\:{cars}\:{B}\:{and}\:{C}\:{approach}\:{A}\:{in} \\ $$$${opposite}\:{directions}\:{with}\:{a}\:{speed}\:{of} \\ $$$$\mathrm{54}{km}/{h}\:{each}.{At}\:{a}\:{certain}\:{instant}, \\ $$$${when}\:{the}\:{distance}\:{AB}\:{is}\:{equal} \\ $$$${to}\:{AC},{both}\:{being}\:\mathrm{1}{km},{B}\:{decides} \\ $$$${to}\:{overtake}\:{A}\:{before}\:{C}\:{does}.{What} \\ $$$${minimum}\:{acceleration}\:{of}\:{carB} \\ $$$${is}\:{required}\:{to}\:{avoid}\:{an}\:{accident}? \\ $$
Answered by 33 last updated on 08/Feb/18
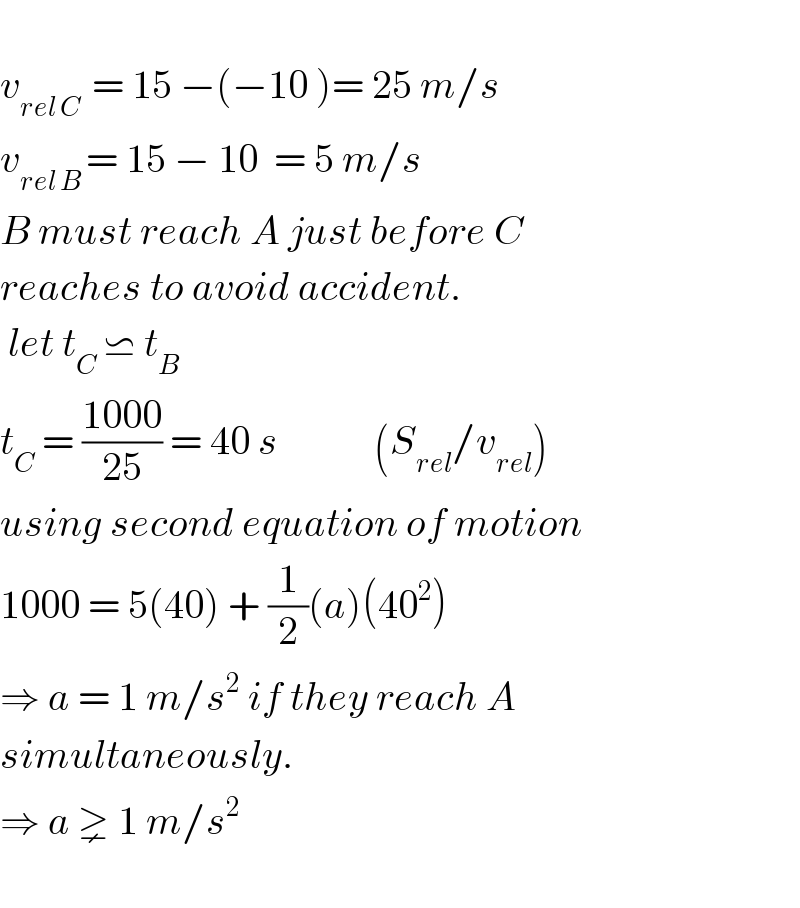
$$ \\ $$$${v}_{{rel}\:{C}\:} \:=\:\mathrm{15}\:−\left(−\mathrm{10}\:\right)=\:\mathrm{25}\:{m}/{s} \\ $$$${v}_{{rel}\:{B}\:} =\:\mathrm{15}\:−\:\mathrm{10}\:\:=\:\mathrm{5}\:{m}/{s} \\ $$$${B}\:{must}\:{reach}\:{A}\:{just}\:{before}\:{C} \\ $$$${reaches}\:{to}\:{avoid}\:{accident}. \\ $$$$\:{let}\:{t}_{{C}} \:\backsimeq\:{t}_{{B}} \\ $$$${t}_{{C}} \:=\:\frac{\mathrm{1000}}{\mathrm{25}}\:=\:\mathrm{40}\:{s}\:\:\:\:\:\:\:\:\:\:\:\:\left({S}_{{rel}} /{v}_{{rel}} \right) \\ $$$${using}\:{second}\:{equation}\:{of}\:{motion} \\ $$$$\mathrm{1000}\:=\:\mathrm{5}\left(\mathrm{40}\right)\:+\:\frac{\mathrm{1}}{\mathrm{2}}\left({a}\right)\left(\mathrm{40}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:{a}\:=\:\mathrm{1}\:{m}/{s}^{\mathrm{2}} \:{if}\:{they}\:{reach}\:{A} \\ $$$${simultaneously}. \\ $$$$\Rightarrow\:{a}\:\gneq\:\mathrm{1}\:{m}/{s}^{\mathrm{2}} \\ $$$$ \\ $$
