Question Number 145134 by ArielVyny last updated on 02/Jul/21

$${On}\:{dispose}\:{de}\:{N}+\mathrm{1}\:{urnes}.{l}'{urne}\:{U}_{{k}} \\ $$$${contient}\:{k}\:{boules}\:{blanches}\:{et}\:{N}−{k}\:{boules} \\ $$$${noires}.{on}\:{tire}\:{successivement}\:{sans}\: \\ $$$${remise}\:{n}\:{boules}\:{de}\:{l}'{urne}\:{et}\:{on}\:{note}\: \\ $$$${An}\:{l}'{evenement}\:''{choisir}\:{n}\:{boules}\:{noires} \\ $$$${lors}\:{des}\:{n}\:{premiers}\:{tirages}''.\:{Determiner} \\ $$$${P}\left({An}\right).\:{on}\:{notera}\:{U}_{{k}} =''{choisir}\:{l}'{urne}\:{k}'' \\ $$
Commented by Olaf_Thorendsen last updated on 03/Jul/21
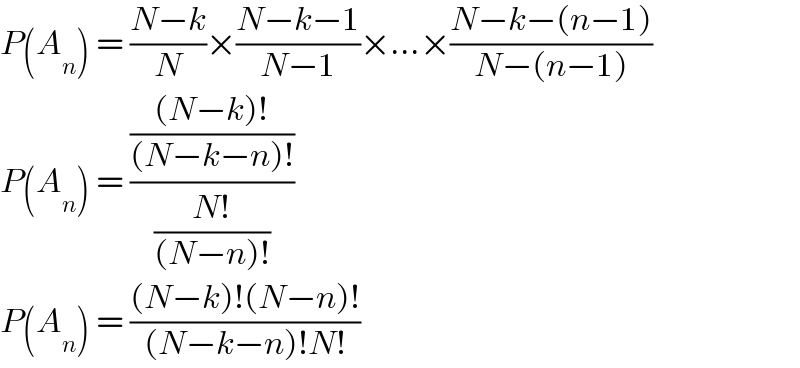
$${P}\left({A}_{{n}} \right)\:=\:\frac{{N}−{k}}{{N}}×\frac{{N}−{k}−\mathrm{1}}{{N}−\mathrm{1}}×…×\frac{{N}−{k}−\left({n}−\mathrm{1}\right)}{{N}−\left({n}−\mathrm{1}\right)} \\ $$$${P}\left({A}_{{n}} \right)\:=\:\frac{\frac{\left({N}−{k}\right)!}{\left({N}−{k}−{n}\right)!}}{\frac{{N}!}{\left({N}−{n}\right)!}} \\ $$$${P}\left({A}_{{n}} \right)\:=\:\frac{\left({N}−{k}\right)!\left({N}−{n}\right)!}{\left({N}−{k}−{n}\right)!{N}!} \\ $$
