Question Number 147381 by puissant last updated on 20/Jul/21
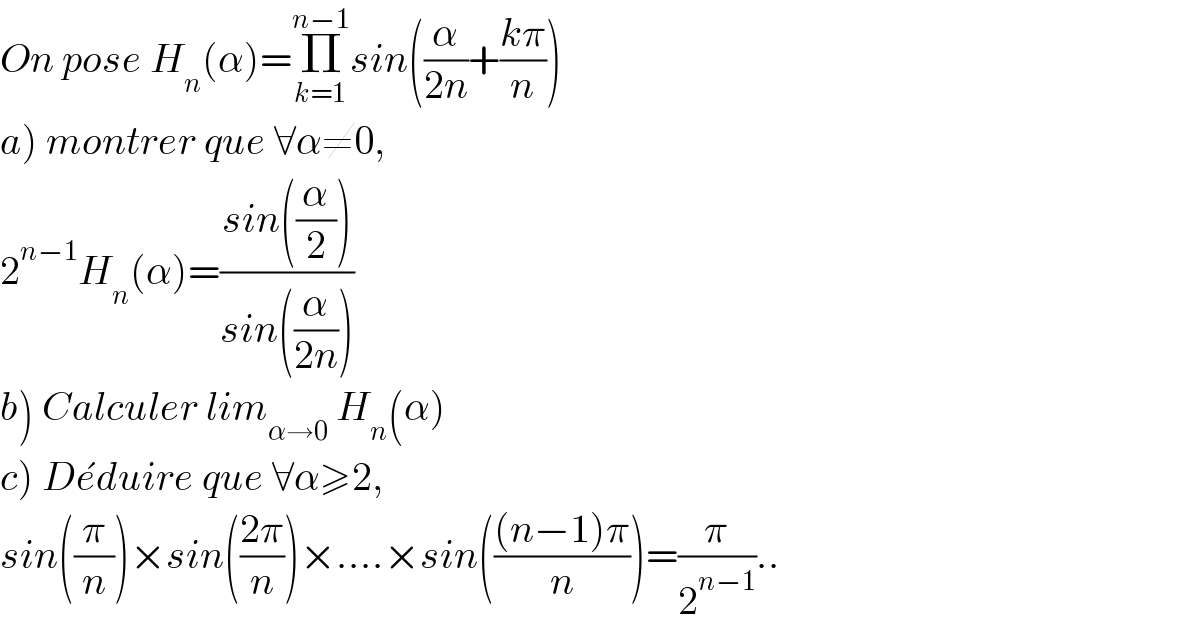
$${On}\:{pose}\:{H}_{{n}} \left(\alpha\right)=\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\prod}}{sin}\left(\frac{\alpha}{\mathrm{2}{n}}+\frac{{k}\pi}{{n}}\right) \\ $$$$\left.{a}\right)\:{montrer}\:{que}\:\forall\alpha\neq\mathrm{0},\: \\ $$$$\mathrm{2}^{{n}−\mathrm{1}} {H}_{{n}} \left(\alpha\right)=\frac{{sin}\left(\frac{\alpha}{\mathrm{2}}\right)}{{sin}\left(\frac{\alpha}{\mathrm{2}{n}}\right)} \\ $$$$\left.{b}\right)\:{Calculer}\:{lim}_{\alpha\rightarrow\mathrm{0}} \:{H}_{{n}} \left(\alpha\right) \\ $$$$\left.{c}\right)\:{D}\acute {{e}duire}\:{que}\:\forall\alpha\geqslant\mathrm{2},\: \\ $$$${sin}\left(\frac{\pi}{{n}}\right)×{sin}\left(\frac{\mathrm{2}\pi}{{n}}\right)×….×{sin}\left(\frac{\left({n}−\mathrm{1}\right)\pi}{{n}}\right)=\frac{\pi}{\mathrm{2}^{{n}−\mathrm{1}} }.. \\ $$
Answered by Olaf_Thorendsen last updated on 20/Jul/21

$$\left.{a}\right) \\ $$$$\mathrm{P}\left({z}\right)\:=\:{z}^{{n}} −{e}^{{i}\alpha} \\ $$$$\mathrm{P}\left({z}_{{k}} \right)\:=\:\mathrm{0}\:\Leftrightarrow\:{z}_{{k}} \:=\:{e}^{{i}\left(\frac{\alpha}{{n}}+\frac{\mathrm{2}{k}\pi}{{n}}\right)} ,\:{k}\:=\:\mathrm{0},\:\mathrm{1}…,\:{n}−\mathrm{1} \\ $$$$\mathrm{P}\left({z}\right)\:=\:\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left({z}−{z}_{{k}} \right) \\ $$$$\mathrm{P}\left({z}\right)\:=\:\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left({z}−{e}^{{i}\left(\frac{\alpha}{{n}}+\frac{\mathrm{2}{k}\pi}{{n}}\right)} \right) \\ $$$$\mathrm{P}\left(\mathrm{1}\right)\:=\:\mathrm{1}−{e}^{{i}\alpha} \:=\:\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left(\mathrm{1}−{e}^{{i}\left(\frac{\alpha}{{n}}+\frac{\mathrm{2}{k}\pi}{{n}}\right)} \right) \\ $$$$\mathrm{1}−{e}^{{i}\alpha} \:=\:\left(\mathrm{1}−{e}^{{i}\frac{\alpha}{{n}}} \right)\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\prod}}\left(\mathrm{1}−{e}^{{i}\left(\frac{\alpha}{{n}}+\frac{\mathrm{2}{k}\pi}{{n}}\right)} \right) \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\prod}}\left(\mathrm{1}−{e}^{{i}\left(\frac{\alpha}{{n}}+\frac{\mathrm{2}{k}\pi}{{n}}\right)} \right)\:=\:\frac{\mathrm{1}−{e}^{{i}\alpha} }{\mathrm{1}−{e}^{{i}\frac{\alpha}{{n}}} } \\ $$$$\mathrm{C}'\mathrm{est}\:\mathrm{fastidieux}\:\mathrm{mais}\:\mathrm{il}\:\mathrm{suffit}\:\mathrm{de} \\ $$$$\mathrm{factoriser}\:\mathrm{partout}\:\mathrm{par}\:\mathrm{l}'\mathrm{exponentielle} \\ $$$$\mathrm{de}\:\mathrm{la}\:\mathrm{demi}\:\mathrm{somme}\:\mathrm{pour}\:\mathrm{voir}\:\mathrm{apparaitre} \\ $$$$\mathrm{le}\:\mathrm{resultat}. \\ $$$$\mathrm{Par}\:\mathrm{exemple}\:\mathrm{1}−{e}^{{i}\alpha} \:\mathrm{est}\:\mathrm{factorise}\:\mathrm{en} \\ $$$${e}^{{i}\frac{\alpha}{\mathrm{2}}} \left({e}^{−{i}\frac{\alpha}{\mathrm{2}}} −{e}^{{i}\frac{\alpha}{\mathrm{2}}} \right)…\:{etc}… \\ $$$$ \\ $$
