Question Number 144738 by Ar Brandon last updated on 28/Jun/21

$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{On}\:\mathrm{souhaite}\:\mathrm{calculer}\:\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}{t}}{{t}}{dt}. \\ $$$$\left(\mathrm{1}\right)\:\mathrm{On}\:\mathrm{d}\acute {\mathrm{e}finit}\:\mathrm{la}\:\mathrm{fonction}\:{F}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} {e}^{−{tx}} \frac{\mathrm{sin}{t}}{{t}}{dt}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{a}\right)\:\mathrm{D}\acute {\mathrm{e}terminer}\:\mathrm{le}\:\mathrm{domaine}\:\mathrm{de}\:\mathrm{d}\acute {\mathrm{e}finition}\:\mathrm{de}\:{f}\:\mathrm{sur}\:\mathbb{R}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{b}\right)\:\mathrm{Montrer}\:\mathrm{que}\:{F}\:\mathrm{est}\:\mathrm{de}\:\mathrm{classe}\:{C}^{\mathrm{1}} \:\mathrm{sur}\:{R}_{+} ^{\ast} \:\mathrm{et}\:\mathrm{calculer}\:{F}\:'\left({x}\right). \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{c}\right)\:\mathrm{Limite}\:\mathrm{de}\:{F}\:\mathrm{en}\:+\infty\:?\:\mathrm{Cons}\acute {\mathrm{e}quence}\:? \\ $$$$\left(\mathrm{2}\right)\:\mathrm{On}\:\mathrm{note}\:{Si}\left({t}\right)=\int_{\mathrm{0}} ^{{t}} \frac{\mathrm{sin}{u}}{{u}}{du}\:\mathrm{pour}\:\mathrm{tout}\:\mathrm{r}\acute {\mathrm{e}el}\:{t}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{a}\right)\:\mathrm{Montrer}\:\mathrm{que}\:{G}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} {e}^{−{tx}} {Si}\left({t}\right){dt}\:\mathrm{est}\:\mathrm{d}\acute {\mathrm{e}finie}\:\mathrm{sur}\:{R}_{+} ^{\ast} . \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{b}\right)\:\mathrm{Montrer}\:\mathrm{que}\:{xG}\left({x}\right)\rightarrow{I}\:\mathrm{quand}\:{x}\rightarrow\mathrm{0}^{+} . \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{c}\right)\:\mathrm{Au}\:\mathrm{moyen}\:\mathrm{d}'\mathrm{une}\:\mathrm{int}\acute {\mathrm{e}gration}\:\mathrm{par}\:\mathrm{parties},\:\mathrm{montrer}\:\mathrm{que}\:{F}\:\mathrm{est}\:\mathrm{continue}\:\mathrm{en}\:\mathrm{0}. \\ $$$$\left(\mathrm{3}\right)\:\mathrm{Calculer}\:{I}. \\ $$
Answered by Dwaipayan Shikari last updated on 28/Jun/21
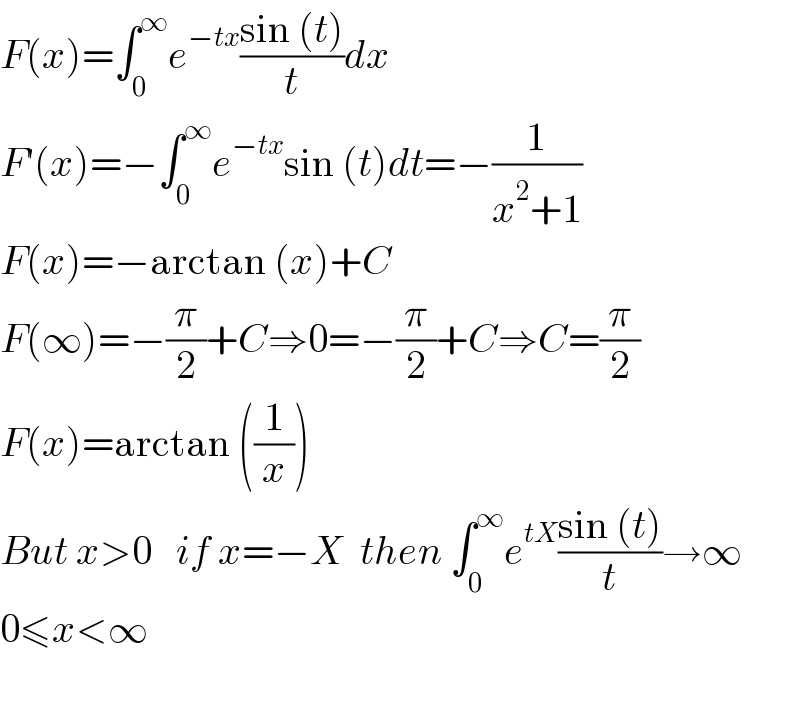
$${F}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} {e}^{−{tx}} \frac{\mathrm{sin}\:\left({t}\right)}{{t}}{dx} \\ $$$${F}'\left({x}\right)=−\int_{\mathrm{0}} ^{\infty} {e}^{−{tx}} \mathrm{sin}\:\left({t}\right){dt}=−\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${F}\left({x}\right)=−\mathrm{arctan}\:\left({x}\right)+{C} \\ $$$${F}\left(\infty\right)=−\frac{\pi}{\mathrm{2}}+{C}\Rightarrow\mathrm{0}=−\frac{\pi}{\mathrm{2}}+{C}\Rightarrow{C}=\frac{\pi}{\mathrm{2}} \\ $$$${F}\left({x}\right)=\mathrm{arctan}\:\left(\frac{\mathrm{1}}{{x}}\right) \\ $$$${But}\:{x}>\mathrm{0}\:\:\:{if}\:{x}=−{X}\:\:{then}\:\int_{\mathrm{0}} ^{\infty} {e}^{{tX}} \frac{\mathrm{sin}\:\left({t}\right)}{{t}}\rightarrow\infty \\ $$$$\mathrm{0}\leqslant{x}<\infty \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 02/Aug/21

$$\mathrm{Hello}\:\mathrm{bro}\:!!! \\ $$$$ \\ $$
