Menu Close

on-the-interval-of-0-pi-solve-tan-2-x-3secx-3-

Tinku Tara 0 Comments
Pin




Question Number 107978 by anonymous last updated on 13/Aug/20
on the interval of [0,π] solve tan^2 x+3secx= −3
ontheintervalof[0,π]solvetan2x+3secx=−3
Answered by bemath last updated on 14/Aug/20
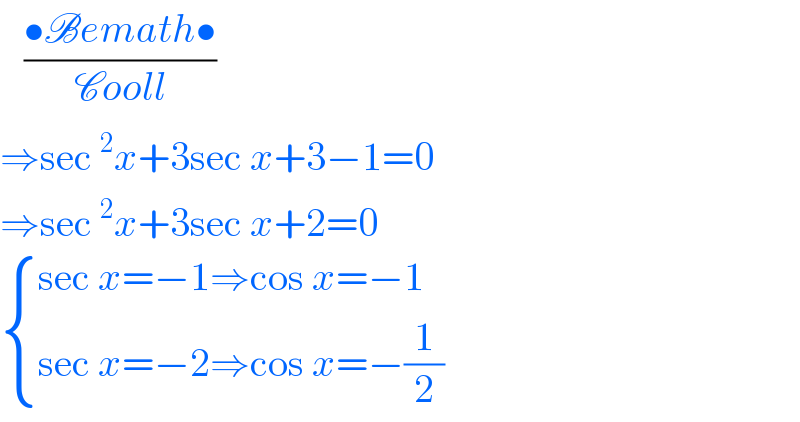
((•Bemath•)/(Cooll)) ⇒sec^2 x+3sec x+3−1=0 ⇒sec^2 x+3sec x+2=0 { ((sec x=−1⇒cos x=−1)),((sec x=−2⇒cos x=−(1/2))) :}
∙Bemath∙Cooll⇒sec2x+3secx+3−1=0⇒sec2x+3secx+2=0{secx=−1⇒cosx=−1secx=−2⇒cosx=−12
Commented by anonymous last updated on 13/Aug/20
Thank alot sif
Thankalotsif
Commented by aleks041103 last updated on 13/Aug/20
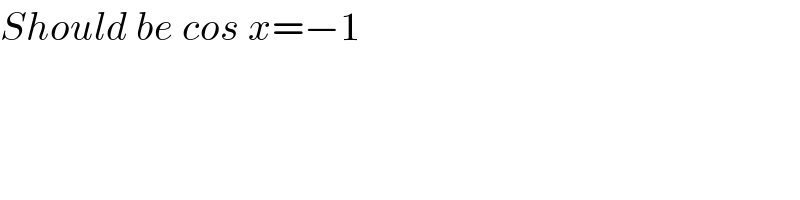
Should be cos x=−1
Shouldbecosx=−1
Commented by bemath last updated on 14/Aug/20
yes....cooll
yes….cooll

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *