ordinary-differential-equation-y-xy-y-0-general-solution-m-n-1970-

Question Number 118364 by mnjuly1970 last updated on 17/Oct/20

\dots o r d i n a r y d i f f e r e n t i a l e q u a t i o n \dots

y^{″} - {x y}^{'} + y = 0

g e n e r a l s o l u t i o n ::= ? ?

. m . n . 1970 .

Answered by mindispower last updated on 17/Oct/20

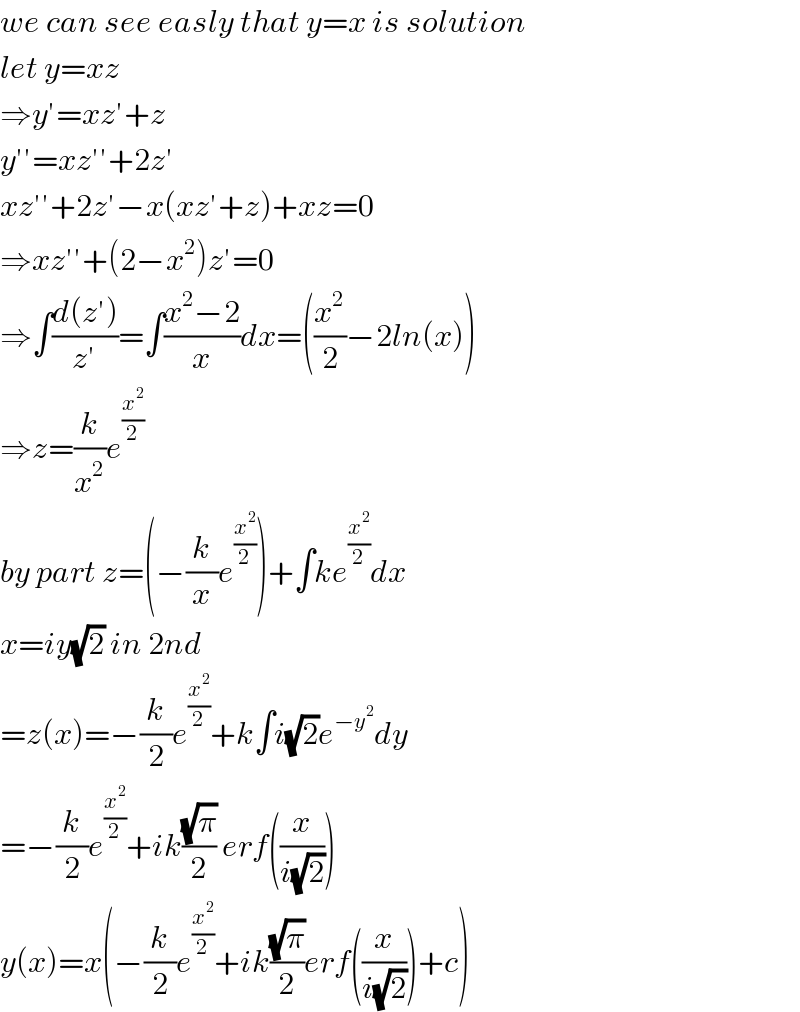
w e c a n s e e e a s l y t h a t y = x i s s o l u t i o n

l e t y = x z

\Rightarrow y^{'} = {x z}^{'} + z

y^{″} = {x z}^{″} + 2 z^{'}

{x z}^{″} + 2 z^{'} - x ({x z}^{'} + z) + x z = 0

\Rightarrow {x z}^{″} + (2 - x^{2}) z^{'} = 0

\Rightarrow \int \frac{d (z^{'})}{z^{'}} = \int \frac{x^{2} - 2}{x} d x = (\frac{x^{2}}{2} - 2 l n (x))

\Rightarrow z = \frac{k}{x^{2}} e^{\frac{x^{2}}{2}}

b y p a r t z = (- \frac{k}{x} e^{\frac{x^{2}}{2}}) + \int {k e}^{\frac{x^{2}}{2}} d x

x = i y \sqrt{2} i n 2 n d

= z (x) = - \frac{k}{2} e^{\frac{x^{2}}{2}} + k \int i \sqrt{2} e^{- y^{2}} d y

= - \frac{k}{2} e^{\frac{x^{2}}{2}} + i k \frac{\sqrt{π}}{2} e r f (\frac{x}{i \sqrt{2}})

y (x) = x (- \frac{k}{2} e^{\frac{x^{2}}{2}} + i k \frac{\sqrt{π}}{2} e r f (\frac{x}{i \sqrt{2}}) + c)

Commented by mnjuly1970 last updated on 17/Oct/20

t h a n k y o u s o m u c h m r \dots

Commented by mindispower last updated on 19/Oct/20

w i t h e p l e a s u r s i r