Question Number 91277 by john santu last updated on 29/Apr/20
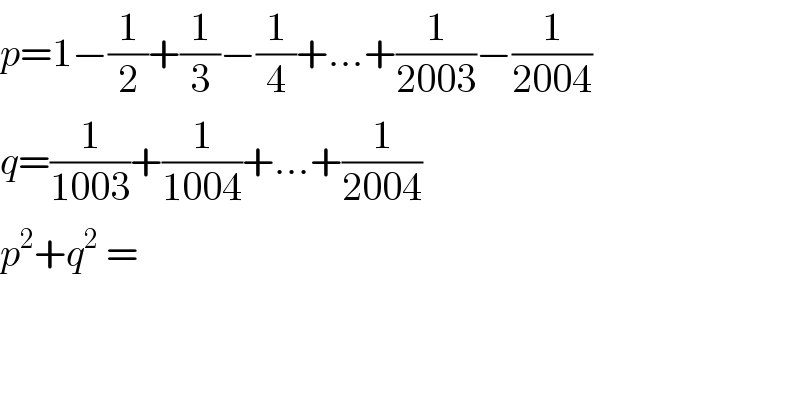
$${p}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}+…+\frac{\mathrm{1}}{\mathrm{2003}}−\frac{\mathrm{1}}{\mathrm{2004}} \\ $$$${q}=\frac{\mathrm{1}}{\mathrm{1003}}+\frac{\mathrm{1}}{\mathrm{1004}}+…+\frac{\mathrm{1}}{\mathrm{2004}} \\ $$$${p}^{\mathrm{2}} +{q}^{\mathrm{2}} \:=\: \\ $$
Answered by naka3546 last updated on 30/Apr/20

Commented by jagoll last updated on 30/Apr/20
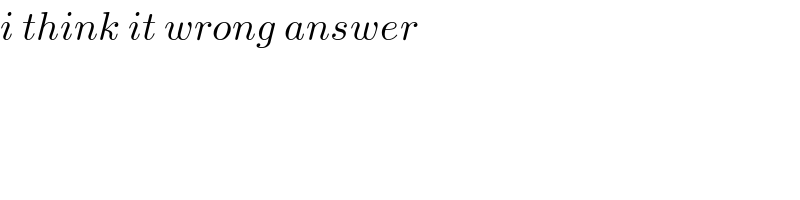
$${i}\:{think}\:{it}\:{wrong}\:{answer} \\ $$
Commented by naka3546 last updated on 30/Apr/20
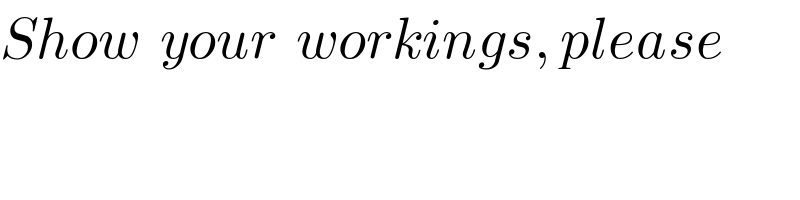
$${Show}\:\:{your}\:\:{workings},\:{please}\: \\ $$
Answered by naka3546 last updated on 30/Apr/20

