Question Number 105239 by bemath last updated on 27/Jul/20
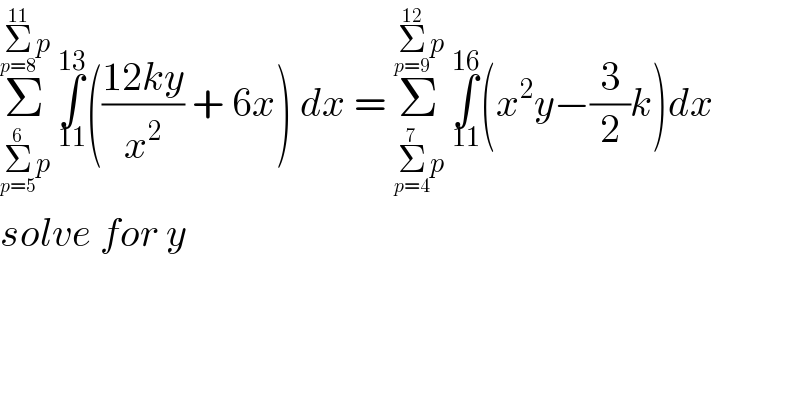
$$\underset{\underset{{p}=\mathrm{5}} {\overset{\mathrm{6}} {\sum}}{p}} {\overset{\underset{{p}=\mathrm{8}} {\overset{\mathrm{11}} {\sum}}{p}} {\sum}}\:\underset{\mathrm{11}} {\overset{\mathrm{13}} {\int}}\left(\frac{\mathrm{12}{ky}}{{x}^{\mathrm{2}} }\:+\:\mathrm{6}{x}\right)\:{dx}\:=\:\underset{\underset{{p}=\mathrm{4}} {\overset{\mathrm{7}} {\sum}}{p}} {\overset{\underset{{p}=\mathrm{9}} {\overset{\mathrm{12}} {\sum}}{p}} {\sum}}\:\underset{\mathrm{11}} {\overset{\mathrm{16}} {\int}}\left({x}^{\mathrm{2}} {y}−\frac{\mathrm{3}}{\mathrm{2}}{k}\right){dx} \\ $$$${solve}\:{for}\:{y} \\ $$
Answered by john santu last updated on 27/Jul/20
![(1)Σ_(p = 5) ^6 p = 11 (2) Σ_(p = 8) ^(11) p = 38 (3) Σ_(p = 4) ^7 p = 22 (4) Σ_(p = 9) ^(12) p = 42 ⇔ Σ_(11) ^(38) ∫_(11) ^(13) (12kx^(−2) y +6x) dx= Σ_(11) ^(38) [(−((12ky)/x)+3x^2 )]_(11) ^(13) =Σ_(11) ^(38) (3(48)+12ky((1/(11))−(1/(13)))) the strange question .](https://www.tinkutara.com/question/Q105241.png)
$$\left(\mathrm{1}\right)\underset{{p}\:=\:\mathrm{5}} {\overset{\mathrm{6}} {\sum}}{p}\:=\:\mathrm{11} \\ $$$$\left(\mathrm{2}\right)\:\underset{{p}\:=\:\mathrm{8}} {\overset{\mathrm{11}} {\sum}}{p}\:=\:\mathrm{38}\: \\ $$$$\left(\mathrm{3}\right)\:\underset{{p}\:=\:\mathrm{4}} {\overset{\mathrm{7}} {\sum}}{p}\:=\:\mathrm{22} \\ $$$$\left(\mathrm{4}\right)\:\underset{{p}\:=\:\mathrm{9}} {\overset{\mathrm{12}} {\sum}}{p}\:=\:\mathrm{42} \\ $$$$\Leftrightarrow\:\underset{\mathrm{11}} {\overset{\mathrm{38}} {\sum}}\:\underset{\mathrm{11}} {\overset{\mathrm{13}} {\int}}\left(\mathrm{12}{kx}^{−\mathrm{2}} {y}\:+\mathrm{6}{x}\right)\:{dx}= \\ $$$$\underset{\mathrm{11}} {\overset{\mathrm{38}} {\sum}}\:\left[\left(−\frac{\mathrm{12}{ky}}{{x}}+\mathrm{3}{x}^{\mathrm{2}} \right)\right]_{\mathrm{11}} ^{\mathrm{13}} =\underset{\mathrm{11}} {\overset{\mathrm{38}} {\sum}}\left(\mathrm{3}\left(\mathrm{48}\right)+\mathrm{12}{ky}\left(\frac{\mathrm{1}}{\mathrm{11}}−\frac{\mathrm{1}}{\mathrm{13}}\right)\right) \\ $$$${the}\:{strange}\:{question}\:. \\ $$
