Question Number 147302 by puissant last updated on 19/Jul/21
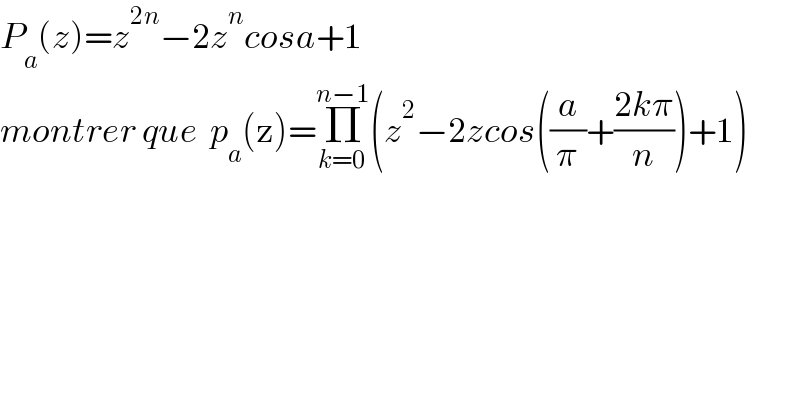
$${P}_{{a}} \left({z}\right)={z}^{\mathrm{2}{n}} −\mathrm{2}{z}^{{n}} {cosa}+\mathrm{1} \\ $$$${montrer}\:{que}\:\:{p}_{{a}} \left(\mathrm{z}\right)=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left({z}^{\mathrm{2}} −\mathrm{2}{zcos}\left(\frac{{a}}{\pi}+\frac{\mathrm{2}{k}\pi}{{n}}\right)+\mathrm{1}\right) \\ $$
Answered by mathmax by abdo last updated on 20/Jul/21
![p_a (z)=z^(2n) −2z^n cosa +1 let z^n =x ⇒ p_a (z)=x^2 −2(cosa)x+1 Δ^′ =cos^2 a−1=−sin^2 a ⇒x_1 =cosa +isina =e^(ia) and x_2 =e^(−ia) ⇒p_a (z)=(z^n −e^(ia) )(z^n −e^(−ia) ) z^n =e^(ia) for z=e^(iθ) ⇒niθ=i(a+2kπ) ⇒θ_k =((a+2kπ)/(2n)) k∈[[0,n−1]] ⇒z_k =e^(i(((a+2kπ)/n))) the roots of z^n −e^(ia) =0 are α_k =e^(−i(((a+2kπ)/n))) ⇒ p_a (z)=Π_(k=0) ^(n−1) (z−e^(i(((a+2kπ)/n))) )(z−e^(−i(((a+2kπ)/n))) ) =Π_(k=0) ^(n−1) (z−z_k )(z−z_k ^− )=Π_(k=0) ^(n−1) (z^2 −2Re(z_k )z +∣z_k ∣^2 ) =Π_(k=0) ^(n−1) (z^2 −2cos((a/n)+((2kπ)/n))z+1)](https://www.tinkutara.com/question/Q147347.png)
$$\mathrm{p}_{\mathrm{a}} \left(\mathrm{z}\right)=\mathrm{z}^{\mathrm{2n}} −\mathrm{2z}^{\mathrm{n}} \mathrm{cosa}\:+\mathrm{1}\:\:\mathrm{let}\:\mathrm{z}^{\mathrm{n}} \:=\mathrm{x}\:\Rightarrow \\ $$$$\mathrm{p}_{\mathrm{a}} \left(\mathrm{z}\right)=\mathrm{x}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{cosa}\right)\mathrm{x}+\mathrm{1} \\ $$$$\Delta^{'} \:=\mathrm{cos}^{\mathrm{2}} \mathrm{a}−\mathrm{1}=−\mathrm{sin}^{\mathrm{2}} \mathrm{a}\:\Rightarrow\mathrm{x}_{\mathrm{1}} =\mathrm{cosa}\:+\mathrm{isina}\:=\mathrm{e}^{\mathrm{ia}} \:\mathrm{and}\:\mathrm{x}_{\mathrm{2}} =\mathrm{e}^{−\mathrm{ia}} \\ $$$$\Rightarrow\mathrm{p}_{\mathrm{a}} \left(\mathrm{z}\right)=\left(\mathrm{z}^{\mathrm{n}} −\mathrm{e}^{\mathrm{ia}} \right)\left(\mathrm{z}^{\mathrm{n}} −\mathrm{e}^{−\mathrm{ia}} \right) \\ $$$$\mathrm{z}^{\mathrm{n}} \:=\mathrm{e}^{\mathrm{ia}} \:\:\mathrm{for}\:\mathrm{z}=\mathrm{e}^{\mathrm{i}\theta} \:\Rightarrow\mathrm{ni}\theta=\mathrm{i}\left(\mathrm{a}+\mathrm{2k}\pi\right)\:\Rightarrow\theta_{\mathrm{k}} =\frac{\mathrm{a}+\mathrm{2k}\pi}{\mathrm{2n}}\:\:\:\:\mathrm{k}\in\left[\left[\mathrm{0},\mathrm{n}−\mathrm{1}\right]\right] \\ $$$$\Rightarrow\mathrm{z}_{\mathrm{k}} =\mathrm{e}^{\mathrm{i}\left(\frac{\mathrm{a}+\mathrm{2k}\pi}{\mathrm{n}}\right)} \:\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{z}^{\mathrm{n}} −\mathrm{e}^{\mathrm{ia}} \:=\mathrm{0}\:\mathrm{are}\:\alpha_{\mathrm{k}} =\mathrm{e}^{−\mathrm{i}\left(\frac{\mathrm{a}+\mathrm{2k}\pi}{\mathrm{n}}\right)} \:\Rightarrow \\ $$$$\mathrm{p}_{\mathrm{a}} \left(\mathrm{z}\right)=\prod_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \left(\mathrm{z}−\mathrm{e}^{\mathrm{i}\left(\frac{\mathrm{a}+\mathrm{2k}\pi}{\mathrm{n}}\right)} \right)\left(\mathrm{z}−\mathrm{e}^{−\mathrm{i}\left(\frac{\mathrm{a}+\mathrm{2k}\pi}{\mathrm{n}}\right)} \right) \\ $$$$=\prod_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \left(\mathrm{z}−\mathrm{z}_{\mathrm{k}} \right)\left(\mathrm{z}−\overset{−} {\mathrm{z}}_{\mathrm{k}} \right)=\prod_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \left(\mathrm{z}^{\mathrm{2}} −\mathrm{2Re}\left(\mathrm{z}_{\mathrm{k}} \right)\mathrm{z}\:+\mid\mathrm{z}_{\mathrm{k}} \mid^{\mathrm{2}} \right) \\ $$$$=\prod_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \left(\mathrm{z}^{\mathrm{2}} \:−\mathrm{2cos}\left(\frac{\mathrm{a}}{\mathrm{n}}+\frac{\mathrm{2k}\pi}{\mathrm{n}}\right)\mathrm{z}+\mathrm{1}\right) \\ $$
Commented by puissant last updated on 20/Jul/21

$$\mathrm{thanks}\:\mathrm{sir} \\ $$
