Menu Close

P-cos-pi-15-cos-2pi-15-cos-3pi-15-cos-4pi-15-cos-5pi-15-cos-6pi-15-cos-7pi-15-

Tinku Tara 0 Comments
Pin




Question Number 130469 by liberty last updated on 26/Jan/21
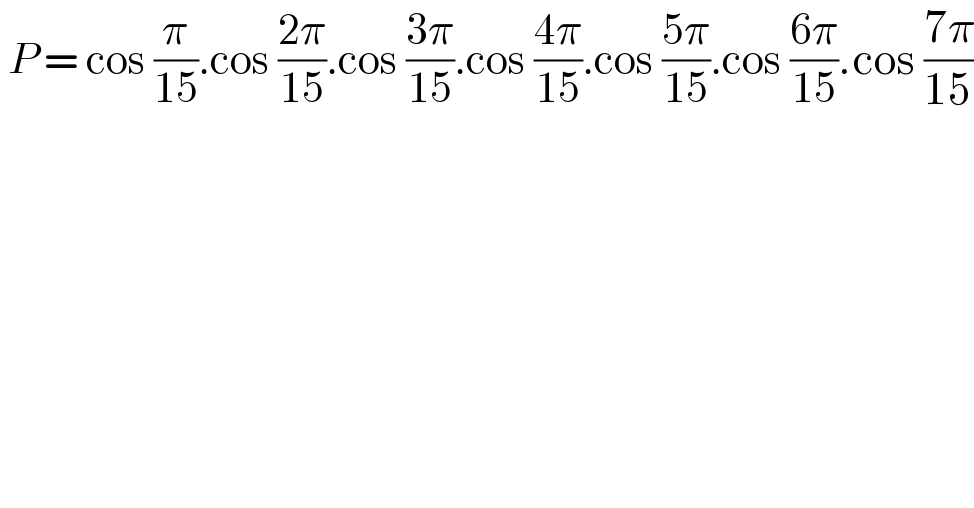
P = cos (π/(15)).cos ((2π)/(15)).cos ((3π)/(15)).cos ((4π)/(15)).cos ((5π)/(15)).cos ((6π)/(15)).cos ((7π)/(15))
$$\:{P}\:=\:\mathrm{cos}\:\frac{\pi}{\mathrm{15}}.\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{15}}.\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{15}}.\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{15}}.\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{15}}.\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{15}}.\mathrm{cos}\:\frac{\mathrm{7}\pi}{\mathrm{15}} \\ $$
Answered by EDWIN88 last updated on 26/Jan/21
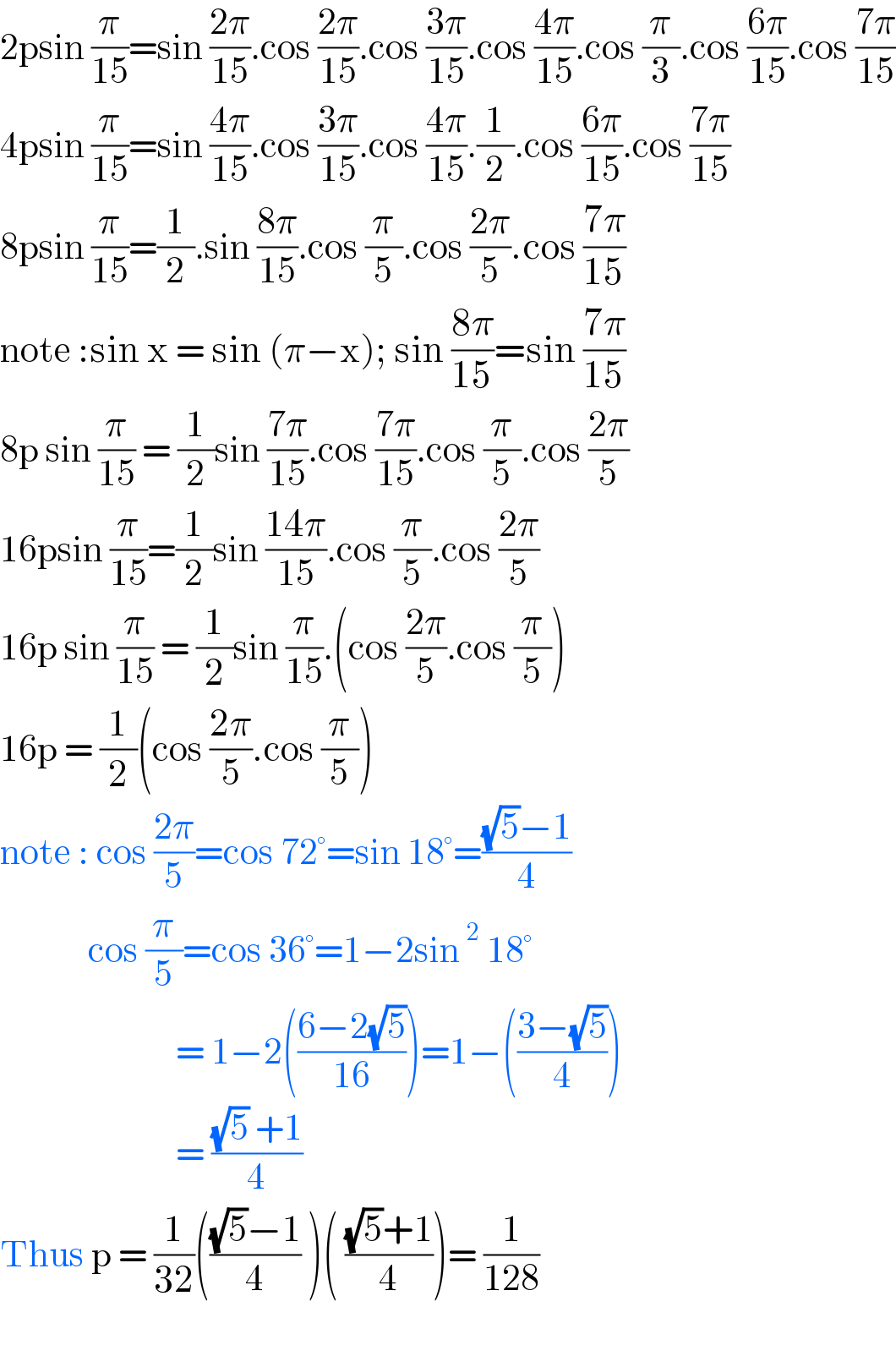
2psin (π/(15))=sin ((2π)/(15)).cos ((2π)/(15)).cos ((3π)/(15)).cos ((4π)/(15)).cos (π/3).cos ((6π)/(15)).cos ((7π)/(15)) 4psin (π/(15))=sin ((4π)/(15)).cos ((3π)/(15)).cos ((4π)/(15)).(1/2).cos ((6π)/(15)).cos ((7π)/(15)) 8psin (π/(15))=(1/2).sin ((8π)/(15)).cos (π/5).cos ((2π)/5).cos ((7π)/(15)) note :sin x = sin (π−x); sin ((8π)/(15))=sin ((7π)/(15)) 8p sin (π/(15)) = (1/2)sin ((7π)/(15)).cos ((7π)/(15)).cos (π/5).cos ((2π)/5) 16psin (π/(15))=(1/2)sin ((14π)/(15)).cos (π/5).cos ((2π)/5) 16p sin (π/(15)) = (1/2)sin (π/(15)).(cos ((2π)/5).cos (π/5)) 16p = (1/2)(cos ((2π)/5).cos (π/5)) note : cos ((2π)/5)=cos 72°=sin 18°=(((√5)−1)/4) cos (π/5)=cos 36°=1−2sin^2 18° = 1−2(((6−2(√5))/(16)))=1−(((3−(√5))/4)) = (((√5) +1)/4) Thus p = (1/(32))((((√5)−1)/4) )( (((√5)+1)/4))= (1/(128))
$$\mathrm{2psin}\:\frac{\pi}{\mathrm{15}}=\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{15}}.\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{15}}.\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{15}}.\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{15}}.\mathrm{cos}\:\frac{\pi}{\mathrm{3}}.\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{15}}.\mathrm{cos}\:\frac{\mathrm{7}\pi}{\mathrm{15}} \\ $$$$\mathrm{4psin}\:\frac{\pi}{\mathrm{15}}=\mathrm{sin}\:\frac{\mathrm{4}\pi}{\mathrm{15}}.\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{15}}.\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{15}}.\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{15}}.\mathrm{cos}\:\frac{\mathrm{7}\pi}{\mathrm{15}} \\ $$$$\mathrm{8psin}\:\frac{\pi}{\mathrm{15}}=\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{sin}\:\frac{\mathrm{8}\pi}{\mathrm{15}}.\mathrm{cos}\:\frac{\pi}{\mathrm{5}}.\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{5}}.\mathrm{cos}\:\frac{\mathrm{7}\pi}{\mathrm{15}} \\ $$$$\mathrm{note}\::\mathrm{sin}\:\mathrm{x}\:=\:\mathrm{sin}\:\left(\pi−\mathrm{x}\right);\:\mathrm{sin}\:\frac{\mathrm{8}\pi}{\mathrm{15}}=\mathrm{sin}\:\frac{\mathrm{7}\pi}{\mathrm{15}} \\ $$$$\mathrm{8p}\:\mathrm{sin}\:\frac{\pi}{\mathrm{15}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\frac{\mathrm{7}\pi}{\mathrm{15}}.\mathrm{cos}\:\frac{\mathrm{7}\pi}{\mathrm{15}}.\mathrm{cos}\:\frac{\pi}{\mathrm{5}}.\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{5}} \\ $$$$\mathrm{16psin}\:\frac{\pi}{\mathrm{15}}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\frac{\mathrm{14}\pi}{\mathrm{15}}.\mathrm{cos}\:\frac{\pi}{\mathrm{5}}.\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{5}} \\ $$$$\mathrm{16p}\:\mathrm{sin}\:\frac{\pi}{\mathrm{15}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\frac{\pi}{\mathrm{15}}.\left(\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{5}}.\mathrm{cos}\:\frac{\pi}{\mathrm{5}}\right) \\ $$$$\mathrm{16p}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{5}}.\mathrm{cos}\:\frac{\pi}{\mathrm{5}}\right) \\ $$$$\mathrm{note}\::\:\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{5}}=\mathrm{cos}\:\mathrm{72}°=\mathrm{sin}\:\mathrm{18}°=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:\frac{\pi}{\mathrm{5}}=\mathrm{cos}\:\mathrm{36}°=\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \:\mathrm{18}° \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{1}−\mathrm{2}\left(\frac{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}}\right)=\mathrm{1}−\left(\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{4}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\sqrt{\mathrm{5}}\:+\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{Thus}\:\mathrm{p}\:=\:\frac{\mathrm{1}}{\mathrm{32}}\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\:\right)\left(\:\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}}\right)=\:\frac{\mathrm{1}}{\mathrm{128}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *