Question Number 178388 by mathlove last updated on 16/Oct/22

$$\:{p}\left({sin}^{\mathrm{77}} \frac{\mathrm{50}}{\mathrm{19}},{cos}\frac{\mathrm{27}}{\mathrm{13}}\right) \\ $$$$\left.\mathrm{1}\left.\right)\left.\:\left.{VI}\:\:\:\:\mathrm{2}\right){III}\:\:\:\:\:\mathrm{3}\right){II}\:\:\:\:\:\:\:\mathrm{4}\right){I} \\ $$In which region of the fixed coordinate system is this point located?
Answered by saboorhalimi last updated on 16/Oct/22

$$\:{p}\left(+,\:−\right)\:\Rightarrow\:{IV}\: \\ $$
Commented by mathlove last updated on 16/Oct/22

$${pleas}\:{solve}\:{it} \\ $$
Answered by mr W last updated on 16/Oct/22
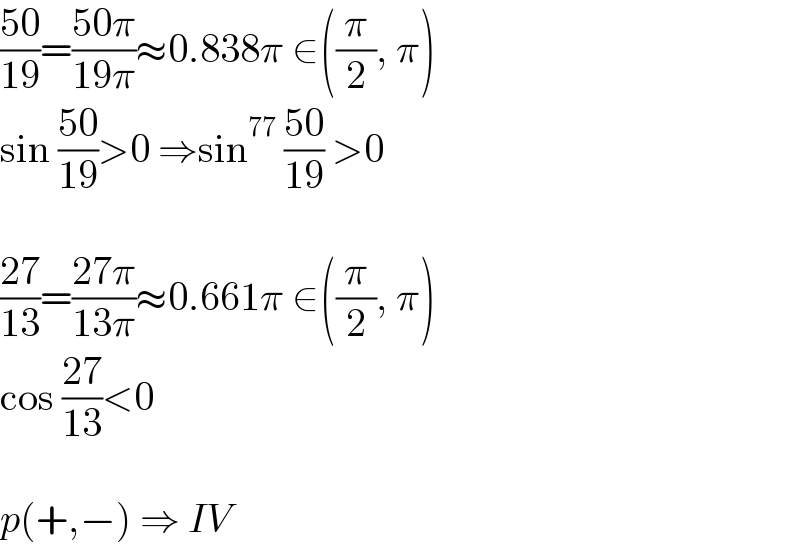
$$\frac{\mathrm{50}}{\mathrm{19}}=\frac{\mathrm{50}\pi}{\mathrm{19}\pi}\approx\mathrm{0}.\mathrm{838}\pi\:\in\left(\frac{\pi}{\mathrm{2}},\:\pi\right)\: \\ $$$$\mathrm{sin}\:\frac{\mathrm{50}}{\mathrm{19}}>\mathrm{0}\:\Rightarrow\mathrm{sin}^{\mathrm{77}} \:\frac{\mathrm{50}}{\mathrm{19}}\:>\mathrm{0} \\ $$$$ \\ $$$$\frac{\mathrm{27}}{\mathrm{13}}=\frac{\mathrm{27}\pi}{\mathrm{13}\pi}\approx\mathrm{0}.\mathrm{661}\pi\:\in\left(\frac{\pi}{\mathrm{2}},\:\pi\right) \\ $$$$\mathrm{cos}\:\frac{\mathrm{27}}{\mathrm{13}}<\mathrm{0} \\ $$$$ \\ $$$${p}\left(+,−\right)\:\Rightarrow\:{IV} \\ $$
Commented by mathlove last updated on 16/Oct/22

$${thanks}\:{a}\:{lot}\:{sir} \\ $$
