Question Number 95738 by bobhans last updated on 27/May/20
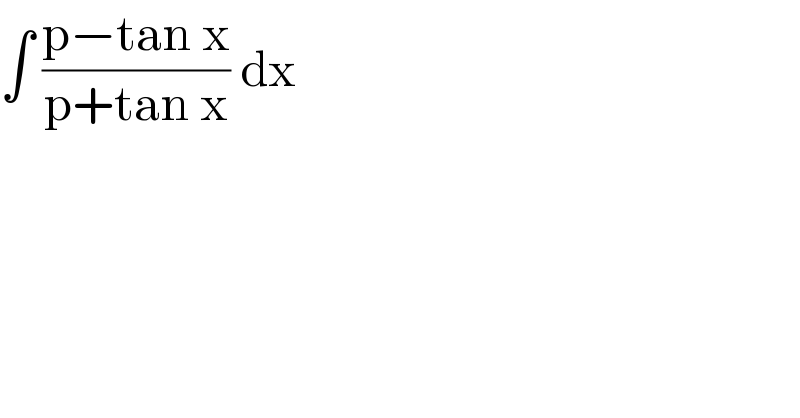
$$\int\:\frac{\mathrm{p}−\mathrm{tan}\:\mathrm{x}}{\mathrm{p}+\mathrm{tan}\:\mathrm{x}}\:\mathrm{dx}\: \\ $$
Commented by PRITHWISH SEN 2 last updated on 27/May/20

$$\frac{\mathrm{pcosx}−\mathrm{sin}\:\mathrm{x}}{\mathrm{pcos}\:\mathrm{x}+\mathrm{sin}\:\mathrm{x}}\:=\:\frac{\mathrm{m}\left(\mathrm{cos}\:\mathrm{x}−\mathrm{psin}\:\mathrm{x}\right)+\mathrm{n}\left(\mathrm{pcos}\:\mathrm{x}+\mathrm{sin}\:\mathrm{x}\right)}{\mathrm{pcos}\:\mathrm{x}+\mathrm{sin}\:\mathrm{x}} \\ $$$$\mathrm{m}=\frac{\mathrm{2p}}{\mathrm{1}+\mathrm{p}^{\mathrm{2}} } \\ $$$$\mathrm{n}=\frac{\mathrm{p}^{\mathrm{2}} −\mathrm{1}}{\mathrm{p}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\int\frac{\mathrm{p}−\mathrm{tan}\:\mathrm{x}}{\mathrm{p}+\mathrm{tan}\:\mathrm{x}}\mathrm{dx}=\frac{\mathrm{2p}}{\mathrm{1}+\mathrm{p}^{\mathrm{2}} }\int\frac{\mathrm{d}\left(\mathrm{pcos}\:\mathrm{x}+\mathrm{sin}\:\mathrm{x}\right)}{\mathrm{pcos}\:\mathrm{x}+\mathrm{sin}\:\mathrm{x}}\:+\frac{\mathrm{p}^{\mathrm{2}} −\mathrm{1}}{\mathrm{p}^{\mathrm{2}} +\mathrm{1}}\int\mathrm{dx} \\ $$$$=\frac{\mathrm{2}\boldsymbol{\mathrm{p}}}{\mathrm{1}+\boldsymbol{\mathrm{p}}^{\mathrm{2}} }\:\boldsymbol{\mathrm{ln}}\mid\boldsymbol{\mathrm{p}}\:\boldsymbol{\mathrm{cosx}}+\boldsymbol{\mathrm{sinx}}\mid+\frac{\boldsymbol{\mathrm{p}}^{\mathrm{2}} −\mathrm{1}}{\boldsymbol{\mathrm{p}}^{\mathrm{2}} +\mathrm{1}}.\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{C}} \\ $$$$\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}} \\ $$
Commented by bobhans last updated on 27/May/20

$$\mathrm{yes}..\mathrm{thx} \\ $$
Answered by mathmax by abdo last updated on 27/May/20

$$\mathrm{I}\:=\int\:\:\frac{\mathrm{p}−\mathrm{tanx}}{\mathrm{p}+\mathrm{tanx}}\mathrm{dx}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{tanx}\:=\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\frac{\mathrm{p}−\mathrm{t}}{\mathrm{p}+\mathrm{t}}×\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:=\int\:\:\frac{\mathrm{p}−\mathrm{t}}{\left(\mathrm{p}+\mathrm{t}\right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)}\mathrm{dt}\:\:\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{p}−\mathrm{t}}{\left(\mathrm{t}+\mathrm{p}\right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$\Rightarrow\mathrm{F}\left(\mathrm{t}\right)\:=\frac{\mathrm{a}}{\mathrm{t}+\mathrm{p}}\:\:+\frac{\mathrm{bt}\:+\mathrm{c}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\mathrm{a}\:=\frac{\mathrm{2p}}{\mathrm{p}^{\mathrm{2}} \:+\mathrm{1}}\:\:,\:\:\mathrm{lim}_{\mathrm{t}\rightarrow+\infty} \mathrm{tF}\left(\mathrm{t}\right)\:=\mathrm{0}\:=\mathrm{a}+\mathrm{b}\:\Rightarrow\mathrm{b}\:=−\frac{\mathrm{2p}}{\mathrm{p}^{\mathrm{2}} \:+\mathrm{1}}\: \\ $$$$\mathrm{F}\left(\mathrm{0}\right)=\mathrm{1}\:=\frac{\mathrm{a}}{\mathrm{p}}\:+\mathrm{c}\:\Rightarrow\mathrm{c}=\mathrm{1}−\frac{\mathrm{a}}{\mathrm{p}}\:=\mathrm{1}−\frac{\mathrm{2}}{\mathrm{p}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{2p}}{\left(\mathrm{p}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{t}+\mathrm{p}\right)}\:+\frac{\left(\frac{−\mathrm{2p}}{\mathrm{p}^{\mathrm{2}} \:+\mathrm{1}}\right)\mathrm{t}+\frac{\mathrm{p}^{\mathrm{2}} −\mathrm{1}}{\mathrm{p}^{\mathrm{2}} \:+\mathrm{1}}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\Rightarrow\mathrm{I}\:=\frac{\mathrm{2p}}{\left(\mathrm{p}^{\mathrm{2}} \:+\mathrm{1}\right)}\int\:\:\frac{\mathrm{dt}}{\mathrm{t}+\mathrm{p}}\:−\frac{\mathrm{1}}{\mathrm{p}^{\mathrm{2}} +\mathrm{1}}\int\:\:\frac{\mathrm{2pt}+\mathrm{1}−\mathrm{p}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt} \\ $$$$=\frac{\mathrm{2p}}{\mathrm{p}^{\mathrm{2}} +\mathrm{1}}\mathrm{ln}\mid\mathrm{t}+\mathrm{p}\mid−\frac{\mathrm{p}}{\mathrm{p}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)+\frac{\mathrm{p}^{\mathrm{2}} −\mathrm{1}}{\mathrm{p}^{\mathrm{2}} \:+\mathrm{1}}\:\mathrm{arctant}\:\:+\mathrm{C} \\ $$$$\mathrm{I}\:=\frac{\mathrm{2p}}{\mathrm{p}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{ln}\mid\mathrm{tanx}\:+\mathrm{p}\mid−\frac{\mathrm{p}}{\mathrm{p}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{ln}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)+\frac{\mathrm{p}^{\mathrm{2}} −\mathrm{1}}{\mathrm{p}^{\mathrm{2}\:} +\mathrm{1}}\:\mathrm{x}\:+\mathrm{C} \\ $$
Commented by bobhans last updated on 27/May/20

$$\mathrm{thx} \\ $$
