Question Number 172842 by cortano1 last updated on 02/Jul/22
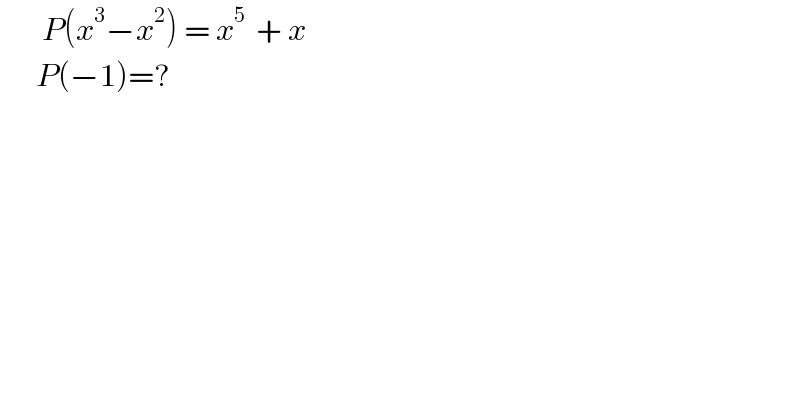
$$\:\:\:\:\:\:\:{P}\left({x}^{\mathrm{3}} −{x}^{\mathrm{2}} \right)\:=\:{x}^{\mathrm{5}\:} \:+\:{x}\: \\ $$$$\:\:\:\:\:\:{P}\left(−\mathrm{1}\right)=? \\ $$
Commented by greougoury555 last updated on 02/Jul/22
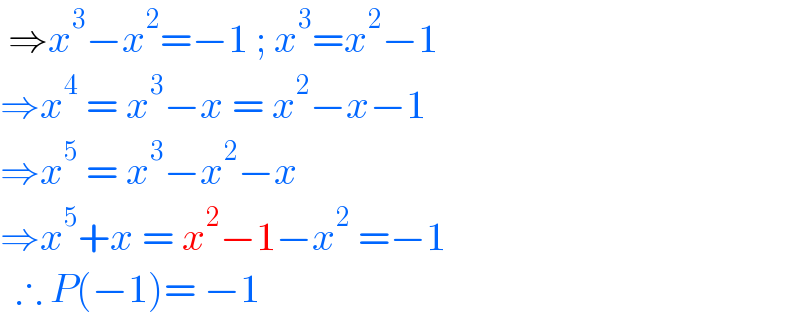
$$\:\Rightarrow{x}^{\mathrm{3}} −{x}^{\mathrm{2}} =−\mathrm{1}\:;\:{x}^{\mathrm{3}} ={x}^{\mathrm{2}} −\mathrm{1} \\ $$$$\Rightarrow{x}^{\mathrm{4}} \:=\:{x}^{\mathrm{3}} −{x}\:=\:{x}^{\mathrm{2}} −{x}−\mathrm{1} \\ $$$$\Rightarrow{x}^{\mathrm{5}} \:=\:{x}^{\mathrm{3}} −{x}^{\mathrm{2}} −{x} \\ $$$$\Rightarrow{x}^{\mathrm{5}} +{x}\:=\:{x}^{\mathrm{2}} −\mathrm{1}−{x}^{\mathrm{2}} \:=−\mathrm{1} \\ $$$$\:\:\therefore\:{P}\left(−\mathrm{1}\right)=\:−\mathrm{1} \\ $$
