Question Number 157184 by cortano last updated on 20/Oct/21
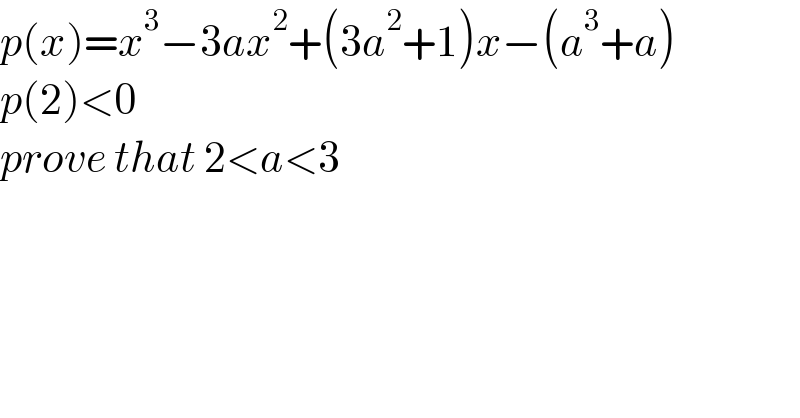
$${p}\left({x}\right)={x}^{\mathrm{3}} −\mathrm{3}{ax}^{\mathrm{2}} +\left(\mathrm{3}{a}^{\mathrm{2}} +\mathrm{1}\right){x}−\left({a}^{\mathrm{3}} +{a}\right) \\ $$$${p}\left(\mathrm{2}\right)<\mathrm{0} \\ $$$${prove}\:{that}\:\mathrm{2}<{a}<\mathrm{3} \\ $$
Answered by ghimisi last updated on 20/Oct/21
![p(x)=x^3 −3ax^2 +3a^2 x−x^3 +x−a=(x−a)^3 +x−a p(2)<0⇒(2−a)[(2−a)^2 +1]<0⇒a>2 a<3 ??????](https://www.tinkutara.com/question/Q157185.png)
$${p}\left({x}\right)={x}^{\mathrm{3}} −\mathrm{3}{ax}^{\mathrm{2}} +\mathrm{3}{a}^{\mathrm{2}} {x}−{x}^{\mathrm{3}} +{x}−{a}=\left({x}−{a}\right)^{\mathrm{3}} +{x}−{a} \\ $$$${p}\left(\mathrm{2}\right)<\mathrm{0}\Rightarrow\left(\mathrm{2}−{a}\right)\left[\left(\mathrm{2}−{a}\right)^{\mathrm{2}} +\mathrm{1}\right]<\mathrm{0}\Rightarrow{a}>\mathrm{2} \\ $$$${a}<\mathrm{3}\:\:\:\:?????? \\ $$
