Menu Close

P-z-az-3-z-2-a-6-z-b-6-P-z-z-2-4-Q-z-Find-a-b-

Tinku Tara 0 Comments
Pin




Question Number 144736 by mathdanisur last updated on 28/Jun/21
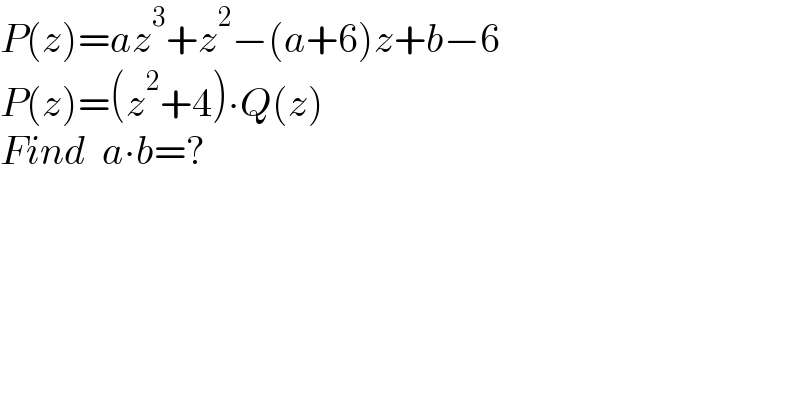
P(z)=az^3 +z^2 −(a+6)z+b−6 P(z)=(z^2 +4)∙Q(z) Find a∙b=?
$${P}\left({z}\right)={az}^{\mathrm{3}} +{z}^{\mathrm{2}} −\left({a}+\mathrm{6}\right){z}+{b}−\mathrm{6} \\ $$$${P}\left({z}\right)=\left({z}^{\mathrm{2}} +\mathrm{4}\right)\centerdot{Q}\left({z}\right) \\ $$$${Find}\:\:{a}\centerdot{b}=? \\ $$
Answered by nimnim last updated on 12/Mar/22
P(z)=az^3 +z^2 −(a+6)z+b−6 P(z)=(z^2 +4)Q(z) =(z^2 +4)(az+k) =az^3 +kz^2 +4az+4k ⇒k=1,4a=−(a+6), 4k=b−6 ⇒k=1,a=−(6/5), b=10 ∴ a.b=−(6/5).10=−12
$$\mathrm{P}\left(\mathrm{z}\right)=\mathrm{az}^{\mathrm{3}} +\mathrm{z}^{\mathrm{2}} −\left(\mathrm{a}+\mathrm{6}\right)\mathrm{z}+\mathrm{b}−\mathrm{6} \\ $$$$\mathrm{P}\left(\mathrm{z}\right)=\left(\mathrm{z}^{\mathrm{2}} +\mathrm{4}\right)\mathrm{Q}\left(\mathrm{z}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{z}^{\mathrm{2}} +\mathrm{4}\right)\left(\mathrm{az}+\mathrm{k}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{az}^{\mathrm{3}} +\mathrm{kz}^{\mathrm{2}} +\mathrm{4az}+\mathrm{4k} \\ $$$$\Rightarrow\mathrm{k}=\mathrm{1},\mathrm{4a}=−\left(\mathrm{a}+\mathrm{6}\right),\:\mathrm{4k}=\mathrm{b}−\mathrm{6} \\ $$$$\Rightarrow\mathrm{k}=\mathrm{1},\mathrm{a}=−\frac{\mathrm{6}}{\mathrm{5}},\:\:\mathrm{b}=\mathrm{10} \\ $$$$\therefore\:\mathrm{a}.\mathrm{b}=−\frac{\mathrm{6}}{\mathrm{5}}.\mathrm{10}=−\mathrm{12} \\ $$
Commented by mathdanisur last updated on 28/Jun/21
cool thanks Sir
$${cool}\:{thanks}\:{Sir} \\ $$
Answered by imjagoll last updated on 28/Jun/21
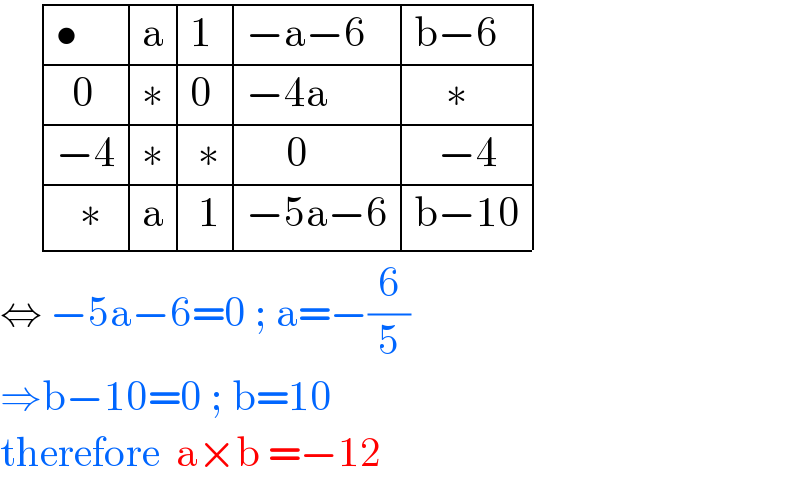
determinant ((•,a,1,(−a−6),(b−6)),(( 0),∗,0,(−4a),( ∗)),((−4),∗,( ∗),( 0),( −4)),(( ∗),a,( 1),(−5a−6),(b−10))) ⇔ −5a−6=0 ; a=−(6/5) ⇒b−10=0 ; b=10 therefore a×b =−12
$$\:\:\:\:\begin{array}{|c|c|c|c|}{\bullet}&\hline{\mathrm{a}}&\hline{\mathrm{1}}&\hline{−\mathrm{a}−\mathrm{6}}&\hline{\mathrm{b}−\mathrm{6}}\\{\:\:\mathrm{0}}&\hline{\ast}&\hline{\mathrm{0}}&\hline{−\mathrm{4a}}&\hline{\:\:\:\:\ast}\\{−\mathrm{4}}&\hline{\ast}&\hline{\:\ast}&\hline{\:\:\:\:\:\mathrm{0}}&\hline{\:\:\:−\mathrm{4}}\\{\:\:\:\ast}&\hline{\mathrm{a}}&\hline{\:\mathrm{1}}&\hline{−\mathrm{5a}−\mathrm{6}}&\hline{\mathrm{b}−\mathrm{10}}\\\hline\end{array} \\ $$$$\Leftrightarrow\:−\mathrm{5a}−\mathrm{6}=\mathrm{0}\:;\:\mathrm{a}=−\frac{\mathrm{6}}{\mathrm{5}} \\ $$$$\Rightarrow\mathrm{b}−\mathrm{10}=\mathrm{0}\:;\:\mathrm{b}=\mathrm{10}\: \\ $$$$\mathrm{therefore}\:\:\mathrm{a}×\mathrm{b}\:=−\mathrm{12} \\ $$
Commented by mathdanisur last updated on 28/Jun/21
cool solution thanks Sir
$${cool}\:{solution}\:{thanks}\:{Sir} \\ $$
Commented by Rasheed.Sindhi last updated on 28/Jun/21
imjagoll sir, I′m interested in your method. Please clerify how have you made the table?
$${imjagoll}\:{sir},\:{I}'{m}\:{interested}\:{in} \\ $$$${your}\:{method}.\:{Please}\:{clerify}\:{how} \\ $$$${have}\:{you}\:{made}\:{the}\:{table}? \\ $$
Commented by liberty last updated on 29/Jun/21
i think this is by Horner′s Theorem
$$\mathrm{i}\:\mathrm{think}\:\mathrm{this}\:\mathrm{is}\:\mathrm{by}\:\mathrm{Horner}'\mathrm{s}\:\mathrm{Theorem}\: \\ $$
Commented by imjagoll last updated on 29/Jun/21
yes
$$\mathrm{yes} \\ $$
Commented by Rasheed.Sindhi last updated on 29/Jun/21
ThαnX both sirs!
$$\mathcal{T}{h}\alpha{n}\mathcal{X}\:\:{both}\:{sirs}! \\ $$
Answered by Rasheed.Sindhi last updated on 28/Jun/21
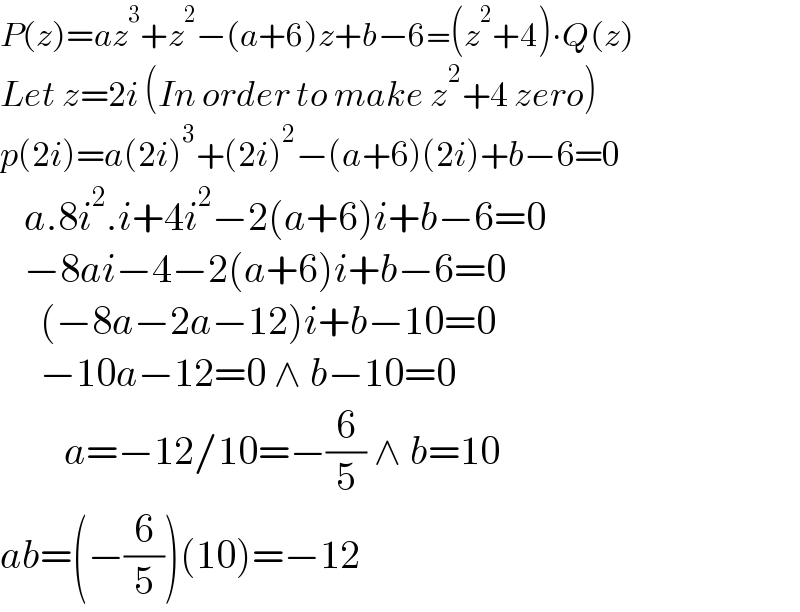
P(z)=az^3 +z^2 −(a+6)z+b−6=(z^2 +4)∙Q(z) Let z=2i (In order to make z^2 +4 zero) p(2i)=a(2i)^3 +(2i)^2 −(a+6)(2i)+b−6=0 a.8i^2 .i+4i^2 −2(a+6)i+b−6=0 −8ai−4−2(a+6)i+b−6=0 (−8a−2a−12)i+b−10=0 −10a−12=0 ∧ b−10=0 a=−12/10=−(6/5) ∧ b=10 ab=(−(6/5))(10)=−12
$${P}\left({z}\right)={az}^{\mathrm{3}} +{z}^{\mathrm{2}} −\left({a}+\mathrm{6}\right){z}+{b}−\mathrm{6}=\left({z}^{\mathrm{2}} +\mathrm{4}\right)\centerdot{Q}\left({z}\right) \\ $$$${Let}\:{z}=\mathrm{2}{i}\:\left({In}\:{order}\:{to}\:{make}\:{z}^{\mathrm{2}} +\mathrm{4}\:{zero}\right) \\ $$$${p}\left(\mathrm{2}{i}\right)={a}\left(\mathrm{2}{i}\right)^{\mathrm{3}} +\left(\mathrm{2}{i}\right)^{\mathrm{2}} −\left({a}+\mathrm{6}\right)\left(\mathrm{2}{i}\right)+{b}−\mathrm{6}=\mathrm{0} \\ $$$$\:\:\:{a}.\mathrm{8}{i}^{\mathrm{2}} .{i}+\mathrm{4}{i}^{\mathrm{2}} −\mathrm{2}\left({a}+\mathrm{6}\right){i}+{b}−\mathrm{6}=\mathrm{0} \\ $$$$\:\:\:−\mathrm{8}{ai}−\mathrm{4}−\mathrm{2}\left({a}+\mathrm{6}\right){i}+{b}−\mathrm{6}=\mathrm{0} \\ $$$$\:\:\:\:\:\left(−\mathrm{8}{a}−\mathrm{2}{a}−\mathrm{12}\right){i}+{b}−\mathrm{10}=\mathrm{0} \\ $$$$\:\:\:\:\:−\mathrm{10}{a}−\mathrm{12}=\mathrm{0}\:\wedge\:{b}−\mathrm{10}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:{a}=−\mathrm{12}/\mathrm{10}=−\frac{\mathrm{6}}{\mathrm{5}}\:\wedge\:{b}=\mathrm{10} \\ $$$${ab}=\left(−\frac{\mathrm{6}}{\mathrm{5}}\right)\left(\mathrm{10}\right)=−\mathrm{12} \\ $$
Commented by mathdanisur last updated on 28/Jun/21
cool solution Sir thanks
$${cool}\:{solution}\:{Sir}\:{thanks} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *