Question Number 167853 by LEKOUMA last updated on 27/Mar/22
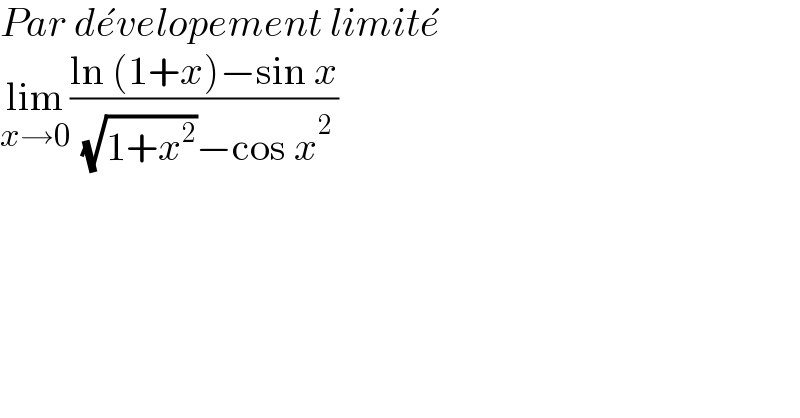
$${Par}\:{d}\acute {{e}velopement}\:{limit}\acute {{e}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{ln}\:\left(\mathrm{1}+{x}\right)−\mathrm{sin}\:{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }−\mathrm{cos}\:{x}^{\mathrm{2}} } \\ $$
Answered by qaz last updated on 27/Mar/22
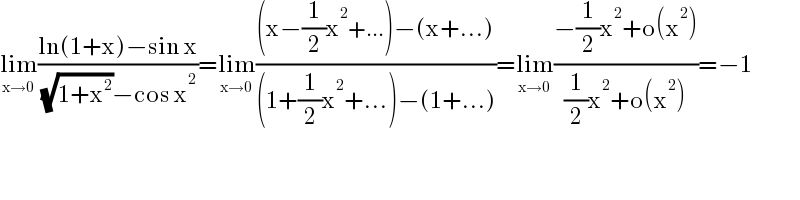
$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)−\mathrm{sin}\:\mathrm{x}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }−\mathrm{cos}\:\mathrm{x}^{\mathrm{2}} }=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +…\right)−\left(\mathrm{x}+…\right)}{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +…\right)−\left(\mathrm{1}+…\right)}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +\mathrm{o}\left(\mathrm{x}^{\mathrm{2}} \right)}{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +\mathrm{o}\left(\mathrm{x}^{\mathrm{2}} \right)}=−\mathrm{1} \\ $$
Commented by LEKOUMA last updated on 27/Mar/22

$${X}+…? \\ $$$$\left(\mathrm{1}+…\right)? \\ $$
Commented by qaz last updated on 27/Mar/22
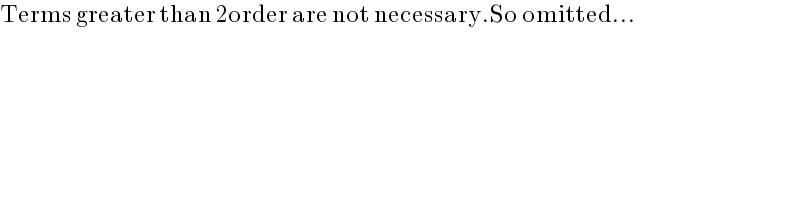
$$\mathrm{Terms}\:\mathrm{greater}\:\mathrm{than}\:\mathrm{2order}\:\mathrm{are}\:\mathrm{not}\:\mathrm{necessary}.\mathrm{So}\:\mathrm{omitted}… \\ $$
