Question Number 20241 by tammi last updated on 24/Aug/17

$${partial}\:{fraction} \\ $$$$\int\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{5}{x}−\mathrm{9}}{\:\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}{dx} \\ $$
Answered by $@ty@m last updated on 25/Aug/17
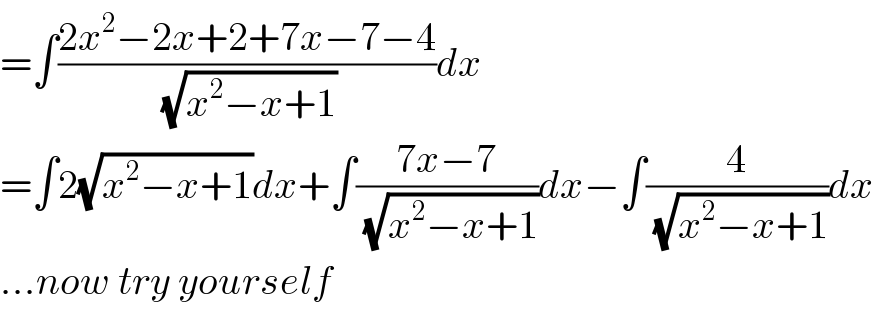
$$=\int\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{2}+\mathrm{7}{x}−\mathrm{7}−\mathrm{4}}{\:\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}{dx} \\ $$$$=\int\mathrm{2}\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}+\int\frac{\mathrm{7}{x}−\mathrm{7}}{\:\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}{dx}−\int\frac{\mathrm{4}}{\:\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}{dx} \\ $$$$…{now}\:{try}\:{yourself} \\ $$
