Question Number 16136 by Tinkutara last updated on 18/Jun/17

$$\mathrm{Photoelectric}\:\mathrm{emission}\:\mathrm{is}\:\mathrm{observed}\:\mathrm{from} \\ $$$$\mathrm{a}\:\mathrm{surface}\:\mathrm{when}\:\mathrm{lights}\:\mathrm{of}\:\mathrm{frequency}\:{n}_{\mathrm{1}} \\ $$$$\mathrm{and}\:{n}_{\mathrm{2}} \:\mathrm{incident}.\:\mathrm{If}\:\mathrm{the}\:\mathrm{ratio}\:\mathrm{of}\:\mathrm{maximum} \\ $$$$\mathrm{kinetic}\:\mathrm{energy}\:\mathrm{in}\:\mathrm{two}\:\mathrm{cases}\:\mathrm{is}\:\mathrm{K}\::\:\mathrm{1} \\ $$$$\mathrm{then}\:\left(\mathrm{Assume}\:{n}_{\mathrm{1}} \:>\:{n}_{\mathrm{2}} \right)\:\mathrm{threshold} \\ $$$$\mathrm{frequency}\:\mathrm{is} \\ $$$$\left(\mathrm{1}\right)\:\left(\mathrm{K}\:−\:\mathrm{1}\right)\:×\:\left(\mathrm{K}{n}_{\mathrm{2}} \:−\:{n}_{\mathrm{1}} \right) \\ $$$$\left(\mathrm{2}\right)\:\frac{\mathrm{K}{n}_{\mathrm{1}} \:−\:{n}_{\mathrm{2}} }{\mathrm{1}\:−\:\mathrm{K}} \\ $$$$\left(\mathrm{3}\right)\:\frac{\mathrm{K}\:−\:\mathrm{1}}{\mathrm{K}{n}_{\mathrm{1}} \:−\:{n}_{\mathrm{2}} } \\ $$$$\left(\mathrm{4}\right)\:\frac{\mathrm{K}{n}_{\mathrm{2}} \:−\:{n}_{\mathrm{1}} }{\mathrm{K}\:−\:\mathrm{1}} \\ $$
Answered by ajfour last updated on 18/Jun/17
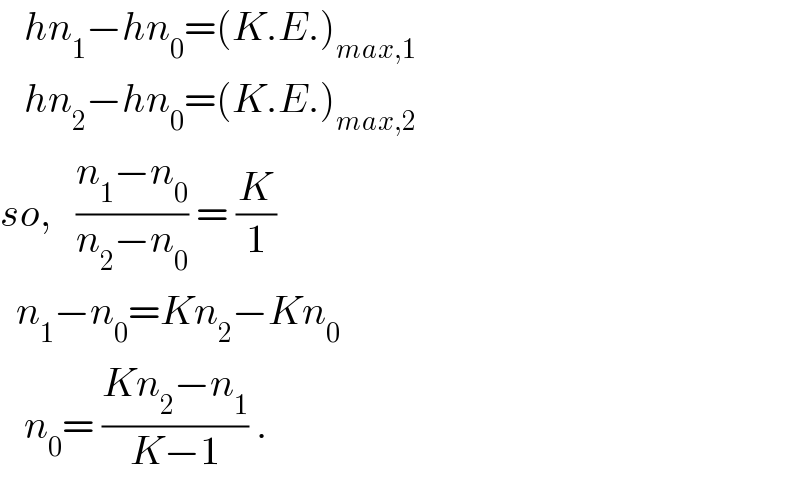
$$\:\:\:{hn}_{\mathrm{1}} −{hn}_{\mathrm{0}} =\left({K}.{E}.\right)_{{max},\mathrm{1}} \\ $$$$\:\:\:{hn}_{\mathrm{2}} −{hn}_{\mathrm{0}} =\left({K}.{E}.\right)_{{max},\mathrm{2}} \\ $$$${so},\:\:\:\frac{{n}_{\mathrm{1}} −{n}_{\mathrm{0}} }{{n}_{\mathrm{2}} −{n}_{\mathrm{0}} }\:=\:\frac{{K}}{\mathrm{1}} \\ $$$$\:\:{n}_{\mathrm{1}} −{n}_{\mathrm{0}} ={Kn}_{\mathrm{2}} −{Kn}_{\mathrm{0}} \\ $$$$\:\:\:{n}_{\mathrm{0}} =\:\frac{{Kn}_{\mathrm{2}} −{n}_{\mathrm{1}} }{{K}−\mathrm{1}}\:. \\ $$
