Question Number 89946 by jagoll last updated on 20/Apr/20
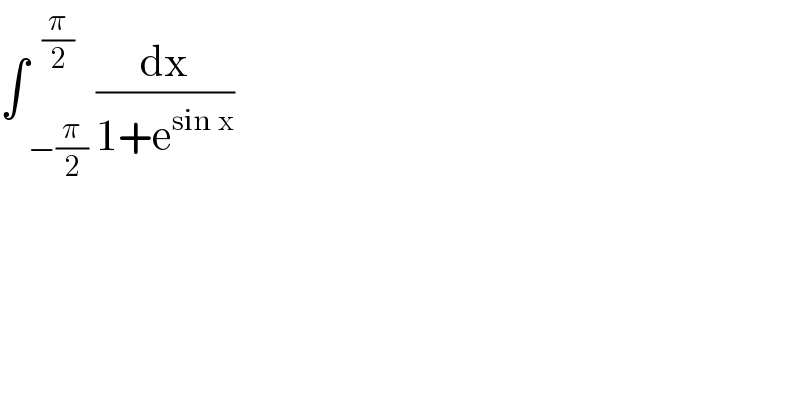
$$\int\underset{−\frac{\pi}{\mathrm{2}}} {\overset{\frac{\pi}{\mathrm{2}}} {\:}}\:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{e}^{\mathrm{sin}\:\mathrm{x}} } \\ $$
Answered by john santu last updated on 20/Apr/20
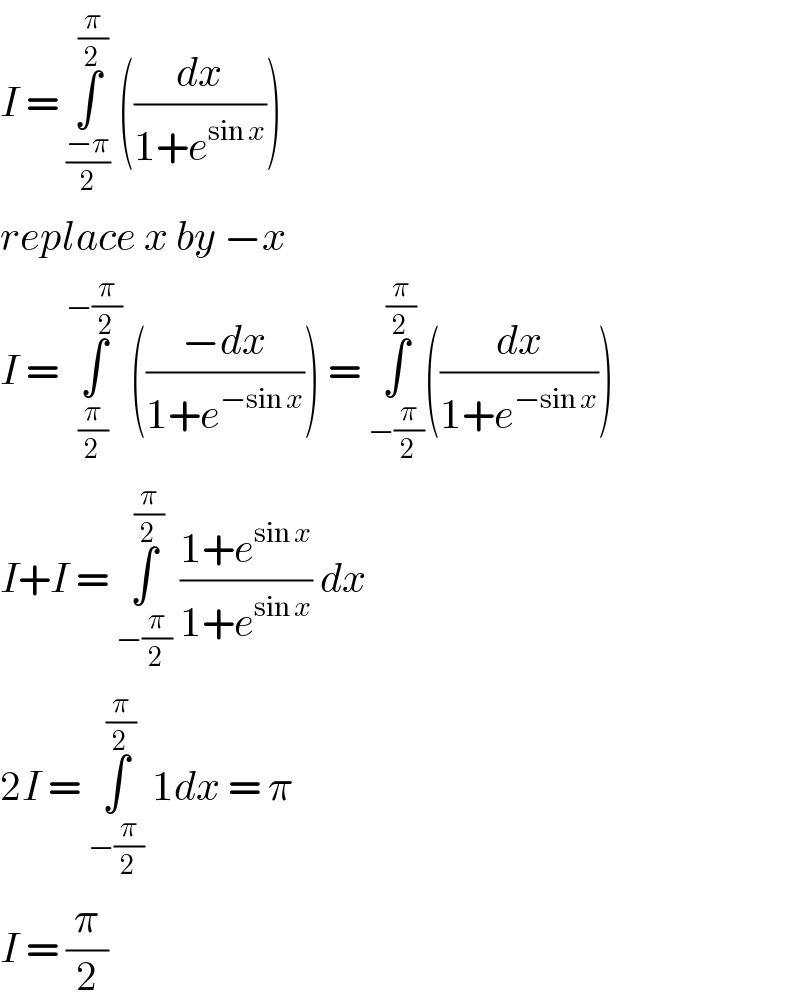
$${I}\:=\:\underset{\frac{−\pi}{\mathrm{2}}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\left(\frac{{dx}}{\mathrm{1}+{e}^{\mathrm{sin}\:{x}} }\right)\: \\ $$$${replace}\:{x}\:{by}\:−{x}\: \\ $$$${I}\:=\:\underset{\frac{\pi}{\mathrm{2}}} {\overset{−\frac{\pi}{\mathrm{2}}} {\int}}\:\left(\frac{−{dx}}{\mathrm{1}+{e}^{−\mathrm{sin}\:{x}} }\right)\:=\:\underset{−\frac{\pi}{\mathrm{2}}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\left(\frac{{dx}}{\mathrm{1}+{e}^{−\mathrm{sin}\:{x}} }\right) \\ $$$${I}+{I}\:=\:\underset{−\frac{\pi}{\mathrm{2}}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{\mathrm{1}+{e}^{\mathrm{sin}\:{x}} }{\mathrm{1}+{e}^{\mathrm{sin}\:{x}} }\:{dx} \\ $$$$\mathrm{2}{I}\:=\:\underset{−\frac{\pi}{\mathrm{2}}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\mathrm{1}{dx}\:=\:\pi \\ $$$${I}\:=\:\frac{\pi}{\mathrm{2}} \\ $$
