Question Number 87977 by Ar Brandon last updated on 07/Apr/20
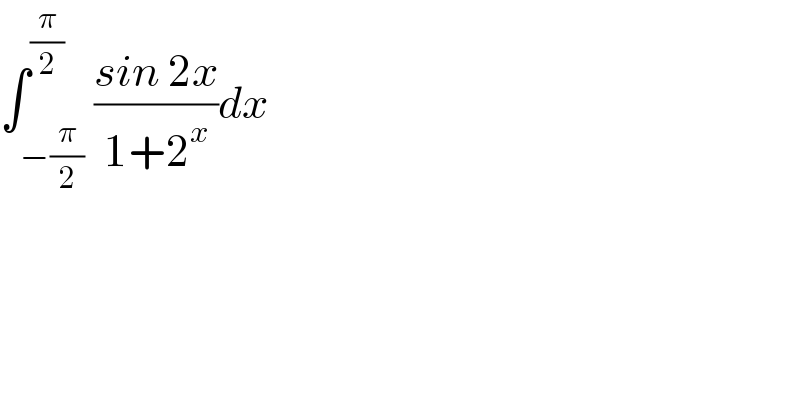
$$\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}\:\mathrm{2}{x}}{\mathrm{1}+\mathrm{2}^{{x}} }{dx} \\ $$
Commented by abdomathmax last updated on 08/Apr/20
![at form of serie ∫_(−(π/2)) ^(π/2) ((sin(2x))/(1+2^x ))dx =∫_(−(π/2)) ^(π/2) ((2^(−x) sin(2x))/(1+2^(−x) ))dx =∫_(−(π/2)) ^(π/2) 2^(−x) sin(2x)Σ_(n=0) ^∞ (−1)^n 2^(−nx) dx =Σ_(n=0) ^∞ (−1)^n ∫_(−(π/2)) ^(π/2) 2^(−(n+1)x) sin(2x)dx but ∫_(−(π/2)) ^(π/2) 2^(−(n+1)x) sin(2x)dx =Im(∫_(−(π/2)) ^(π/2) 2^(−(n+1)x) e^(2ix) dx) ∫_(−(π/2)) ^(π/2) e^(−(n+1)xln2 +2ix) dx =∫_(−(π/2)) ^(π/2) e^((2i−(n+1)ln2)x) dx =[(1/(2i−(n+1)ln2)) e^((2i−(n+1)ln2)x) ]_(−(π/2)) ^(π/2) =(1/(2i−(n+1)ln2)){ −e^(−(n+1)ln2(π/2)) −e^((n+1)ln2(π/2)) } =(((n+1)ln2−2i)/((n+1)^2 ln^2 2+4)){ e^((π/2)(n+1)ln2) +e^(−(π/2)(n+1)ln2) } ⇒ Im(...) =−(2/((n+1)^2 ln^2 2+4)) ×2 ch((π/2)(n+1)ln2) ⇒ ⇒ I =4Σ_(n=0) ^∞ (((−1)^(n+1) )/((n+1)^2 ln^2 2 +4))×ch((π/2)(n+1)ln2)](https://www.tinkutara.com/question/Q88058.png)
$${at}\:{form}\:{of}\:{serie} \\ $$$$\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{1}+\mathrm{2}^{{x}} }{dx}\:=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{2}^{−{x}} {sin}\left(\mathrm{2}{x}\right)}{\mathrm{1}+\mathrm{2}^{−{x}} }{dx} \\ $$$$=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{2}^{−{x}} {sin}\left(\mathrm{2}{x}\right)\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:\mathrm{2}^{−{nx}} \:{dx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{2}^{−\left({n}+\mathrm{1}\right){x}} \:{sin}\left(\mathrm{2}{x}\right){dx} \\ $$$${but}\:\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{2}^{−\left({n}+\mathrm{1}\right){x}} \:{sin}\left(\mathrm{2}{x}\right){dx} \\ $$$$={Im}\left(\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{2}^{−\left({n}+\mathrm{1}\right){x}} \:{e}^{\mathrm{2}{ix}} \:{dx}\right) \\ $$$$\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:{e}^{−\left({n}+\mathrm{1}\right){xln}\mathrm{2}\:+\mathrm{2}{ix}} \:{dx} \\ $$$$=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:{e}^{\left(\mathrm{2}{i}−\left({n}+\mathrm{1}\right){ln}\mathrm{2}\right){x}} \:{dx} \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{2}{i}−\left({n}+\mathrm{1}\right){ln}\mathrm{2}}\:{e}^{\left(\mathrm{2}{i}−\left({n}+\mathrm{1}\right){ln}\mathrm{2}\right){x}} \right]_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}−\left({n}+\mathrm{1}\right){ln}\mathrm{2}}\left\{\:−{e}^{−\left({n}+\mathrm{1}\right){ln}\mathrm{2}\frac{\pi}{\mathrm{2}}} −{e}^{\left({n}+\mathrm{1}\right){ln}\mathrm{2}\frac{\pi}{\mathrm{2}}} \right\} \\ $$$$=\frac{\left({n}+\mathrm{1}\right){ln}\mathrm{2}−\mathrm{2}{i}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} {ln}^{\mathrm{2}} \mathrm{2}+\mathrm{4}}\left\{\:{e}^{\frac{\pi}{\mathrm{2}}\left({n}+\mathrm{1}\right){ln}\mathrm{2}} \:+{e}^{−\frac{\pi}{\mathrm{2}}\left({n}+\mathrm{1}\right){ln}\mathrm{2}} \right\}\:\Rightarrow \\ $$$${Im}\left(…\right)\:=−\frac{\mathrm{2}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} {ln}^{\mathrm{2}} \mathrm{2}+\mathrm{4}}\:×\mathrm{2}\:{ch}\left(\frac{\pi}{\mathrm{2}}\left({n}+\mathrm{1}\right){ln}\mathrm{2}\right)\:\Rightarrow \\ $$$$\Rightarrow \\ $$$${I}\:=\mathrm{4}\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)^{\mathrm{2}} {ln}^{\mathrm{2}} \mathrm{2}\:+\mathrm{4}}×{ch}\left(\frac{\pi}{\mathrm{2}}\left({n}+\mathrm{1}\right){ln}\mathrm{2}\right) \\ $$
Commented by Ar Brandon last updated on 08/Apr/20

$${Amazing}!!!!! \\ $$
