Question Number 156240 by SANOGO last updated on 09/Oct/21
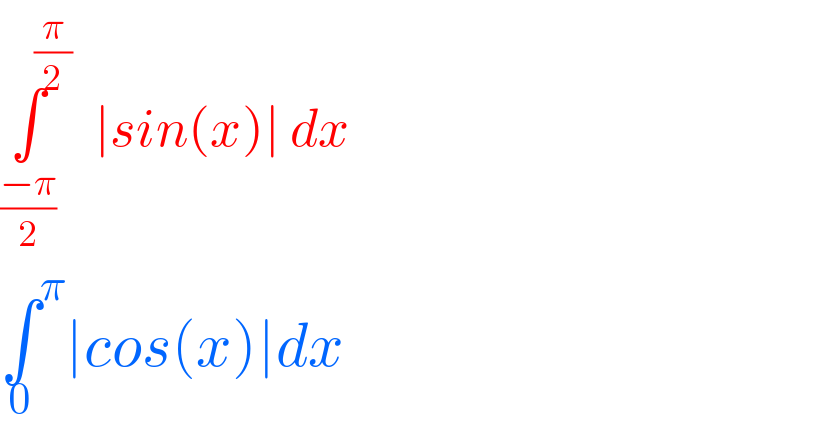
$$\underset{\frac{−\pi}{\mathrm{2}}} {\int}^{\frac{\pi}{\mathrm{2}}} \mid{sin}\left({x}\right)\mid\:{dx} \\ $$$$\underset{\mathrm{0}} {\int}^{\pi} \mid{cos}\left({x}\right)\mid{dx} \\ $$
Commented by SANOGO last updated on 09/Oct/21
$${merci}\:{bien}\:{le}\:{dur} \\ $$
Commented by tabata last updated on 09/Oct/21
$$\boldsymbol{{you}}\:\boldsymbol{{are}}\:\boldsymbol{{welcome}} \\ $$
Commented by tabata last updated on 09/Oct/21
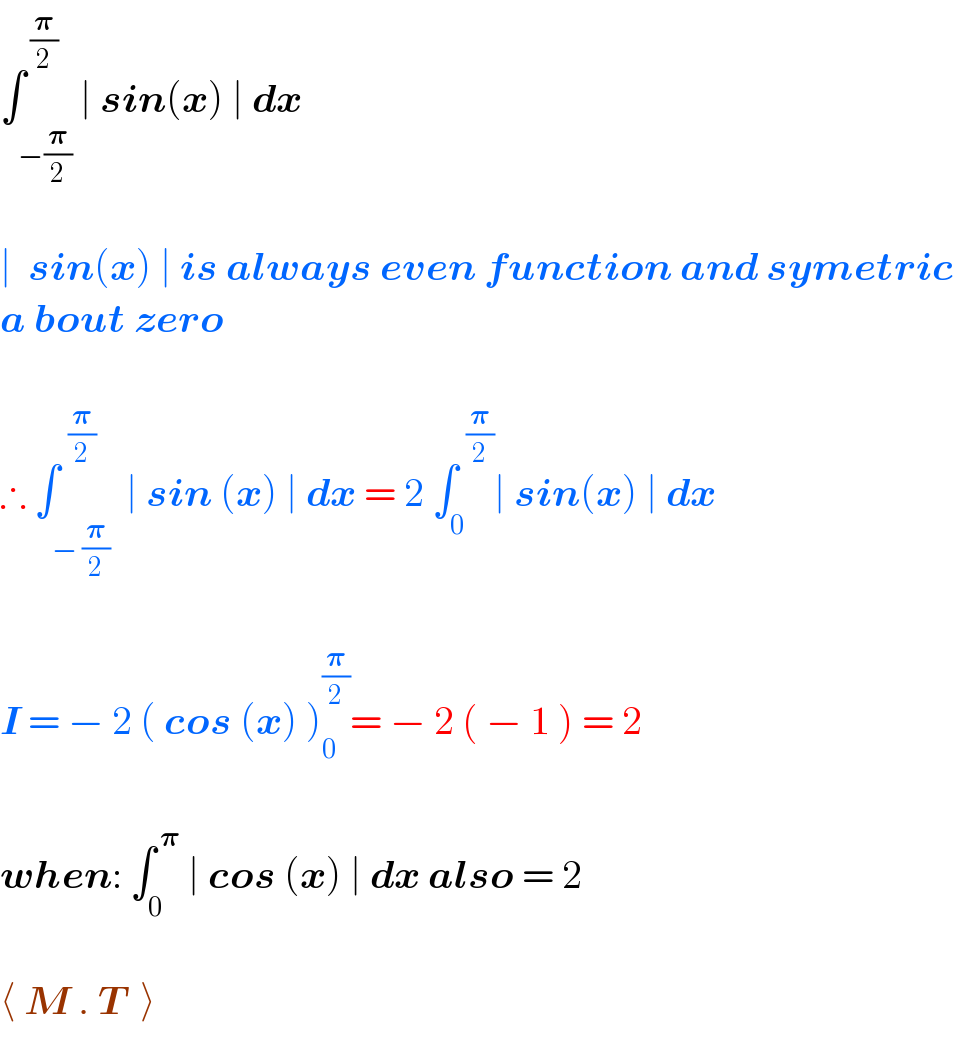
$$\int_{−\frac{\boldsymbol{\pi}}{\mathrm{2}}} ^{\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} \mid\:\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)\:\mid\:\boldsymbol{{dx}} \\ $$$$ \\ $$$$\mid\:\:\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)\:\mid\:\boldsymbol{{is}}\:\boldsymbol{{always}}\:\boldsymbol{{even}}\:\boldsymbol{{function}}\:\boldsymbol{{and}}\:\boldsymbol{{symetric}}\: \\ $$$$\boldsymbol{{a}}\:\boldsymbol{{bout}}\:\boldsymbol{{zero}}\: \\ $$$$ \\ $$$$\therefore\:\int_{−\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} ^{\:\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} \:\mid\:\boldsymbol{{sin}}\:\left(\boldsymbol{{x}}\right)\:\mid\:\boldsymbol{{dx}}\:=\:\mathrm{2}\:\int_{\mathrm{0}} ^{\:\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} \mid\:\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)\:\mid\:\boldsymbol{{dx}}\: \\ $$$$ \\ $$$$\boldsymbol{{I}}\:=\:−\:\mathrm{2}\:\left(\:\boldsymbol{{cos}}\:\left(\boldsymbol{{x}}\right)\:\right)_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} =\:−\:\mathrm{2}\:\left(\:−\:\mathrm{1}\:\right)\:=\:\mathrm{2} \\ $$$$ \\ $$$$\boldsymbol{{when}}:\:\int_{\mathrm{0}} ^{\:\boldsymbol{\pi}} \:\mid\:\boldsymbol{{cos}}\:\left(\boldsymbol{{x}}\right)\:\mid\:\boldsymbol{{dx}}\:\boldsymbol{{also}}\:=\:\mathrm{2} \\ $$$$ \\ $$$$\langle\:\boldsymbol{{M}}\:.\:\boldsymbol{{T}}\:\:\rangle \\ $$
