Question Number 117176 by bemath last updated on 10/Oct/20
$$\underset{\pi/\mathrm{4}} {\overset{\pi/\mathrm{2}} {\int}}\:\frac{\mathrm{4cot}\:{x}+\mathrm{1}\:}{\mathrm{4}−\mathrm{cot}\:{x}}\:{dx}\:=? \\ $$
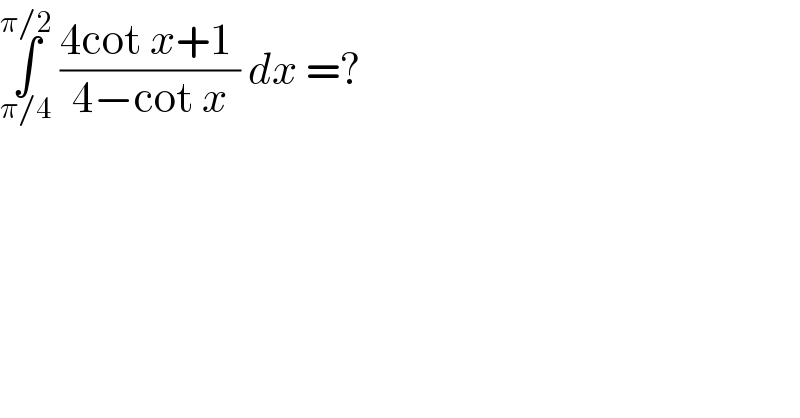
Commented by bemath last updated on 10/Oct/20
![the other way ((4cot x+1)/(4−cot x)) = cot (x−cot^(−1) (4)) ∫_(π/4) ^(π/2) ((4cot x+1)/(4−cot x)) dx = [ ln (sin (x−cot^(−1) (4))]_(π/4) ^(π/2) = ln (sin ((π/2)−cot^(−1) (4))−ln (sin ((π/4)−cot^(−1) (4)) = ln (((cos (cot^(−1) (4)))/(sin ((π/4)−cot^(−1) (4)))) = ln (((4/( (√(17))))/(((√2)/2)((4/( (√(17))))−(1/( (√(17)))))))) = ln (((4(√2))/3))](https://www.tinkutara.com/question/Q117180.png)
$${the}\:{other}\:{way}\: \\ $$$$\frac{\mathrm{4cot}\:{x}+\mathrm{1}}{\mathrm{4}−\mathrm{cot}\:{x}}\:=\:\mathrm{cot}\:\left({x}−\mathrm{cot}^{−\mathrm{1}} \left(\mathrm{4}\right)\right) \\ $$$$\underset{\pi/\mathrm{4}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\mathrm{4cot}\:{x}+\mathrm{1}}{\mathrm{4}−\mathrm{cot}\:{x}}\:{dx}\:=\:\left[\:\mathrm{ln}\:\left(\mathrm{sin}\:\left({x}−\mathrm{cot}^{−\mathrm{1}} \left(\mathrm{4}\right)\right)\right]_{\pi/\mathrm{4}} ^{\pi/\mathrm{2}} \right. \\ $$$$=\:\mathrm{ln}\:\left(\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\mathrm{cot}^{−\mathrm{1}} \left(\mathrm{4}\right)\right)−\mathrm{ln}\:\left(\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}−\mathrm{cot}^{−\mathrm{1}} \left(\mathrm{4}\right)\right)\right.\right. \\ $$$$=\:\mathrm{ln}\:\left(\frac{\mathrm{cos}\:\left(\mathrm{cot}^{−\mathrm{1}} \left(\mathrm{4}\right)\right)}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}−\mathrm{cot}^{−\mathrm{1}} \left(\mathrm{4}\right)\right.}\right)\: \\ $$$$=\:\mathrm{ln}\:\left(\frac{\frac{\mathrm{4}}{\:\sqrt{\mathrm{17}}}}{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\frac{\mathrm{4}}{\:\sqrt{\mathrm{17}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{17}}}\right)}\right) \\ $$$$=\:\mathrm{ln}\:\left(\frac{\mathrm{4}\sqrt{\mathrm{2}}}{\mathrm{3}}\right) \\ $$
Answered by TANMAY PANACEA last updated on 10/Oct/20
$$\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{4}{cosx}+{sinx}}{\mathrm{4}{sinx}−{cosx}}{dx} \\ $$$$\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{d}\left(\mathrm{4}{sinx}−{cosx}\right)}{\mathrm{4}{sinx}−{cosx}} \\ $$$$\mid{ln}\left(\mathrm{4}{sinx}−{cosx}\right)\mid_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \: \\ $$$$={ln}\left(\mathrm{4}−\mathrm{0}\right)−{ln}\left(\mathrm{4}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right) \\ $$$${ln}\left(\frac{\mathrm{4}\sqrt{\mathrm{2}}}{\mathrm{3}}\right) \\ $$
Commented by bemath last updated on 10/Oct/20
$${thank}\:{you}\:{sir} \\ $$
Answered by AbduraufKodiriy last updated on 10/Oct/20
$$\boldsymbol{{Solution}}: \\ $$$$\boldsymbol{{I}}=\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{4}\boldsymbol{{cot}}\left(\boldsymbol{{x}}\right)+\mathrm{1}}{\mathrm{4}−\boldsymbol{{cot}}\left(\boldsymbol{{x}}\right)}\boldsymbol{{dx}}=\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \boldsymbol{{cot}}\left(\boldsymbol{{x}}−\boldsymbol{{arccot}}\mathrm{4}\right)\boldsymbol{{dx}}= \\ $$$$=\boldsymbol{{ln}}\mid\boldsymbol{{sin}}\left(\boldsymbol{{x}}−\boldsymbol{{arccot}}\mathrm{4}\right)\mid\mid_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} =\boldsymbol{{ln}}\left(\frac{\boldsymbol{{sin}}\left(\frac{\pi}{\mathrm{2}}−\boldsymbol{{arccot}}\mathrm{4}\right)}{\boldsymbol{{sin}}\left(\frac{\pi}{\mathrm{4}}−\boldsymbol{{arccot}}\mathrm{4}\right)}\right)= \\ $$$$=\boldsymbol{{ln}}\left(\frac{\boldsymbol{{cos}}\left(\boldsymbol{{arccos}}\frac{\mathrm{4}}{\:\sqrt{\mathrm{17}}}\right)}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\boldsymbol{{cos}}\left(\boldsymbol{{arccos}}\frac{\mathrm{4}}{\:\sqrt{\mathrm{17}}}\right)−\boldsymbol{{sin}}\left(\boldsymbol{{arcsin}}\frac{\mathrm{1}}{\:\sqrt{\mathrm{17}}}\right)\right)}\right)= \\ $$$$=\boldsymbol{{ln}}\left(\frac{\frac{\mathrm{4}}{\:\sqrt{\mathrm{17}}}}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\centerdot\frac{\mathrm{3}}{\:\sqrt{\mathrm{17}}}}\right)=\boldsymbol{{ln}}\frac{\mathrm{4}\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$
Commented by bemath last updated on 10/Oct/20
$${haha}..{same}\:{sir} \\ $$
Commented by AbduraufKodiriy last updated on 10/Oct/20
$$\left.\boldsymbol{{Yeah}}\::\right) \\ $$
Answered by Dwaipayan Shikari last updated on 10/Oct/20
![∫_(π/4) ^(π/2) ((4cosx+sinx)/(4sinx−cosx))dx =[log(4sinx−cosx)]_(π/4) ^(π/2) =2log(2)−log((3/( (√2)))) =(5/2)log(2)−log(3)](https://www.tinkutara.com/question/Q117190.png)
$$\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{4}{cosx}+{sinx}}{\mathrm{4}{sinx}−{cosx}}{dx} \\ $$$$=\left[{log}\left(\mathrm{4}{sinx}−{cosx}\right)\right]_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} =\mathrm{2}{log}\left(\mathrm{2}\right)−{log}\left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}\right) \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}}{log}\left(\mathrm{2}\right)−{log}\left(\mathrm{3}\right) \\ $$
Answered by mathmax by abdo last updated on 10/Oct/20
![A =∫_(π/4) ^(π/2) ((4cotan(x)+1)/(4−cotanx))dx ⇒ A =∫_(π/4) ^(π/2) (((4/(tanx))+1)/(4−(1/(tanx)))) dx =∫_(π/4) ^(π/2) ((4+tanx)/(4tanx−1))dx =_(tanx =t) ∫_1 ^∞ ((4+t)/(4t−1))(dt/(1+t^2 )) =∫_1 ^∞ ((t+4)/((4t−1)(t^2 +1)))dt let decompose F(t)=((t+4)/((4t−1)(t^2 +1))) F(t) =(a/(4t−1)) +((bt+c)/(t^2 +1)) a =(4t−1)F(t)∣_(t=(1/4)) =(((1/4)+4)/((1/(16))+1)) =((17)/4)×((16)/(17)) =4 lim_(t→+∞) tF(t) =0 =(a/4) +b ⇒b =−1 F(0) =−4 =−a +c ⇒c=a−4 =0 ⇒F(t)=(4/(4t−1))+((−t)/(t^2 +1)) ⇒ ∫_1 ^∞ F(t)dt =∫_1 ^∞ ((1/(t−(1/4)))−(1/2)((2t)/(t^2 +1)))dt =[ln∣((t−(1/4))/( (√(t^2 +1))))∣]_1 ^∞ =−ln∣((3/4)/( (√2)))∣ =−ln∣(3/(4(√2)))∣ =−ln(3)+ln(4(√2)) =2ln(2)+(1/2)ln2−ln(3) =(5/2)ln(2)−ln(3)](https://www.tinkutara.com/question/Q117248.png)
$$\mathrm{A}\:=\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{4cotan}\left(\mathrm{x}\right)+\mathrm{1}}{\mathrm{4}−\mathrm{cotanx}}\mathrm{dx}\:\Rightarrow\:\mathrm{A}\:=\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\frac{\mathrm{4}}{\mathrm{tanx}}+\mathrm{1}}{\mathrm{4}−\frac{\mathrm{1}}{\mathrm{tanx}}}\:\mathrm{dx} \\ $$$$=\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{4}+\mathrm{tanx}}{\mathrm{4tanx}−\mathrm{1}}\mathrm{dx}\:=_{\mathrm{tanx}\:=\mathrm{t}} \:\:\:\int_{\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{4}+\mathrm{t}}{\mathrm{4t}−\mathrm{1}}\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{t}+\mathrm{4}}{\left(\mathrm{4t}−\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)}\mathrm{dt}\:\:\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{t}+\mathrm{4}}{\left(\mathrm{4t}−\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$\mathrm{F}\left(\mathrm{t}\right)\:=\frac{\mathrm{a}}{\mathrm{4t}−\mathrm{1}}\:+\frac{\mathrm{bt}+\mathrm{c}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\mathrm{a}\:=\left(\mathrm{4t}−\mathrm{1}\right)\mathrm{F}\left(\mathrm{t}\right)\mid_{\mathrm{t}=\frac{\mathrm{1}}{\mathrm{4}}} \:\:\:\:\:=\frac{\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{4}}{\frac{\mathrm{1}}{\mathrm{16}}+\mathrm{1}}\:=\frac{\mathrm{17}}{\mathrm{4}}×\frac{\mathrm{16}}{\mathrm{17}}\:=\mathrm{4} \\ $$$$\mathrm{lim}_{\mathrm{t}\rightarrow+\infty} \mathrm{tF}\left(\mathrm{t}\right)\:=\mathrm{0}\:=\frac{\mathrm{a}}{\mathrm{4}}\:+\mathrm{b}\:\Rightarrow\mathrm{b}\:=−\mathrm{1} \\ $$$$\mathrm{F}\left(\mathrm{0}\right)\:=−\mathrm{4}\:=−\mathrm{a}\:+\mathrm{c}\:\Rightarrow\mathrm{c}=\mathrm{a}−\mathrm{4}\:=\mathrm{0}\:\Rightarrow\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{4}}{\mathrm{4t}−\mathrm{1}}+\frac{−\mathrm{t}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\int_{\mathrm{1}} ^{\infty} \mathrm{F}\left(\mathrm{t}\right)\mathrm{dt}\:=\int_{\mathrm{1}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{t}−\frac{\mathrm{1}}{\mathrm{4}}}−\frac{\mathrm{1}}{\mathrm{2}}\frac{\mathrm{2t}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\right)\mathrm{dt} \\ $$$$=\left[\mathrm{ln}\mid\frac{\mathrm{t}−\frac{\mathrm{1}}{\mathrm{4}}}{\:\sqrt{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}}\mid\right]_{\mathrm{1}} ^{\infty} \:=−\mathrm{ln}\mid\frac{\frac{\mathrm{3}}{\mathrm{4}}}{\:\sqrt{\mathrm{2}}}\mid\:=−\mathrm{ln}\mid\frac{\mathrm{3}}{\mathrm{4}\sqrt{\mathrm{2}}}\mid\:=−\mathrm{ln}\left(\mathrm{3}\right)+\mathrm{ln}\left(\mathrm{4}\sqrt{\mathrm{2}}\right) \\ $$$$=\mathrm{2ln}\left(\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln2}−\mathrm{ln}\left(\mathrm{3}\right)\:=\frac{\mathrm{5}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)−\mathrm{ln}\left(\mathrm{3}\right) \\ $$