Question Number 166263 by cortano1 last updated on 17/Feb/22
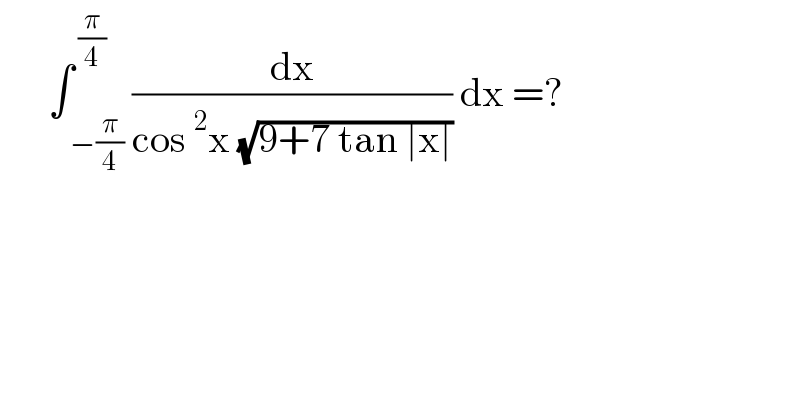
$$\:\:\:\:\:\:\int_{\:−\frac{\pi}{\mathrm{4}}} ^{\:\frac{\pi}{\mathrm{4}}} \frac{\mathrm{dx}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\:\sqrt{\mathrm{9}+\mathrm{7}\:\mathrm{tan}\:\mid\mathrm{x}\mid}}\:\mathrm{dx}\:=? \\ $$
Answered by mathsmine last updated on 17/Feb/22
![=2∫_0 ^(π/4) (dx/(cos^2 (x)(√(9+7tg(x))))) =2∫_0 ^1 (du/( (√(9+7u))))=(4/7)([(√(9+7u))]_0 ^1 ) =(4/7)](https://www.tinkutara.com/question/Q166290.png)
$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{dx}}{{cos}^{\mathrm{2}} \left({x}\right)\sqrt{\mathrm{9}+\mathrm{7}{tg}\left({x}\right)}} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{du}}{\:\sqrt{\mathrm{9}+\mathrm{7}{u}}}=\frac{\mathrm{4}}{\mathrm{7}}\left(\left[\sqrt{\mathrm{9}+\mathrm{7}{u}}\right]_{\mathrm{0}} ^{\mathrm{1}} \right) \\ $$$$=\frac{\mathrm{4}}{\mathrm{7}} \\ $$
