Question Number 95549 by Fikret last updated on 25/May/20
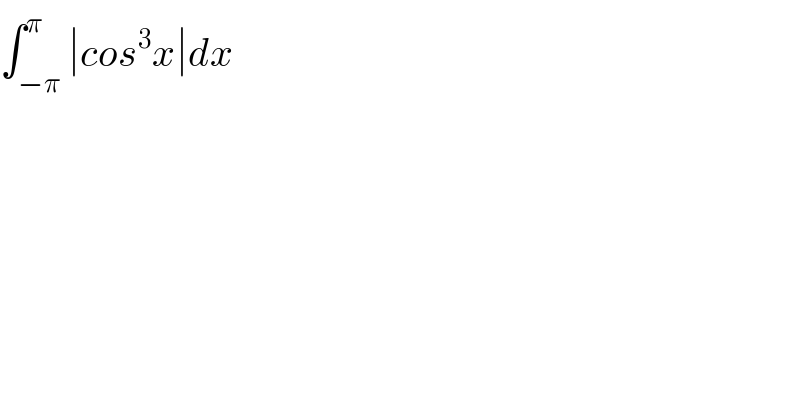
$$\int_{−\pi} ^{\pi} \mid{cos}^{\mathrm{3}} {x}\mid{dx} \\ $$
Answered by MJS last updated on 26/May/20
![∫_(−π) ^π ∣cos^3 x∣dx=4∫_0 ^(π/2) cos^3 x dx= =∫_0 ^(π/2) (cos 3x +3cos x)dx= =[(1/3)sin 3x +3sin x]_0 ^(π/2) =(8/3)](https://www.tinkutara.com/question/Q95556.png)
$$\underset{−\pi} {\overset{\pi} {\int}}\mid\mathrm{cos}^{\mathrm{3}} \:{x}\mid{dx}=\mathrm{4}\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\mathrm{cos}^{\mathrm{3}} \:{x}\:{dx}= \\ $$$$=\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\left(\mathrm{cos}\:\mathrm{3}{x}\:+\mathrm{3cos}\:{x}\right){dx}= \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}\:\mathrm{3}{x}\:+\mathrm{3sin}\:{x}\right]_{\mathrm{0}} ^{\pi/\mathrm{2}} =\frac{\mathrm{8}}{\mathrm{3}} \\ $$
Commented by peter frank last updated on 26/May/20
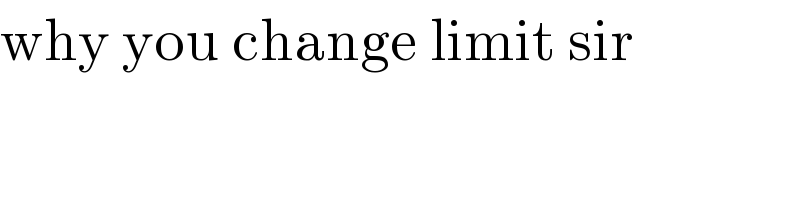
$$\mathrm{why}\:\mathrm{you}\:\mathrm{change}\:\mathrm{limit}\:\mathrm{sir} \\ $$
Commented by MJS last updated on 26/May/20
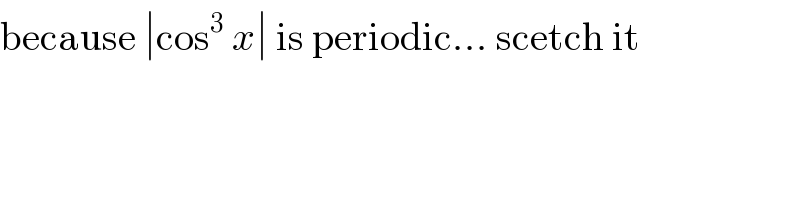
$$\mathrm{because}\:\mid\mathrm{cos}^{\mathrm{3}} \:{x}\mid\:\mathrm{is}\:\mathrm{periodic}…\:\mathrm{scetch}\:\mathrm{it} \\ $$
Commented by peter frank last updated on 26/May/20
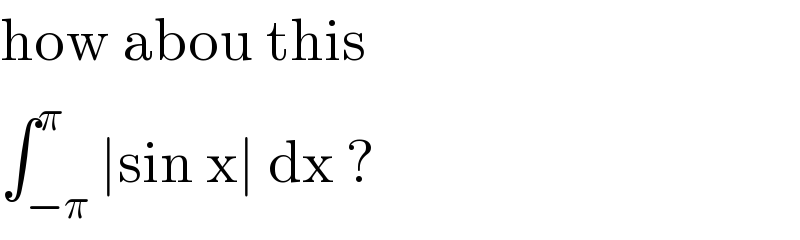
$$\mathrm{how}\:\mathrm{abou}\:\mathrm{this} \\ $$$$\int_{−\pi} ^{\pi} \mid\mathrm{sin}\:\mathrm{x}\mid\:\mathrm{dx}\:? \\ $$
Commented by MJS last updated on 26/May/20
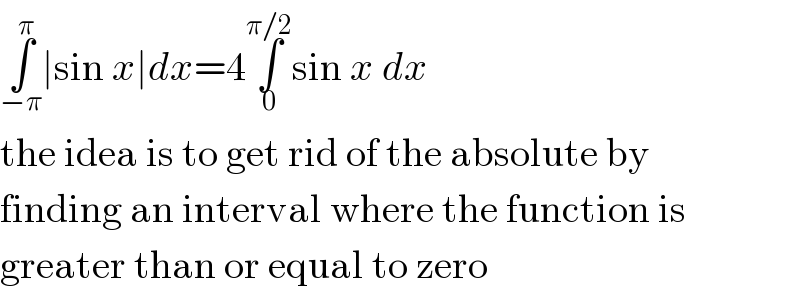
$$\underset{−\pi} {\overset{\pi} {\int}}\mid\mathrm{sin}\:{x}\mid{dx}=\mathrm{4}\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\mathrm{sin}\:{x}\:{dx} \\ $$$$\mathrm{the}\:\mathrm{idea}\:\mathrm{is}\:\mathrm{to}\:\mathrm{get}\:\mathrm{rid}\:\mathrm{of}\:\mathrm{the}\:\mathrm{absolute}\:\mathrm{by} \\ $$$$\mathrm{finding}\:\mathrm{an}\:\mathrm{interval}\:\mathrm{where}\:\mathrm{the}\:\mathrm{function}\:\mathrm{is} \\ $$$$\mathrm{greater}\:\mathrm{than}\:\mathrm{or}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{zero} \\ $$
Commented by peter frank last updated on 26/May/20

$$\mathrm{thank}\:\mathrm{you}\: \\ $$
Answered by 1549442205 last updated on 26/May/20
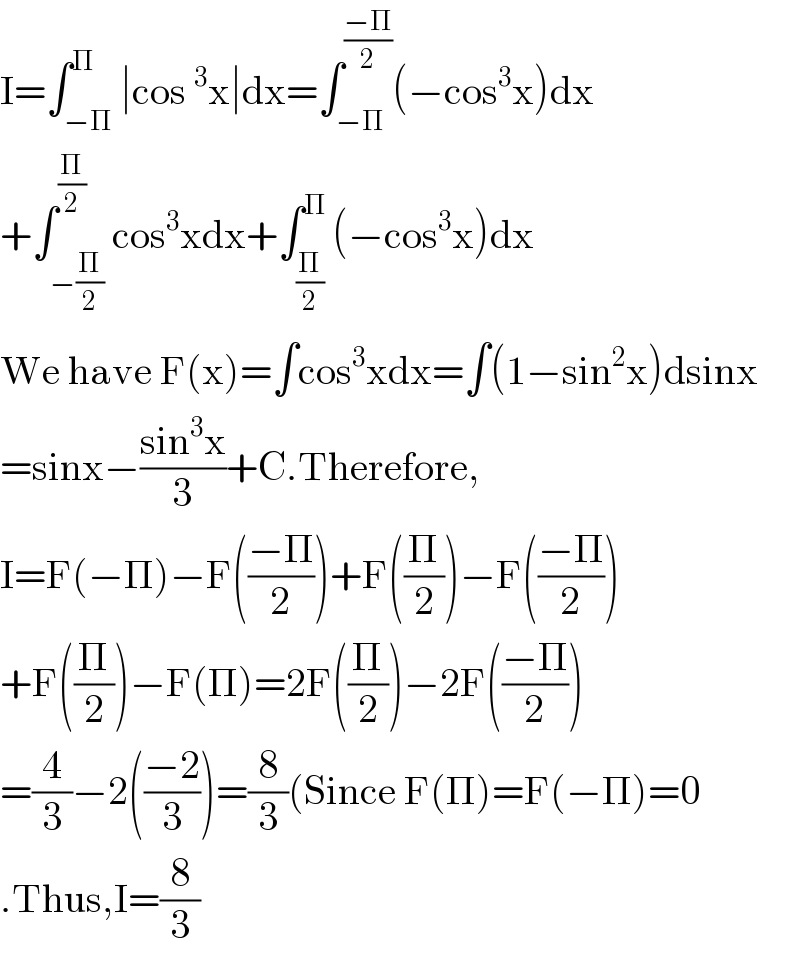
$$\mathrm{I}=\int_{−\Pi} ^{\Pi} \mid\mathrm{cos}\:^{\mathrm{3}} \mathrm{x}\mid\mathrm{dx}=\int_{−\Pi} ^{\frac{−\Pi}{\mathrm{2}}} \left(−\mathrm{cos}^{\mathrm{3}} \mathrm{x}\right)\mathrm{dx} \\ $$$$+\int_{−\frac{\Pi}{\mathrm{2}}} ^{\frac{\Pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{3}} \mathrm{xdx}+\int_{\frac{\Pi}{\mathrm{2}}} ^{\Pi} \left(−\mathrm{cos}^{\mathrm{3}} \mathrm{x}\right)\mathrm{dx} \\ $$$$\mathrm{We}\:\mathrm{have}\:\mathrm{F}\left(\mathrm{x}\right)=\int\mathrm{cos}^{\mathrm{3}} \mathrm{xdx}=\int\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)\mathrm{dsinx} \\ $$$$=\mathrm{sinx}−\frac{\mathrm{sin}^{\mathrm{3}} \mathrm{x}}{\mathrm{3}}+\mathrm{C}.\mathrm{Therefore}, \\ $$$$\mathrm{I}=\mathrm{F}\left(−\Pi\right)−\mathrm{F}\left(\frac{−\Pi}{\mathrm{2}}\right)+\mathrm{F}\left(\frac{\Pi}{\mathrm{2}}\right)−\mathrm{F}\left(\frac{−\Pi}{\mathrm{2}}\right) \\ $$$$+\mathrm{F}\left(\frac{\Pi}{\mathrm{2}}\right)−\mathrm{F}\left(\Pi\right)=\mathrm{2F}\left(\frac{\Pi}{\mathrm{2}}\right)−\mathrm{2F}\left(\frac{−\Pi}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}−\mathrm{2}\left(\frac{−\mathrm{2}}{\mathrm{3}}\right)=\frac{\mathrm{8}}{\mathrm{3}}\left(\mathrm{Since}\:\mathrm{F}\left(\Pi\right)=\mathrm{F}\left(−\Pi\right)=\mathrm{0}\right. \\ $$$$.\mathrm{Thus},\mathrm{I}=\frac{\mathrm{8}}{\mathrm{3}} \\ $$
Answered by Ar Brandon last updated on 26/May/20
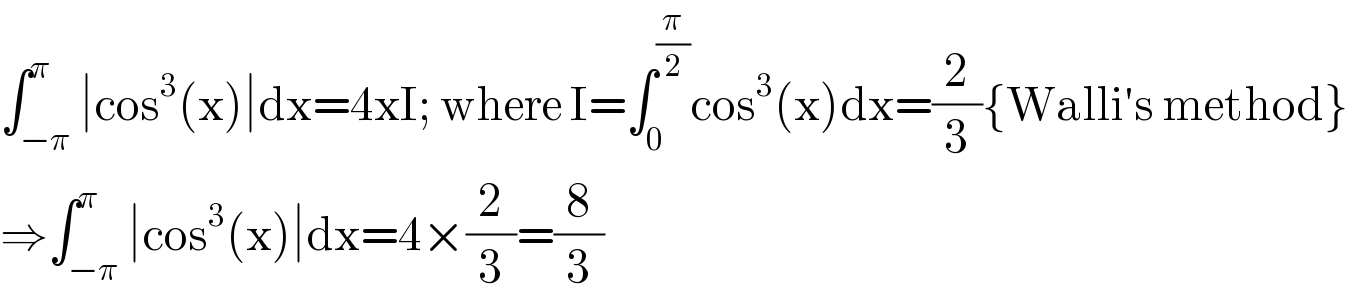
$$\int_{−\pi} ^{\pi} \mid\mathrm{cos}^{\mathrm{3}} \left(\mathrm{x}\right)\mid\mathrm{dx}=\mathrm{4xI};\:\mathrm{where}\:\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{3}} \left(\mathrm{x}\right)\mathrm{dx}=\frac{\mathrm{2}}{\mathrm{3}}\left\{\mathrm{Walli}'\mathrm{s}\:\mathrm{method}\right\} \\ $$$$\Rightarrow\int_{−\pi} ^{\pi} \mid\mathrm{cos}^{\mathrm{3}} \left(\mathrm{x}\right)\mid\mathrm{dx}=\mathrm{4}×\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{8}}{\mathrm{3}} \\ $$
