Question Number 95199 by Fikret last updated on 23/May/20
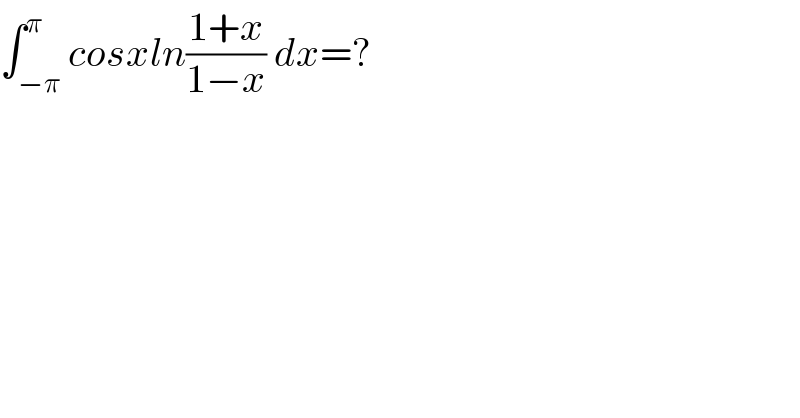
$$\int_{−\pi} ^{\pi} {cosxln}\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\:{dx}=? \\ $$
Answered by mr W last updated on 23/May/20

$${f}\left({x}\right)=\mathrm{cos}\:{x}\:\mathrm{ln}\:\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}} \\ $$$${f}\left(−{x}\right)=\mathrm{cos}\:\left(−{x}\right)\:\mathrm{ln}\:\frac{\mathrm{1}+\left(−{x}\right)}{\mathrm{1}−\left(−{x}\right)} \\ $$$$=\mathrm{cos}\:\left(−{x}\right)\:\mathrm{ln}\:\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}} \\ $$$$=\mathrm{cos}\:{x}\:\mathrm{ln}\:\left(\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\right)^{−\mathrm{1}} \\ $$$$=−\mathrm{cos}\:{x}\:\mathrm{ln}\:\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}} \\ $$$$=−{f}\left({x}\right) \\ $$$${domain}\:{of}\:{function}\:{f}\left({x}\right)\:{is}\:\left(−\mathrm{1},+\mathrm{1}\right) \\ $$$${therefore}\:\int_{−\pi} ^{\pi} {f}\left({x}\right){dx}\:{is}\:{not}\:{defined}. \\ $$$${therefore}\:{i}\:{changed}\:{it}\:{to} \\ $$$$\int_{−\pi/\mathrm{4}} ^{\pi/\mathrm{4}} {f}\left({x}\right){dx}=?. \\ $$$$ \\ $$$$\int_{−\pi/\mathrm{4}} ^{\pi/\mathrm{4}} {f}\left({x}\right){dx}=\int_{−\pi/\mathrm{4}} ^{\mathrm{0}} {f}\left({x}\right){dx}+\int_{\mathrm{0}} ^{\pi/\mathrm{4}} {f}\left({x}\right){dx} \\ $$$$=\int_{−\pi/\mathrm{4}} ^{\mathrm{0}} {f}\left(−{x}\right){d}\left(−{x}\right)+\int_{\mathrm{0}} ^{\pi/\mathrm{4}} {f}\left({x}\right){dx} \\ $$$$=\int_{\pi/\mathrm{4}} ^{\mathrm{0}} {f}\left({x}\right){dx}+\int_{\mathrm{0}} ^{\pi/\mathrm{4}} {f}\left({x}\right){dx} \\ $$$$=−\int_{\mathrm{0}} ^{\pi/\mathrm{4}} {f}\left({x}\right){dx}+\int_{\mathrm{0}} ^{\pi/\mathrm{4}} {f}\left({x}\right){dx} \\ $$$$=\mathrm{0} \\ $$
