Question Number 60881 by aliesam last updated on 26/May/19
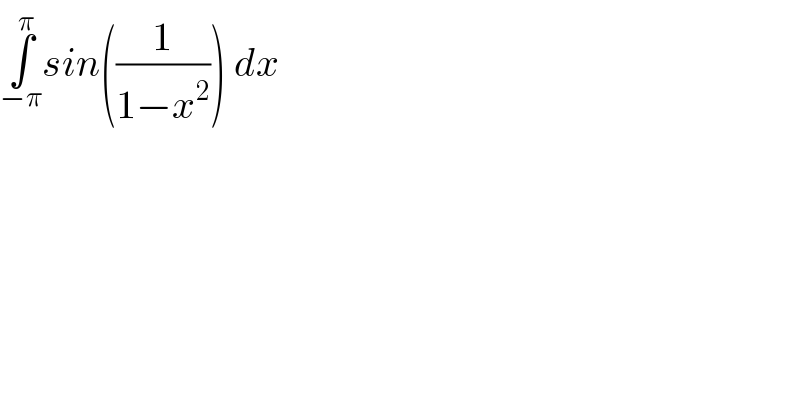
$$\underset{−\pi} {\overset{\pi} {\int}}{sin}\left(\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\right)\:{dx} \\ $$
Commented by MJS last updated on 26/May/19
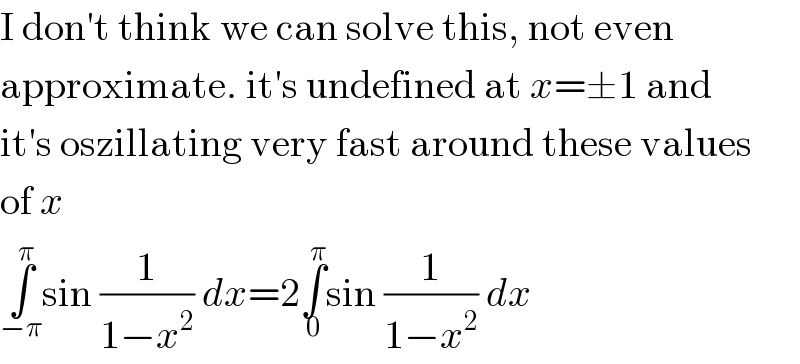
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{we}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{this},\:\mathrm{not}\:\mathrm{even} \\ $$$$\mathrm{approximate}.\:\mathrm{it}'\mathrm{s}\:\mathrm{undefined}\:\mathrm{at}\:{x}=\pm\mathrm{1}\:\mathrm{and} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{oszillating}\:\mathrm{very}\:\mathrm{fast}\:\mathrm{around}\:\mathrm{these}\:\mathrm{values} \\ $$$$\mathrm{of}\:{x} \\ $$$$\underset{−\pi} {\overset{\pi} {\int}}\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\:{dx}=\mathrm{2}\underset{\mathrm{0}} {\overset{\pi} {\int}}\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\:{dx} \\ $$
Commented by aliesam last updated on 26/May/19
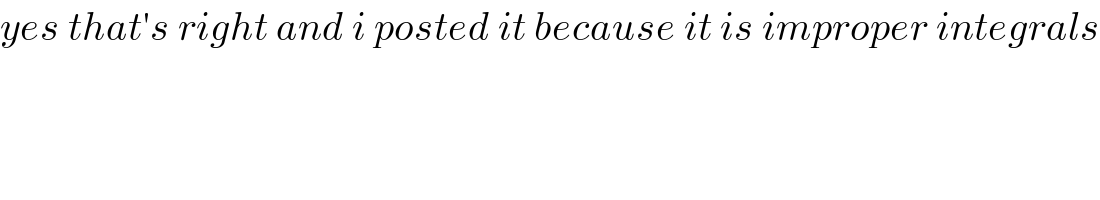
$${yes}\:{that}'{s}\:{right}\:{and}\:{i}\:{posted}\:{it}\:{because}\:{it}\:{is}\:{improper}\:{integrals} \\ $$
Commented by maxmathsup by imad last updated on 27/May/19
![let I =∫_(−π) ^π sin((1/(1−x^2 )))dx ⇒2I =∫_0 ^π sin((1/(1−x^2 )))dx =∫_0 ^1 sin((1/(1−x^2 )))dx +∫_1 ^π sin((1/(1−x^2 )))dx =H +K H =_(x =sinθ) ∫_0 ^(π/2) sin((1/(cos^2 θ)))cosθ dθ we have x−(x^3 /6) ≤sinx≤x ⇒ (1/(cos^2 θ)) −(1/(6cos^6 θ)) ≤ sin((1/(cos^2 θ))) ≤(1/(cos^2 θ)) ⇒ ∫_0 ^(π/2) cosθ sin((1/(cos^2 θ)))dθ ≥ ∫_0 ^(π/2) (dθ/(cosθ)) −(1/6) ∫_0 ^(π/2) (dθ/(cos^5 θ)) let take ∫_0 ^(π/2) (dθ/(cosθ)) ∫_0 ^(π/2) (dθ/(cosθ)) =_(tan((θ/2)) =u) ∫_0 ^1 ((2du)/((1+u^2 )((1−u^2 )/(1+u^2 )))) =∫_0 ^1 ((2du)/(1−u^2 )) =∫_0 ^1 ((1/(1+u)) +(1/(1−u)))du =[ln∣((1+u)/(1−u))∣]_0 ^1 =∞ so this integral diverge ...dont waste time to find it...!](https://www.tinkutara.com/question/Q60900.png)
$${let}\:{I}\:=\int_{−\pi} ^{\pi} \:\:{sin}\left(\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\right){dx}\:\Rightarrow\mathrm{2}{I}\:=\int_{\mathrm{0}} ^{\pi} \:{sin}\left(\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:{sin}\left(\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\right){dx}\:\:+\int_{\mathrm{1}} ^{\pi} \:{sin}\left(\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\right){dx}\:={H}\:+{K} \\ $$$${H}\:=_{{x}\:={sin}\theta} \:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}\left(\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \theta}\right){cos}\theta\:{d}\theta\:\:\:\:{we}\:{have}\:{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\:\leqslant{sinx}\leqslant{x}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \theta}\:−\frac{\mathrm{1}}{\mathrm{6}{cos}^{\mathrm{6}} \theta}\:\leqslant\:{sin}\left(\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \theta}\right)\:\leqslant\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \theta}\:\Rightarrow\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}\theta\:{sin}\left(\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \theta}\right){d}\theta\: \\ $$$$\geqslant\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{d}\theta}{{cos}\theta}\:−\frac{\mathrm{1}}{\mathrm{6}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{d}\theta}{{cos}^{\mathrm{5}} \theta}\:\:\:{let}\:{take}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{d}\theta}{{cos}\theta} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{d}\theta}{{cos}\theta}\:=_{{tan}\left(\frac{\theta}{\mathrm{2}}\right)\:={u}} \:\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{\mathrm{2}{du}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2}{du}}{\mathrm{1}−{u}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\frac{\mathrm{1}}{\mathrm{1}+{u}}\:+\frac{\mathrm{1}}{\mathrm{1}−{u}}\right){du}\:=\left[{ln}\mid\frac{\mathrm{1}+{u}}{\mathrm{1}−{u}}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\infty\:\:\:{so}\:{this}\:{integral}\:{diverge}\:\:…{dont} \\ $$$${waste}\:{time}\:{to}\:{find}\:{it}…! \\ $$
