Question Number 105393 by john santu last updated on 28/Jul/20
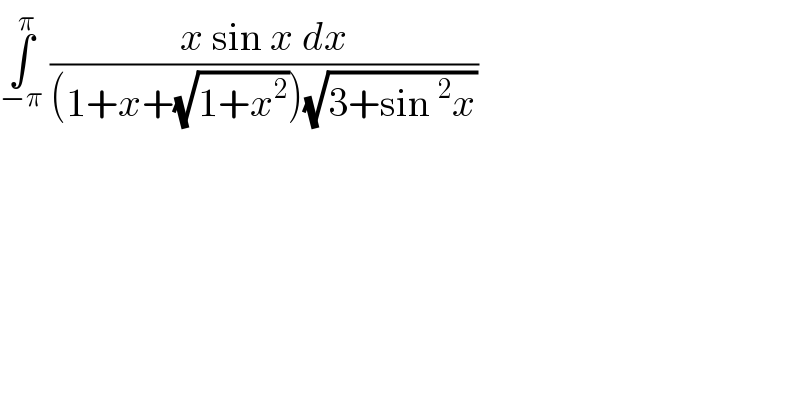
$$\underset{−\pi} {\overset{\pi} {\int}}\:\frac{{x}\:\mathrm{sin}\:{x}\:{dx}}{\left(\mathrm{1}+{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)\sqrt{\mathrm{3}+\mathrm{sin}\:^{\mathrm{2}} {x}}} \\ $$
Answered by maths mind last updated on 29/Jul/20
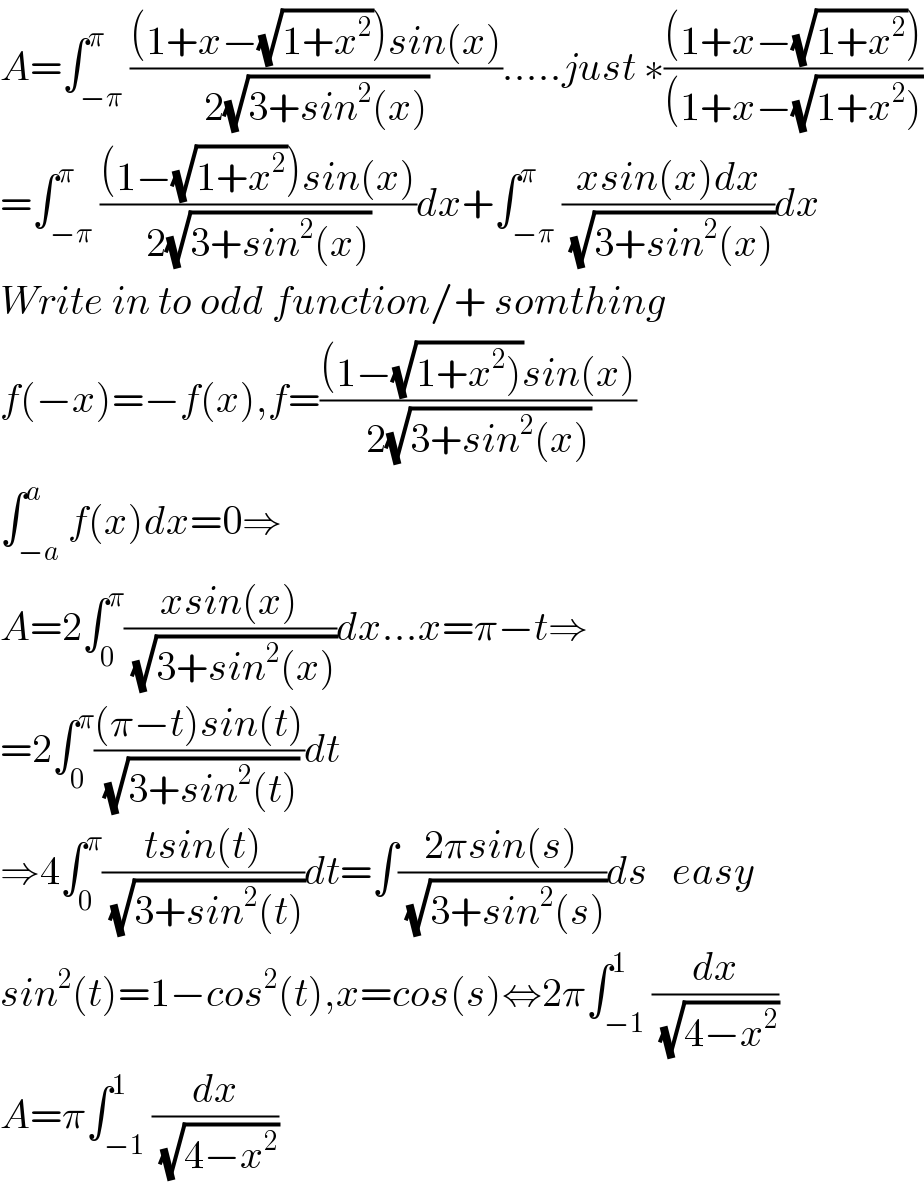
$${A}=\int_{−\pi} ^{\pi} \frac{\left(\mathrm{1}+{x}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right){sin}\left({x}\right)}{\mathrm{2}\sqrt{\mathrm{3}+{sin}^{\mathrm{2}} \left({x}\right)}}…..{just}\:\ast\frac{\left(\mathrm{1}+{x}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)}{\left(\mathrm{1}+{x}−\sqrt{\left.\mathrm{1}+{x}^{\mathrm{2}} \right)}\right.} \\ $$$$=\int_{−\pi} ^{\pi} \frac{\left(\mathrm{1}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right){sin}\left({x}\right)}{\mathrm{2}\sqrt{\mathrm{3}+{sin}^{\mathrm{2}} \left({x}\right)}}{dx}+\int_{−\pi} ^{\pi} \frac{{xsin}\left({x}\right){dx}}{\:\sqrt{\mathrm{3}+{sin}^{\mathrm{2}} \left({x}\right)}}{dx} \\ $$$${Write}\:{in}\:{to}\:{odd}\:{function}/+\:{somthing} \\ $$$${f}\left(−{x}\right)=−{f}\left({x}\right),{f}=\frac{\left(\mathrm{1}−\sqrt{\left.\mathrm{1}+{x}^{\mathrm{2}} \right)}{sin}\left({x}\right)\right.}{\mathrm{2}\sqrt{\mathrm{3}+{sin}^{\mathrm{2}} \left({x}\right)}} \\ $$$$\int_{−{a}} ^{{a}} {f}\left({x}\right){dx}=\mathrm{0}\Rightarrow \\ $$$${A}=\mathrm{2}\int_{\mathrm{0}} ^{\pi} \frac{{xsin}\left({x}\right)}{\:\sqrt{\mathrm{3}+{sin}^{\mathrm{2}} \left({x}\right)}}{dx}…{x}=\pi−{t}\Rightarrow \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\pi} \frac{\left(\pi−{t}\right){sin}\left({t}\right)}{\:\sqrt{\mathrm{3}+{sin}^{\mathrm{2}} \left({t}\right)}}{dt} \\ $$$$\Rightarrow\mathrm{4}\int_{\mathrm{0}} ^{\pi} \frac{{tsin}\left({t}\right)}{\:\sqrt{\mathrm{3}+{sin}^{\mathrm{2}} \left({t}\right)}}{dt}=\int\frac{\mathrm{2}\pi{sin}\left({s}\right)}{\:\sqrt{\mathrm{3}+{sin}^{\mathrm{2}} \left({s}\right)}}{ds}\:\:\:{easy} \\ $$$${sin}^{\mathrm{2}} \left({t}\right)=\mathrm{1}−{cos}^{\mathrm{2}} \left({t}\right),{x}={cos}\left({s}\right)\Leftrightarrow\mathrm{2}\pi\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{{dx}}{\:\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }} \\ $$$${A}=\pi\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{{dx}}{\:\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }} \\ $$
