Menu Close

pleas-solve-this-1-lim-x-1-e-x-2x-3x-4x-nx-e-n-n-1-2-x-1-2-lim-x-1-e-2-x-3-x-4-x-n-x-e-n-x-1-3-lim-x-1-e-x-x-2-x-3-x-n-e-n-x

Tinku Tara 0 Comments
Pin




Question Number 189145 by mathlove last updated on 12/Mar/23
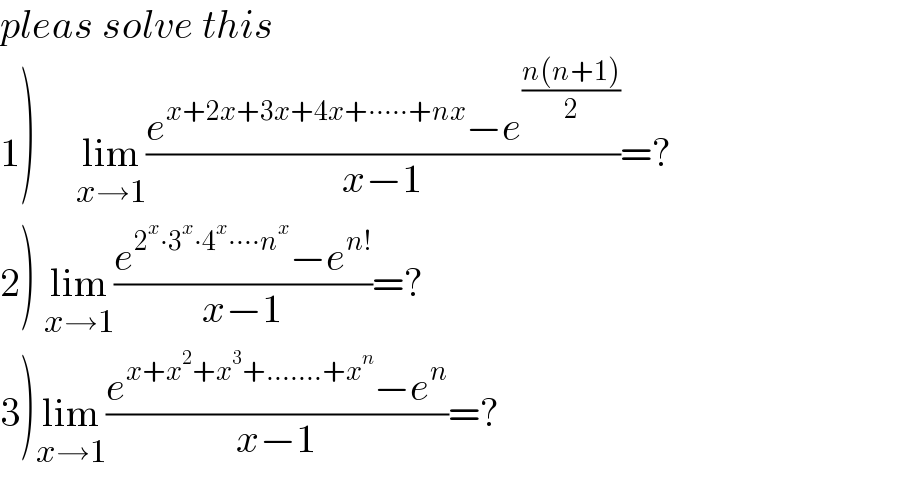
pleas solve this 1) lim_(x→1) ((e^(x+2x+3x+4x+∙∙∙∙∙+nx) −e^((n(n+1))/2) )/(x−1))=? 2) lim_(x→1) ((e^(2^x ∙3^x ∙4^x ∙∙∙∙n^x ) −e^(n!) )/(x−1))=? 3)lim_(x→1) ((e^(x+x^2 +x^3 +.......+x^n ) −e^n )/(x−1))=?
$${pleas}\:{solve}\:{this} \\ $$$$\left.\mathrm{1}\right)\:\:\:\:\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{e}^{{x}+\mathrm{2}{x}+\mathrm{3}{x}+\mathrm{4}{x}+\centerdot\centerdot\centerdot\centerdot\centerdot+{nx}} −{e}^{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}} }{{x}−\mathrm{1}}=? \\ $$$$\left.\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{e}^{\mathrm{2}^{{x}} \centerdot\mathrm{3}^{{x}} \centerdot\mathrm{4}^{{x}} \centerdot\centerdot\centerdot\centerdot{n}^{{x}} } −{e}^{{n}!} }{{x}−\mathrm{1}}=? \\ $$$$\left.\mathrm{3}\right)\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{e}^{{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…….+{x}^{{n}} } −{e}^{{n}} }{{x}−\mathrm{1}}=? \\ $$
Answered by Ar Brandon last updated on 12/Mar/23
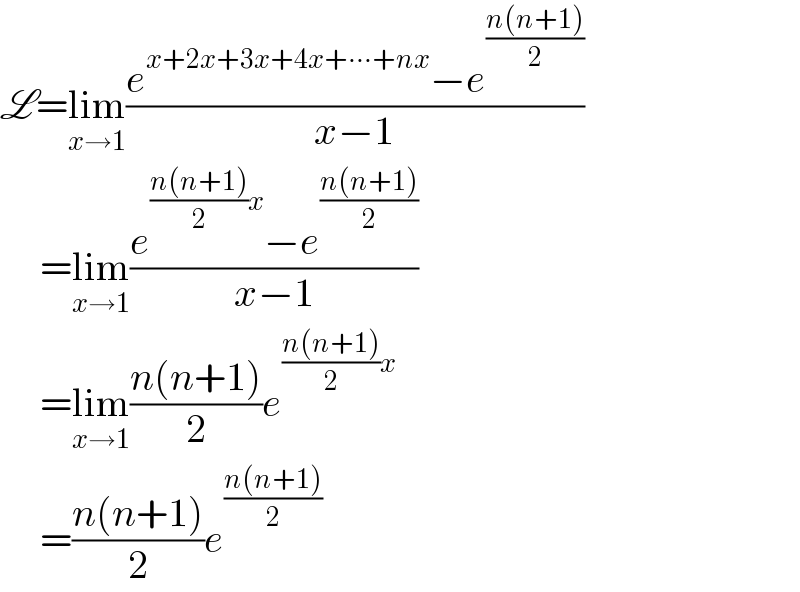
L=lim_(x→1) ((e^(x+2x+3x+4x+∙∙∙+nx) −e^((n(n+1))/2) )/(x−1)) =lim_(x→1) ((e^(((n(n+1))/2)x) −e^((n(n+1))/2) )/(x−1)) =lim_(x→1) ((n(n+1))/2)e^(((n(n+1))/2)x) =((n(n+1))/2)e^((n(n+1))/2)
$$\mathscr{L}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{e}^{{x}+\mathrm{2}{x}+\mathrm{3}{x}+\mathrm{4}{x}+\centerdot\centerdot\centerdot+{nx}} −{e}^{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}} }{{x}−\mathrm{1}} \\ $$$$\:\:\:\:\:=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{e}^{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}{x}} −{e}^{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}} }{{x}−\mathrm{1}} \\ $$$$\:\:\:\:\:=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}{e}^{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}{x}} \\ $$$$\:\:\:\:\:=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}{e}^{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}} \\ $$
Answered by Ar Brandon last updated on 12/Mar/23
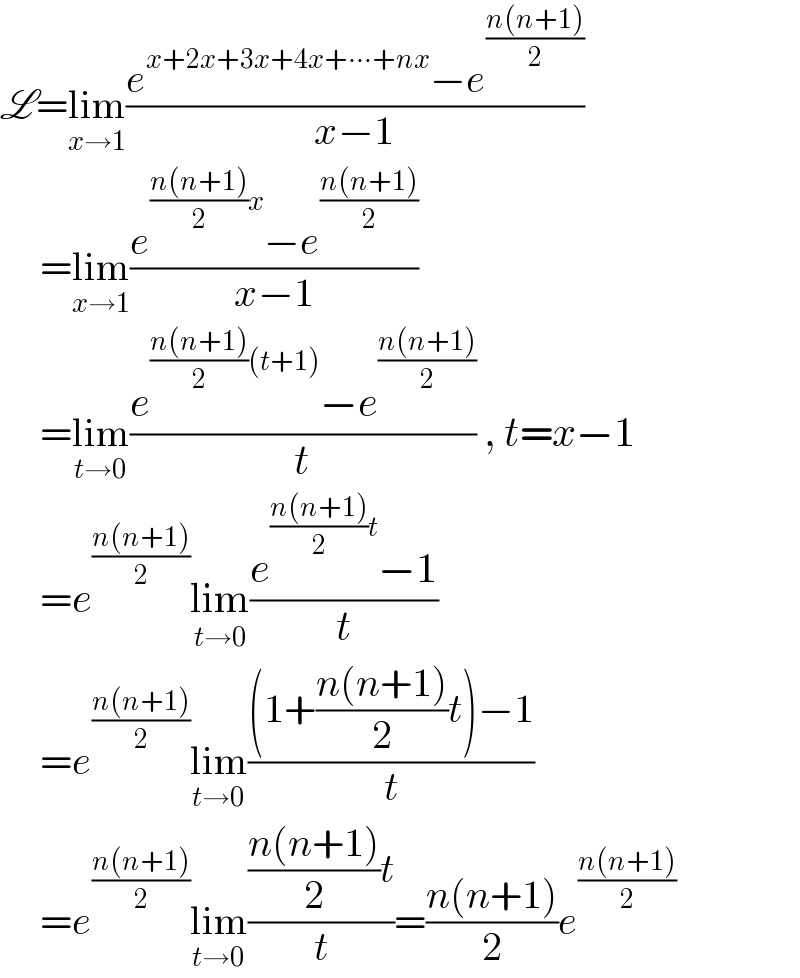
L=lim_(x→1) ((e^(x+2x+3x+4x+∙∙∙+nx) −e^((n(n+1))/2) )/(x−1)) =lim_(x→1) ((e^(((n(n+1))/2)x) −e^((n(n+1))/2) )/(x−1)) =lim_(t→0) ((e^(((n(n+1))/2)(t+1)) −e^((n(n+1))/2) )/t) , t=x−1 =e^((n(n+1))/2) lim_(t→0) ((e^(((n(n+1))/2)t) −1)/t) =e^((n(n+1))/2) lim_(t→0) (((1+((n(n+1))/2)t)−1)/t) =e^((n(n+1))/2) lim_(t→0) ((((n(n+1))/2)t)/t)=((n(n+1))/2)e^((n(n+1))/2)
$$\mathscr{L}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{e}^{{x}+\mathrm{2}{x}+\mathrm{3}{x}+\mathrm{4}{x}+\centerdot\centerdot\centerdot+{nx}} −{e}^{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}} }{{x}−\mathrm{1}} \\ $$$$\:\:\:\:\:=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{e}^{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}{x}} −{e}^{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}} }{{x}−\mathrm{1}} \\ $$$$\:\:\:\:\:=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\left({t}+\mathrm{1}\right)} −{e}^{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}} }{{t}}\:,\:{t}={x}−\mathrm{1} \\ $$$$\:\:\:\:\:={e}^{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}} \underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}{t}} −\mathrm{1}}{{t}} \\ $$$$\:\:\:\:\:={e}^{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}} \underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{1}+\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}{t}\right)−\mathrm{1}}{{t}} \\ $$$$\:\:\:\:\:={e}^{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}} \underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}{t}}{{t}}=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}{e}^{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}} \\ $$
Answered by CElcedricjunior last updated on 15/Mar/23
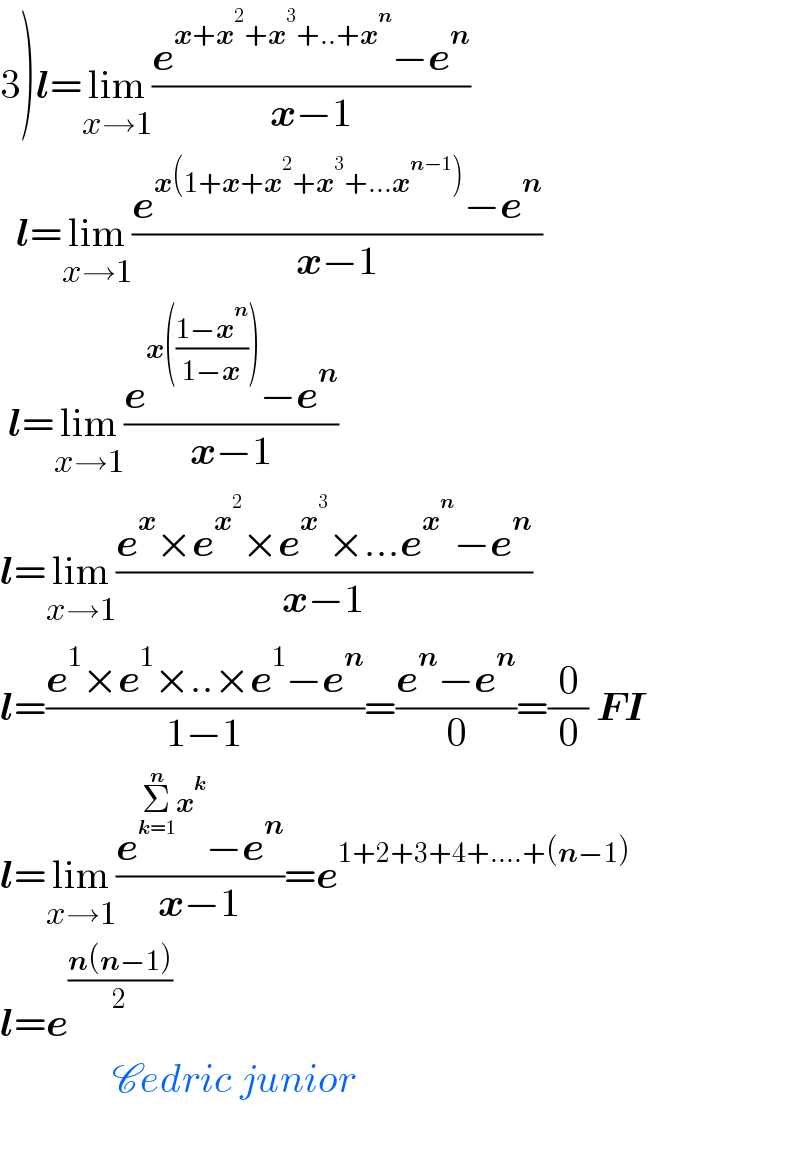
3)l=lim_(x→1) ((e^(x+x^2 +x^3 +..+x^n ) −e^n )/(x−1)) l=lim_(x→1) ((e^(x(1+x+x^2 +x^3 +...x^(n−1) )) −e^n )/(x−1)) l=lim_(x→1) ((e^(x(((1−x^n )/(1−x)))) −e^n )/(x−1)) l=lim_(x→1) ((e^x ×e^x^2 ×e^x^3 ×...e^x^n −e^n )/(x−1)) l=((e^1 ×e^1 ×..×e^1 −e^n )/(1−1))=((e^n −e^n )/0)=(0/0) FI l=lim_(x→1) ((e^(Σ_(k=1) ^n x^k ) −e^n )/(x−1))=e^(1+2+3+4+....+(n−1)) l=e^((n(n−1))/2) Cedric junior
$$\left.\mathrm{3}\right)\boldsymbol{{l}}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\boldsymbol{{e}}^{\boldsymbol{{x}}+\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{x}}^{\mathrm{3}} +..+\boldsymbol{{x}}^{\boldsymbol{{n}}} } −\boldsymbol{{e}}^{\boldsymbol{{n}}} }{\boldsymbol{{x}}−\mathrm{1}} \\ $$$$\:\:\boldsymbol{{l}}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\boldsymbol{{e}}^{\boldsymbol{{x}}\left(\mathrm{1}+\boldsymbol{{x}}+\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{x}}^{\mathrm{3}} +…\boldsymbol{{x}}^{\boldsymbol{{n}}−\mathrm{1}} \right)} −\boldsymbol{{e}}^{\boldsymbol{{n}}} }{\boldsymbol{{x}}−\mathrm{1}} \\ $$$$\:\boldsymbol{{l}}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\boldsymbol{{e}}^{\boldsymbol{{x}}\left(\frac{\mathrm{1}−\boldsymbol{{x}}^{\boldsymbol{{n}}} }{\mathrm{1}−\boldsymbol{{x}}}\right)} −\boldsymbol{{e}}^{\boldsymbol{{n}}} }{\boldsymbol{{x}}−\mathrm{1}} \\ $$$$\boldsymbol{{l}}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\boldsymbol{{e}}^{\boldsymbol{{x}}} ×\boldsymbol{{e}}^{\boldsymbol{{x}}^{\mathrm{2}} } ×\boldsymbol{{e}}^{\boldsymbol{{x}}^{\mathrm{3}} } ×…\boldsymbol{{e}}^{\boldsymbol{{x}}^{\boldsymbol{{n}}} } −\boldsymbol{{e}}^{\boldsymbol{{n}}} }{\boldsymbol{{x}}−\mathrm{1}} \\ $$$$\boldsymbol{{l}}=\frac{\boldsymbol{{e}}^{\mathrm{1}} ×\boldsymbol{{e}}^{\mathrm{1}} ×..×\boldsymbol{{e}}^{\mathrm{1}} −\boldsymbol{{e}}^{\boldsymbol{{n}}} }{\mathrm{1}−\mathrm{1}}=\frac{\boldsymbol{{e}}^{\boldsymbol{{n}}} −\boldsymbol{{e}}^{\boldsymbol{{n}}} }{\mathrm{0}}=\frac{\mathrm{0}}{\mathrm{0}}\:\boldsymbol{{FI}} \\ $$$$\boldsymbol{{l}}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\boldsymbol{{e}}^{\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\sum}}\boldsymbol{{x}}^{\boldsymbol{{k}}} } −\boldsymbol{{e}}^{\boldsymbol{{n}}} }{\boldsymbol{{x}}−\mathrm{1}}=\boldsymbol{{e}}^{\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+….+\left(\boldsymbol{{n}}−\mathrm{1}\right)} \\ $$$$\boldsymbol{{l}}=\boldsymbol{{e}}^{\frac{\boldsymbol{{n}}\left(\boldsymbol{{n}}−\mathrm{1}\right)}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathscr{C}{edric}\:{junior}\: \\ $$$$ \\ $$
Answered by CElcedricjunior last updated on 14/Mar/23
1)l=lim_(x→1) ((e^(x+2x+3x+4x+...+nx) −e^((n(n+1))/2) )/(x−1)) =lim_(x→1) ((e^(x(1+2+....+n)) −e^((n(n+1))/2) )/(x−1)) =lim_(x→1) ((e^(((n(n+1))/2)x) −e^((n(n+1))/2) )/(x−1))=lim_(x→1) ((f_n (x)−f_n (1))/(x−1)) =[f_n ′(1)] avec f_n (x)=e^(((n(n+1))/2)x) =((n(n+1))/2)e^((n(n+1))/2)
$$\left.\mathrm{1}\right){l}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\boldsymbol{{e}}^{\boldsymbol{{x}}+\mathrm{2}\boldsymbol{{x}}+\mathrm{3}\boldsymbol{{x}}+\mathrm{4}\boldsymbol{{x}}+…+\boldsymbol{{nx}}} −\boldsymbol{{e}}^{\frac{\boldsymbol{{n}}\left(\boldsymbol{{n}}+\mathrm{1}\right)}{\mathrm{2}}} }{\boldsymbol{{x}}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\boldsymbol{{e}}^{\boldsymbol{{x}}\left(\mathrm{1}+\mathrm{2}+….+\boldsymbol{{n}}\right)} −\boldsymbol{{e}}^{\frac{\boldsymbol{{n}}\left(\boldsymbol{{n}}+\mathrm{1}\right)}{\mathrm{2}}} }{\boldsymbol{{x}}−\mathrm{1}} \\ $$$$\:\:\:\:\:=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\boldsymbol{{e}}^{\frac{\boldsymbol{{n}}\left(\boldsymbol{{n}}+\mathrm{1}\right)}{\mathrm{2}}\boldsymbol{{x}}} −\boldsymbol{{e}}^{\frac{\boldsymbol{{n}}\left(\boldsymbol{{n}}+\mathrm{1}\right)}{\mathrm{2}}} }{\boldsymbol{{x}}−\mathrm{1}}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\boldsymbol{{f}}_{\boldsymbol{{n}}} \left(\boldsymbol{{x}}\right)−\boldsymbol{{f}}_{\boldsymbol{{n}}} \left(\mathrm{1}\right)}{\boldsymbol{{x}}−\mathrm{1}} \\ $$$$=\left[\boldsymbol{{f}}_{{n}} '\left(\mathrm{1}\right)\right]\:\boldsymbol{{avec}}\:\boldsymbol{{f}}_{\boldsymbol{{n}}} \left(\boldsymbol{{x}}\right)=\boldsymbol{{e}}^{\frac{\boldsymbol{{n}}\left(\boldsymbol{{n}}+\mathrm{1}\right)}{\mathrm{2}}\boldsymbol{{x}}} \\ $$$$=\frac{\boldsymbol{{n}}\left(\boldsymbol{{n}}+\mathrm{1}\right)}{\mathrm{2}}\boldsymbol{{e}}^{\frac{\boldsymbol{{n}}\left(\boldsymbol{{n}}+\mathrm{1}\right)}{\mathrm{2}}} \\ $$$$ \\ $$
Answered by CElcedricjunior last updated on 14/Mar/23
2)l=lim_(x→1) ((e^(2^x .3^x ....n^x ) −e^(n!) )/(x−1)) l=lim_(x→1) ((e^(Π_(k=1) ^n (k)^x ) −e^(n!) )/(x−1)) l=lim_(x→1) ((e^((n!)^x ) −e^(n!) )/(x−1))=lim_(x→1) ((g_n (x)−g_n (1))/(x−1)) avec g_n (x)=e^((n!)^x ) l=g_n ′(1)=ln(n!)n! e^(n!)
$$\left.\mathrm{2}\right)\boldsymbol{{l}}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\boldsymbol{{e}}^{\mathrm{2}^{\boldsymbol{{x}}} .\mathrm{3}^{\boldsymbol{{x}}} ….\boldsymbol{{n}}^{\boldsymbol{{x}}} } −\boldsymbol{{e}}^{\boldsymbol{{n}}!} }{\boldsymbol{{x}}−\mathrm{1}} \\ $$$$\:\:\:\boldsymbol{{l}}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\boldsymbol{{e}}^{\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\prod}}\left(\boldsymbol{{k}}\right)^{\boldsymbol{{x}}} } −\boldsymbol{{e}}^{\boldsymbol{{n}}!} }{\boldsymbol{{x}}−\mathrm{1}} \\ $$$$\:\:\boldsymbol{{l}}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\boldsymbol{{e}}^{\left(\boldsymbol{{n}}!\right)^{\boldsymbol{{x}}} } −\boldsymbol{{e}}^{\boldsymbol{{n}}!} }{\boldsymbol{{x}}−\mathrm{1}}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\boldsymbol{{g}}_{\boldsymbol{{n}}} \left(\boldsymbol{{x}}\right)−\boldsymbol{{g}}_{\boldsymbol{{n}}} \left(\mathrm{1}\right)}{\boldsymbol{{x}}−\mathrm{1}} \\ $$$$\boldsymbol{{avec}}\:\:\boldsymbol{{g}}_{\boldsymbol{{n}}} \left(\boldsymbol{{x}}\right)=\boldsymbol{{e}}^{\left(\boldsymbol{{n}}!\right)^{\boldsymbol{{x}}} } \\ $$$$\:\:\:\boldsymbol{{l}}=\boldsymbol{{g}}_{\boldsymbol{{n}}} '\left(\mathrm{1}\right)=\boldsymbol{{ln}}\left(\boldsymbol{{n}}!\right){n}!\:\boldsymbol{{e}}^{\boldsymbol{{n}}!} \\ $$
Answered by TUN last updated on 14/Mar/23
3)lim_(x→1) ((e^(x+x^2 +x^3 +...+x^n ) −e^n )/(x−1))=lim_(x→1) ((e^(x.((x^n −1)/(x−1))) −e^n )/(x−1)) =lim_(x→1) ((e^(x.(x^(n−1) +x^(n−2) +...+x^1 +1)) −e^n )/(x−1)) =lim_(x→1) ((e^((x^n +x^(n−1) +...+x^2 +x)) −e^n )/(x−1))=lim_(x→1) [nx^(n−1) +(n−1)x^(n−2) +...+2x+1]e^((x^n +x^(n−1) +...+x^2 +x)) =lim_(x→1) (n+n−1+n−2+...+2+1)e^n =[n+((n(n−1))/2)].e^n =((n(n+1))/2).e^n
$$ \\ $$$$\left.\mathrm{3}\right)\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{e}^{{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…+{x}^{{n}} } −{e}^{{n}} }{{x}−\mathrm{1}}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{e}^{{x}.\frac{{x}^{{n}} −\mathrm{1}}{{x}−\mathrm{1}}} −{e}^{{n}} }{{x}−\mathrm{1}} \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{e}^{{x}.\left({x}^{{n}−\mathrm{1}} +{x}^{{n}−\mathrm{2}} +…+{x}^{\mathrm{1}} +\mathrm{1}\right)} −{e}^{{n}} }{{x}−\mathrm{1}} \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{e}^{\left({x}^{{n}} +{x}^{{n}−\mathrm{1}} +…+{x}^{\mathrm{2}} +{x}\right)} −{e}^{{n}} }{{x}−\mathrm{1}}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left[{nx}^{{n}−\mathrm{1}} +\left({n}−\mathrm{1}\right){x}^{{n}−\mathrm{2}} +…+\mathrm{2}{x}+\mathrm{1}\right]{e}^{\left({x}^{{n}} +{x}^{{n}−\mathrm{1}} +…+{x}^{\mathrm{2}} +{x}\right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left({n}+{n}−\mathrm{1}+{n}−\mathrm{2}+…+\mathrm{2}+\mathrm{1}\right){e}^{{n}} =\left[{n}+\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}\right].{e}^{{n}} \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}.{e}^{{n}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *