Question Number 156009 by zainaltanjung last updated on 07/Oct/21
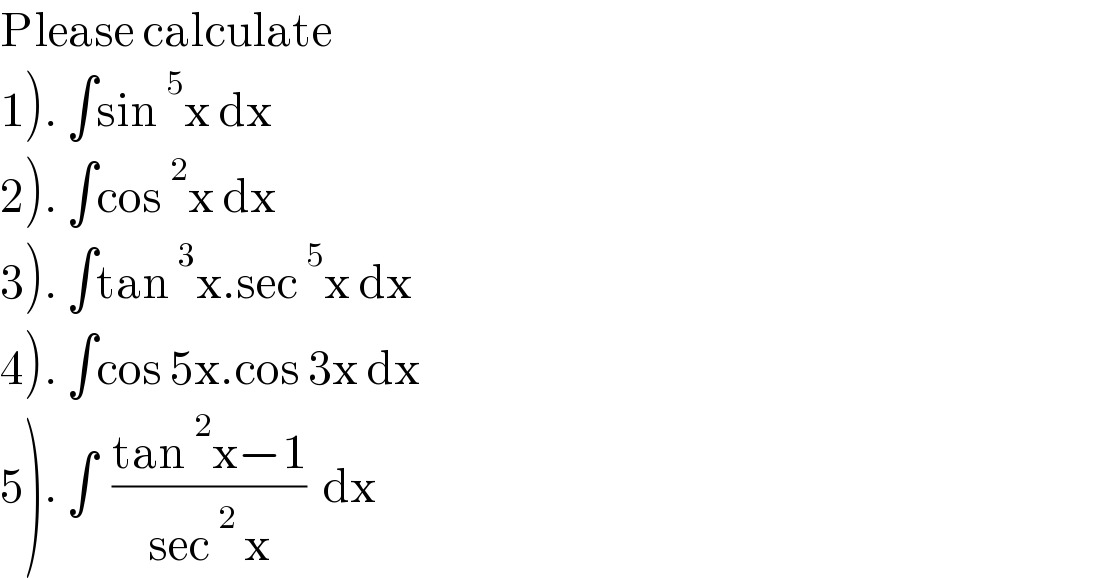
$$\mathrm{Please}\:\mathrm{calculate} \\ $$$$\left.\mathrm{1}\right).\:\int\mathrm{sin}\:^{\mathrm{5}} \mathrm{x}\:\mathrm{dx} \\ $$$$\left.\mathrm{2}\right).\:\int\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{dx} \\ $$$$\left.\mathrm{3}\right).\:\int\mathrm{tan}\:^{\mathrm{3}} \mathrm{x}.\mathrm{sec}\:^{\mathrm{5}} \mathrm{x}\:\mathrm{dx} \\ $$$$\left.\mathrm{4}\right).\:\int\mathrm{cos}\:\mathrm{5x}.\mathrm{cos}\:\mathrm{3x}\:\mathrm{dx} \\ $$$$\left.\mathrm{5}\right).\:\int\:\:\frac{\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}−\mathrm{1}}{\mathrm{sec}\:^{\mathrm{2}} \:\mathrm{x}}\:\:\mathrm{dx} \\ $$
Commented by aliyn last updated on 07/Oct/21

$$\left.\mathrm{5}\:\right)\:\int\:\frac{{tan}^{\mathrm{2}} {x}\:−\:\mathrm{1}}{{sec}^{\mathrm{2}} {x}}\:{dx}\:\:=\:\int\:\:\frac{{sec}^{\mathrm{2}} {x}\:−\:\mathrm{2}}{{sec}^{\mathrm{2}} {x}}\:{dx} \\ $$$$ \\ $$$$=\:{x}\:−\:\int\:\left(\:\mathrm{1}\:+\:{cos}\mathrm{2}{x}\:\right)\:{dx}=\:{x}\:−\:{x}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\:{sin}\mathrm{2}{x}\:+\:{c}\: \\ $$$$ \\ $$$$=\:−\:{sinx}\:{cosx}\:+\:{c}\: \\ $$$$ \\ $$$$\circledast\:\boldsymbol{{M}} \\ $$
Commented by aliyn last updated on 07/Oct/21

$$\left.\mathrm{2}\right)\:\int\:{cos}^{\mathrm{2}} {x}\:{dx}\:=\:\int\:\frac{\mathrm{1}}{\mathrm{2}}\:\left(\:\mathrm{1}\:+\:{cos}\mathrm{2}{x}\right)\:{dx}\: \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}{x}\:+\:\frac{\mathrm{1}}{\mathrm{2}}{sinx}\:{cosx}\:+\:{c} \\ $$$$ \\ $$$$\circledast\boldsymbol{{M}} \\ $$
Commented by aliyn last updated on 07/Oct/21
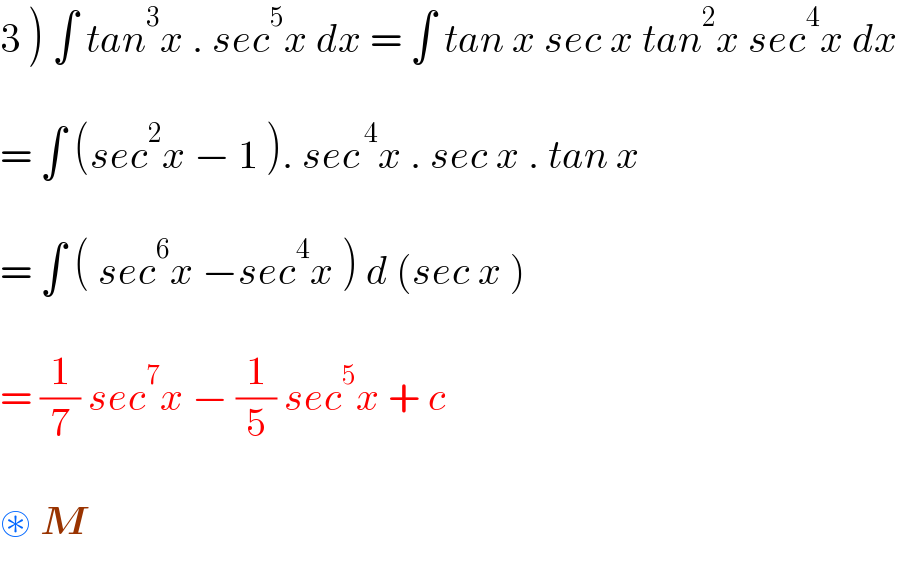
$$\left.\mathrm{3}\:\right)\:\int\:{tan}^{\mathrm{3}} {x}\:.\:{sec}^{\mathrm{5}} {x}\:{dx}\:=\:\int\:{tan}\:{x}\:{sec}\:{x}\:{tan}^{\mathrm{2}} {x}\:{sec}^{\mathrm{4}} {x}\:{dx} \\ $$$$ \\ $$$$=\:\int\:\left({sec}^{\mathrm{2}} {x}\:−\:\mathrm{1}\:\right).\:{sec}^{\:\mathrm{4}} {x}\:.\:{sec}\:{x}\:.\:{tan}\:{x}\: \\ $$$$ \\ $$$$=\:\int\:\left(\:{sec}^{\mathrm{6}} {x}\:−{sec}^{\mathrm{4}} {x}\:\right)\:{d}\:\left({sec}\:{x}\:\right) \\ $$$$ \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{7}}\:{sec}^{\mathrm{7}} {x}\:−\:\frac{\mathrm{1}}{\mathrm{5}}\:{sec}^{\mathrm{5}} {x}\:+\:{c} \\ $$$$ \\ $$$$\circledast\:\boldsymbol{{M}} \\ $$
Commented by aliyn last updated on 07/Oct/21

$$\left.\mathrm{4}\:\right)\:\int\:{cos}\:\mathrm{5}{x}\:.\:{cos}\:\mathrm{3}{x}\:{dx}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\left({cos}\:\mathrm{8}{x}\:+\:{cos}\:\mathrm{2}{x}\:\right){dx} \\ $$$$ \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{16}}\:{sin}\mathrm{8}{x}\:+\:\frac{\mathrm{1}}{\mathrm{4}}\:{sin}\mathrm{2}{x}\:+\:{c} \\ $$$$ \\ $$$$\square\:\boldsymbol{{M}} \\ $$
Commented by aliyn last updated on 07/Oct/21

$$\left.\mathrm{1}\:\right)\:\int\:\:{sin}^{\mathrm{5}} {x}\:{dx}\:=\:\int\:\left(\:{sin}^{\mathrm{2}} {x}\:\right)\:^{\mathrm{2}} \:{sin}\:{x}\:{dx}\: \\ $$$$ \\ $$$$=\:\int\:\left(\:\mathrm{1}\:−\:{cos}^{\mathrm{2}} {x}\:\right)^{\mathrm{2}} \:{sin}\:{x}\:{dx} \\ $$$$ \\ $$$$=\:\:\int\:\left(\:\mathrm{1}\:−\:\mathrm{2}\:{cos}^{\mathrm{2}} {x}\:+\:{cos}^{\mathrm{4}} {x}\:\right)\:{sin}\:{x}\:{dx} \\ $$$$ \\ $$$$=\:\int\:\left(\:{sinx}\:−\:\mathrm{2}\:{sin}\:{x}\:{cos}^{\mathrm{2}} {x}\:+\:{sin}\:{x}\:{cos}^{\mathrm{4}} {x}\:\right)\:{dx} \\ $$$$ \\ $$$$=\:−\:{cos}\:{x}\:+\:\frac{\mathrm{2}}{\mathrm{3}}\:{cos}^{\mathrm{3}} {x}\:−\:\frac{\mathrm{1}}{\mathrm{5}}\:{cos}^{\mathrm{5}} {x}\:+\:{c} \\ $$$$ \\ $$$$\oplus\:\boldsymbol{{M}} \\ $$
