Menu Close

please-calculate-A-and-B-A-1-1-4-1-1-9-1-1-16-1-1-4-084-441-and-2021-2-4084441-B-1-2-2-2-3-2-4-2-5-2-6-2-7-2-8-2-9-2-10-2-11-2-

Tinku Tara 0 Comments
Pin




Question Number 161377 by stelor last updated on 17/Dec/21
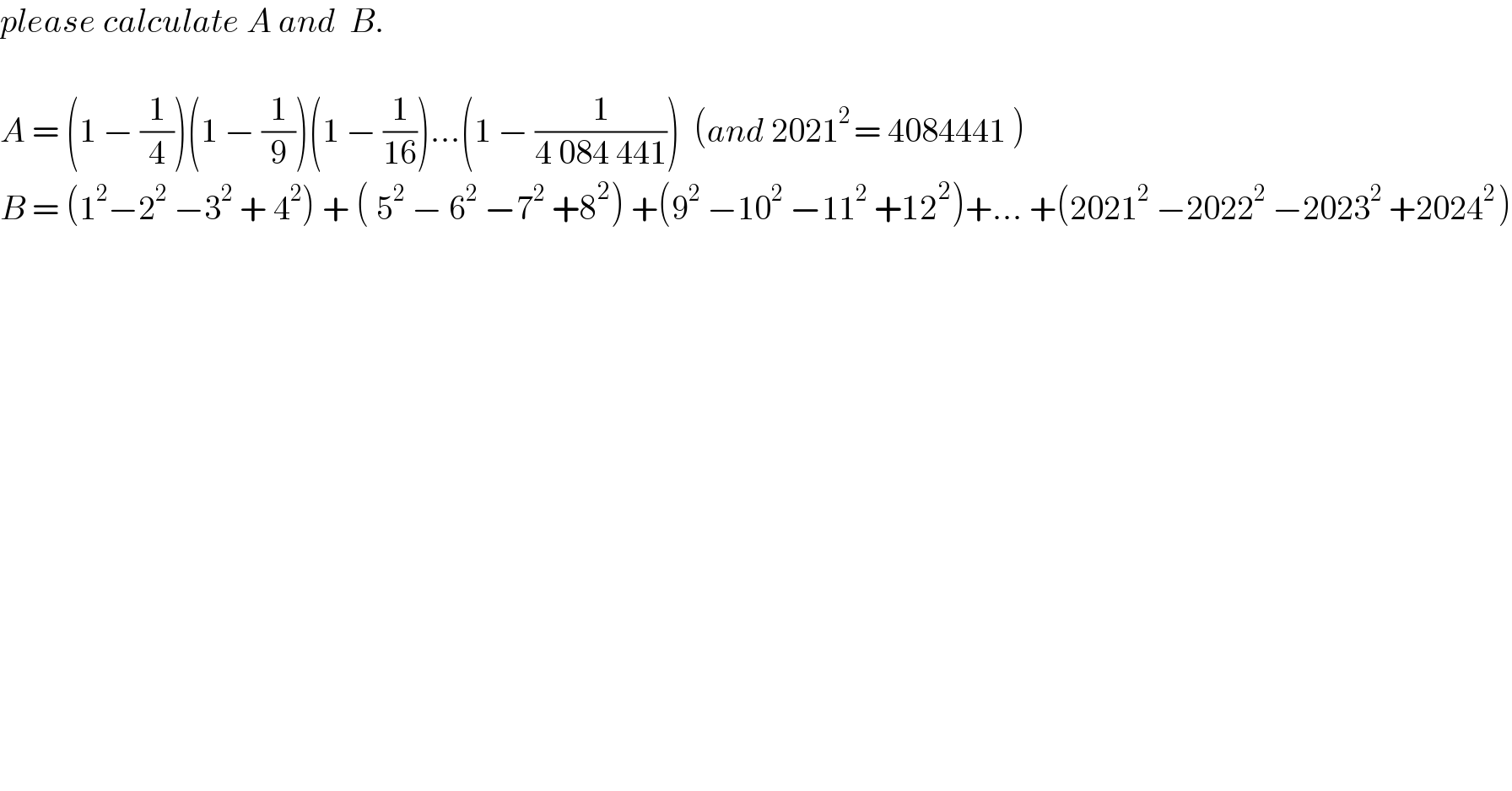
please calculate A and B. A = (1 − (1/4))(1 − (1/9))(1 − (1/(16)))...(1 − (1/(4 084 441))) (and 2021^(2 ) = 4084441 ) B = (1^2 −2^2 −3^2 + 4^2 ) + ( 5^2 − 6^2 −7^2 +8^2 ) +(9^2 −10^2 −11^2 +12^2 )+... +(2021^2 −2022^2 −2023^2 +2024^(2 ) )
$${please}\:{calculate}\:{A}\:{and}\:\:{B}. \\ $$$$ \\ $$$${A}\:=\:\left(\mathrm{1}\:−\:\frac{\mathrm{1}}{\mathrm{4}}\right)\left(\mathrm{1}\:−\:\frac{\mathrm{1}}{\mathrm{9}}\right)\left(\mathrm{1}\:−\:\frac{\mathrm{1}}{\mathrm{16}}\right)…\left(\mathrm{1}\:−\:\frac{\mathrm{1}}{\mathrm{4}\:\mathrm{084}\:\mathrm{441}}\right)\:\:\left({and}\:\mathrm{2021}^{\mathrm{2}\:} =\:\mathrm{4084441}\:\right) \\ $$$${B}\:=\:\left(\mathrm{1}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} \:−\mathrm{3}^{\mathrm{2}} \:+\:\mathrm{4}^{\mathrm{2}} \right)\:+\:\left(\:\mathrm{5}^{\mathrm{2}} \:−\:\mathrm{6}^{\mathrm{2}} \:−\mathrm{7}^{\mathrm{2}} \:+\mathrm{8}^{\mathrm{2}} \right)\:+\left(\mathrm{9}^{\mathrm{2}} \:−\mathrm{10}^{\mathrm{2}} \:−\mathrm{11}^{\mathrm{2}} \:+\mathrm{12}^{\mathrm{2}} \right)+…\:+\left(\mathrm{2021}^{\mathrm{2}} \:−\mathrm{2022}^{\mathrm{2}} \:−\mathrm{2023}^{\mathrm{2}} \:+\mathrm{2024}^{\mathrm{2}\:} \right) \\ $$
Commented by MJS_new last updated on 17/Dec/21
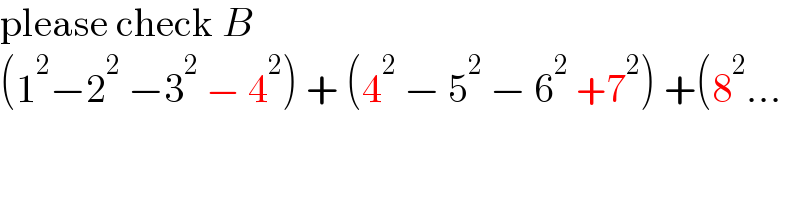
please check B (1^2 −2^2 −3^2 − 4^2 ) + (4^2 − 5^2 − 6^2 +7^2 ) +(8^2 ...
$$\mathrm{please}\:\mathrm{check}\:{B} \\ $$$$\left(\mathrm{1}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} \:−\mathrm{3}^{\mathrm{2}} \:−\:\mathrm{4}^{\mathrm{2}} \right)\:+\:\left(\mathrm{4}^{\mathrm{2}} \:−\:\mathrm{5}^{\mathrm{2}} \:−\:\mathrm{6}^{\mathrm{2}} \:+\mathrm{7}^{\mathrm{2}} \right)\:+\left(\mathrm{8}^{\mathrm{2}} …\right. \\ $$
Commented by stelor last updated on 17/Dec/21
sorrie i have mistaken.
$${sorrie}\:{i}\:{have}\:{mistaken}. \\ $$
Answered by MJS_new last updated on 17/Dec/21
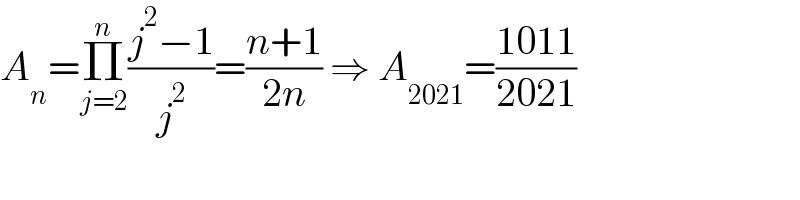
A_n =Π_(j=2) ^n ((j^2 −1)/j^2 )=((n+1)/(2n)) ⇒ A_(2021) =((1011)/(2021))
$${A}_{{n}} =\underset{{j}=\mathrm{2}} {\overset{{n}} {\prod}}\frac{{j}^{\mathrm{2}} −\mathrm{1}}{{j}^{\mathrm{2}} }=\frac{{n}+\mathrm{1}}{\mathrm{2}{n}}\:\Rightarrow\:{A}_{\mathrm{2021}} =\frac{\mathrm{1011}}{\mathrm{2021}} \\ $$
Answered by MohammadAzad last updated on 17/Dec/21
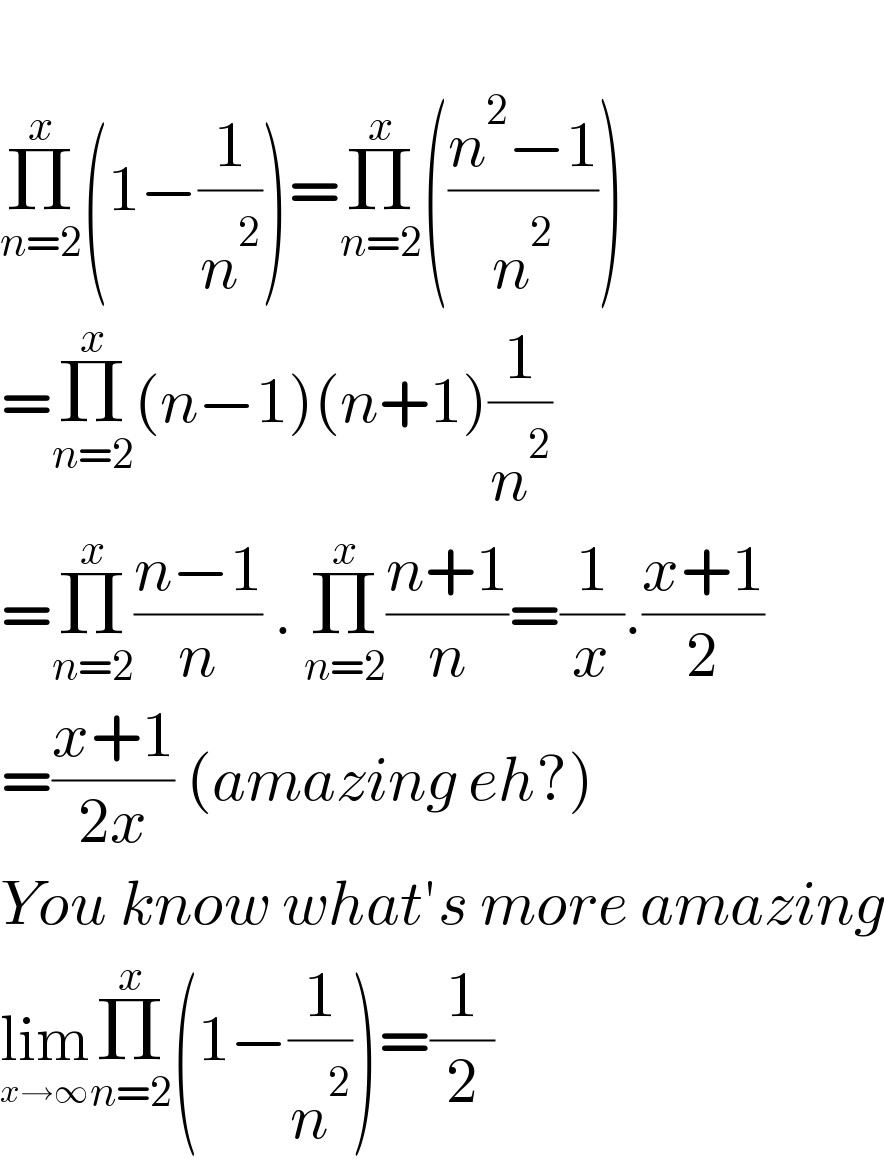
Π_(n=2) ^x (1−(1/n^2 ))=Π_(n=2) ^x (((n^2 −1)/n^2 )) =Π_(n=2) ^x (n−1)(n+1)(1/n^2 ) =Π_(n=2) ^x ((n−1)/n) . Π_(n=2) ^x ((n+1)/n)=(1/x).((x+1)/2) =((x+1)/(2x)) (amazing eh?) You know what′s more amazing lim_(x→∞) Π_(n=2) ^x (1−(1/n^2 ))=(1/2)
$$ \\ $$$$\underset{{n}=\mathrm{2}} {\overset{{x}} {\prod}}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)=\underset{{n}=\mathrm{2}} {\overset{{x}} {\prod}}\left(\frac{{n}^{\mathrm{2}} −\mathrm{1}}{{n}^{\mathrm{2}} }\right) \\ $$$$=\underset{{n}=\mathrm{2}} {\overset{{x}} {\prod}}\left({n}−\mathrm{1}\right)\left({n}+\mathrm{1}\right)\frac{\mathrm{1}}{{n}^{\mathrm{2}} } \\ $$$$=\underset{{n}=\mathrm{2}} {\overset{{x}} {\prod}}\frac{{n}−\mathrm{1}}{{n}}\:.\:\underset{{n}=\mathrm{2}} {\overset{{x}} {\prod}}\frac{{n}+\mathrm{1}}{{n}}=\frac{\mathrm{1}}{{x}}.\frac{{x}+\mathrm{1}}{\mathrm{2}} \\ $$$$=\frac{{x}+\mathrm{1}}{\mathrm{2}{x}}\:\left({amazing}\:{eh}?\right) \\ $$$${You}\:{know}\:{what}'{s}\:{more}\:{amazing} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\underset{{n}=\mathrm{2}} {\overset{{x}} {\prod}}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by MJS_new last updated on 17/Dec/21
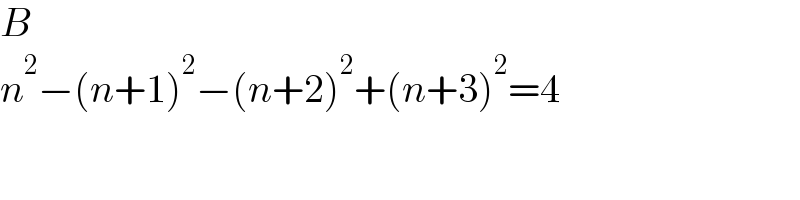
B n^2 −(n+1)^2 −(n+2)^2 +(n+3)^2 =4
$${B} \\ $$$${n}^{\mathrm{2}} −\left({n}+\mathrm{1}\right)^{\mathrm{2}} −\left({n}+\mathrm{2}\right)^{\mathrm{2}} +\left({n}+\mathrm{3}\right)^{\mathrm{2}} =\mathrm{4} \\ $$
Commented by stelor last updated on 17/Dec/21
okay. thanks 4×2021
$${okay}.\:{thanks} \\ $$$$\mathrm{4}×\mathrm{2021} \\ $$
Commented by MohammadAzad last updated on 17/Dec/21
Check your solution it is actually 4×((2024)/4)=2024 Σ_(i=0) ^((n−1)/4) [(4i+1)^2 −(4i+1+1)^2 −(4i+1+2)^2 +(4i+1+3)^2 ]=n+3
$${Check}\:{your}\:{solution}\:{it}\:{is}\: \\ $$$${actually}\:\mathrm{4}×\frac{\mathrm{2024}}{\mathrm{4}}=\mathrm{2024} \\ $$$$\underset{{i}=\mathrm{0}} {\overset{\frac{{n}−\mathrm{1}}{\mathrm{4}}} {\sum}}\left[\left(\mathrm{4}{i}+\mathrm{1}\right)^{\mathrm{2}} −\left(\mathrm{4}{i}+\mathrm{1}+\mathrm{1}\right)^{\mathrm{2}} −\left(\mathrm{4}{i}+\mathrm{1}+\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{4}{i}+\mathrm{1}+\mathrm{3}\right)^{\mathrm{2}} \right]={n}+\mathrm{3} \\ $$
Commented by MJS_new last updated on 17/Dec/21
you′re right
$$\mathrm{you}'\mathrm{re}\:\mathrm{right} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *