Question Number 52233 by de best last updated on 04/Jan/19
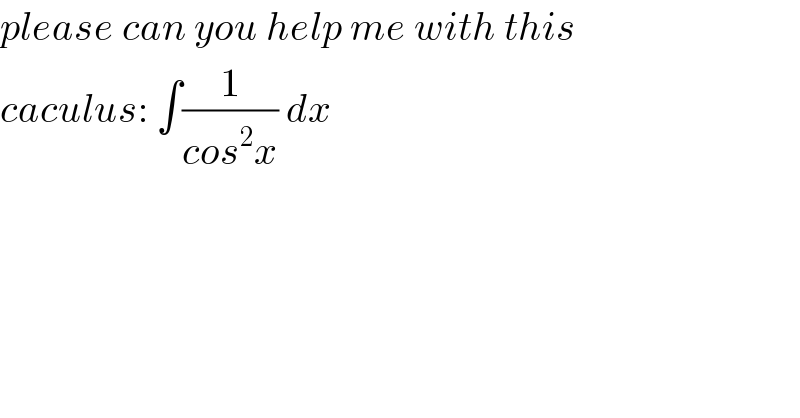
$${please}\:{can}\:{you}\:{help}\:{me}\:{with}\:{this}\: \\ $$$${caculus}:\:\int\frac{\mathrm{1}}{{cos}^{\mathrm{2}} {x}}\:{dx} \\ $$
Answered by MJS last updated on 04/Jan/19

$$\mathrm{this}\:\mathrm{is}\:\mathrm{a}\:\mathrm{standard}\:\mathrm{integral} \\ $$$${f}\left({x}\right)=\mathrm{tan}\:{x} \\ $$$${f}'\left({x}\right)=\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:{x}} \\ $$$$\Rightarrow\:\int\frac{{dx}}{\mathrm{cos}^{\mathrm{2}} \:{x}}=\mathrm{tan}\:{x}\:+{C} \\ $$
Answered by peter frank last updated on 04/Jan/19
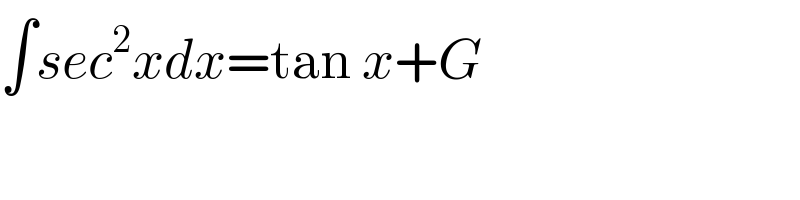
$$\int{sec}^{\mathrm{2}} {xdx}=\mathrm{tan}\:{x}+{G} \\ $$
Answered by peter frank last updated on 04/Jan/19
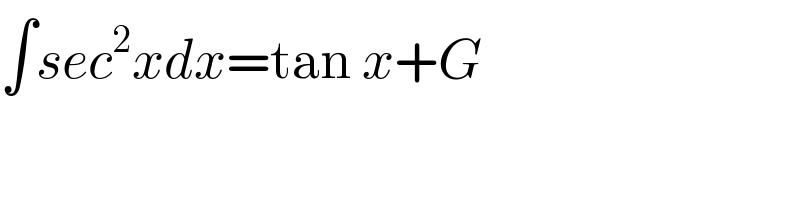
$$\int{sec}^{\mathrm{2}} {xdx}=\mathrm{tan}\:{x}+{G} \\ $$
